Пространственная система сил
7.1. Статические инварианты. Динамический винт
Ранее было установлено, что главный вектор системы сил, как угодно расположенных в пространстве,
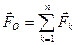 (7.1) не изменяется при перемене центра приведения. Главный же момент при этом не изменяется и для нового центра приведения определяется формулой
(7.1) не изменяется при перемене центра приведения. Главный же момент при этом не изменяется и для нового центра приведения определяется формулой
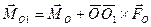 , (7.2) где
, (7.2) где 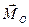 и
и 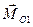 – главные моменты относительно центров приведения О и
– главные моменты относительно центров приведения О и 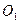 . Второе слагаемое в правой части формулы (7.2) представляет собой момент главного вектора, приложенного в центре приведения О, относительно нового центра приведения
. Второе слагаемое в правой части формулы (7.2) представляет собой момент главного вектора, приложенного в центре приведения О, относительно нового центра приведения 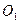 .
.
Умножим скалярно обе части равенства (7.2) на вектор 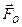 :
:
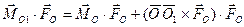 .
.
Так как вектор 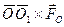 перпендикулярен вектору
перпендикулярен вектору 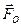 , то их скалярное произведение равно нулю. Следовательно,
, то их скалярное произведение равно нулю. Следовательно,
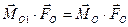 , (7.3) т.е. скалярное произведение главного вектора
, (7.3) т.е. скалярное произведение главного вектора 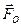 на главный момент не зависит от центра приведения.
на главный момент не зависит от центра приведения.
Таким образом, при перемене центра приведения не изменяются главный вектор и скалярное произведение главного вектора на главный момент. Говорят, что эти величины инвариантны относительно выбора центра приведения.
Первым статическим инвариантом называется главный вектор 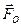 . В более узком смысле этого слова под первым инвариантом понимают квадрат модуля главного вектора
. В более узком смысле этого слова под первым инвариантом понимают квадрат модуля главного вектора
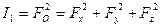 . (7.4)
. (7.4)
Вторым статическим инвариантом называется скалярное произведение главного вектора на главный момент:
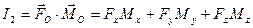 . (7.5)
. (7.5)
Из второго инварианта вытекает простое геометрическое следствие. Действительно, запишем равенство (7.3) в следующем виде:
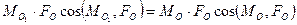 .
.
Если 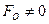 , то
, то
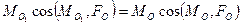 .
.
Каждое из этих произведений представляет собой проекцию главного момента на направление главного вектора. Следовательно, при перемене центра приведения проекция главного момента на направление главного вектора не изменяется. Заметим, что при 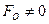 это следствие можно принять за определение второго инварианта.
это следствие можно принять за определение второго инварианта.
Так как проекция главного момента на направление главного вектора не изменяется при перемене центра приведения, то можно утверждать, что для центра приведения, в котором главный вектор и главный момент направлены по одной прямой, модуль главного момента будет минимальным. В этом случае модуль главного момента равен его проекции на направление главного вектора.
Очевидно, что проекция 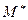 главного момента на направление главного вектора определяется равенством
главного момента на направление главного вектора определяется равенством
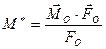 ,
,
или, принимая во внимание значения первого и второго инвариантов,
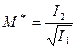 . (7.6)
. (7.6)
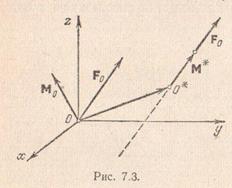
Совокупность силы и пары сил с моментом, коллинеарным силе, называется динамическим винтом или динамой. Так как плоскость действия пары перпендикулярна моменту пары, то динамический винт представляет собой совокупность силы и пары сил, действующей в плоскости, перпендикулярной силе. Различают правый и левый динамические винты. На рис. показан правый динамический винт, составленный из силы 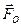 , равной главному вектору системы, и пары сил с моментом
, равной главному вектору системы, и пары сил с моментом 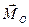 , равным главному моменту; на рис. показан левый винт, составленный из тех же элементов.
, равным главному моменту; на рис. показан левый винт, составленный из тех же элементов.
Может возникнуть вопрос, в каких случаях данную систему сил можно привести к динаме? На этот вопрос отвечает следующая теорема:
Если второй статический инвариант не равен нулю, то систему сил можно привести к динаме. На этот вопрос отвечает следующая теорема:
Если второй статический инвариант не равен нулю, то систему можно привести к динаме.
Пусть в произвольной точке О система приведена к силе, равной главному вектору 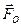 , и паре сил с моментом, равным главному моменту
, и паре сил с моментом, равным главному моменту 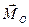 . Так как по условию теоремы
. Так как по условию теоремы 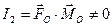 , то оба вектора,
, то оба вектора, 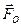 и
и 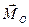 , не
, не 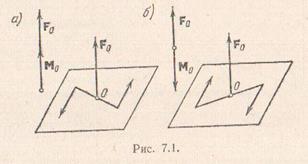 равны нулю и они не перпендикулярны между собой. Разложим главный момент на две составляющие: одну
равны нулю и они не перпендикулярны между собой. Разложим главный момент на две составляющие: одну 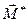 направим по главному вектору и другую
направим по главному вектору и другую 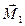 направим перпендикулярно главному вектору. Составляющая
направим перпендикулярно главному вектору. Составляющая 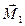 представляет собой момент пары сил, расположенной в плоскости, перпендикулярной вектору
представляет собой момент пары сил, расположенной в плоскости, перпендикулярной вектору 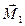 . Выберем силы
. Выберем силы 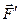 и
и 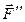 , составляющие эту
, составляющие эту 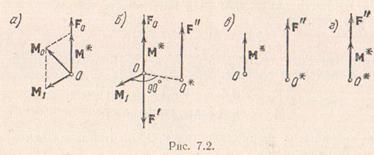 пару, равными по модулю главному вектору
пару, равными по модулю главному вектору 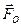 и приложим силу
и приложим силу 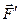 к центру приведения. Система сил (
к центру приведения. Система сил ( 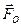 ,
, 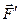 ), как эквивалентная нулю, может быть отброшена. Так как момент
), как эквивалентная нулю, может быть отброшена. Так как момент 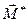 – вектор свободный, то его можно перенести из точки О в точку
– вектор свободный, то его можно перенести из точки О в точку 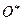 . Таким образом, заданная система сил приведена в точке
. Таким образом, заданная система сил приведена в точке 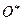 к силе
к силе 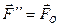 и паре сил с моментом
и паре сил с моментом 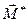 , расположенной в плоскости, перпендикулярной силе, т.е. мы получили динамический винт.
, расположенной в плоскости, перпендикулярной силе, т.е. мы получили динамический винт.
 Из формулы (7.6) видно, что положительному второму инварианту
Из формулы (7.6) видно, что положительному второму инварианту 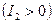 отвечает правый динамический винт, а отрицательному второму инварианту
отвечает правый динамический винт, а отрицательному второму инварианту 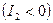 – левый динамический винт.
– левый динамический винт.
Точка 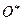 не единственная, где система сил приводится к динаме. В самом деле, силу можно переносить вдоль линии ее действия, момент же пары сил есть вектор свободный, следовательно, система сил может быть приведена к динаме во всех точках прямой, проходящей через точку
не единственная, где система сил приводится к динаме. В самом деле, силу можно переносить вдоль линии ее действия, момент же пары сил есть вектор свободный, следовательно, система сил может быть приведена к динаме во всех точках прямой, проходящей через точку 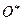 и являющейся линией действия силы
и являющейся линией действия силы 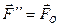 . Эта прямая называется центральной осью системы сил. Найдем теперь уравнение центральной оси.
. Эта прямая называется центральной осью системы сил. Найдем теперь уравнение центральной оси.
Пусть 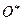 – точка центральной оси. Тогда для этой точки главный вектор и главный момент должны быть коллинеарны друг другу. На основании формулы (7.2) главный момент для точки
– точка центральной оси. Тогда для этой точки главный вектор и главный момент должны быть коллинеарны друг другу. На основании формулы (7.2) главный момент для точки 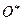 можно записать в виде
можно записать в виде
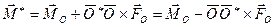 .
.
Условие коллинеарности главного вектора и главного момента для точки 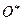 записывается следующим образом:
записывается следующим образом:
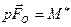 ,
,
где 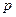 – параметр винта, имеющий размерность длины.
– параметр винта, имеющий размерность длины.
Таким образом,
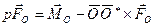 . (7.7)
. (7.7)
Пусть 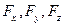 и
и 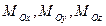 – соответственно проекции главного вектора и главного момента на оси х, у и z; тогда
– соответственно проекции главного вектора и главного момента на оси х, у и z; тогда
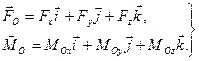
Пусть координаты какой-либо точки 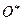 центральной оси будут х, у, z, следовательно,
центральной оси будут х, у, z, следовательно,
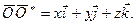
Подставляя соответствующие выражения в соотношение (7.7), получим
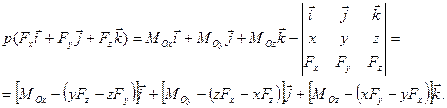
Приравнивая коэффициенты при единичных векторах 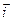 ,
, 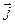 и
и 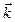 , имеем
, имеем
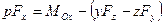 ,
,
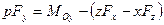 ,
,
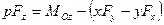 .
.
Следовательно,
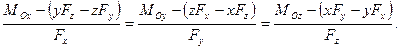 (7.8) Это и есть искомые уравнения центральной оси.
(7.8) Это и есть искомые уравнения центральной оси.
