Системы уравнений и неравенств с одним неизвестным
Пример 5. Решить систему уравнений
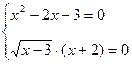 .
.
Решение. Первое уравнение – квадратное, поэтому его корни вычисляются по формуле
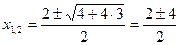 или x1 = 3, x2 = –1.
или x1 = 3, x2 = –1.
При решении второго уравнения надо указать вначале его область определения: x ³ 3. Далее, приравняв каждый из множителей нулю и решив получившиеся уравнения, будем иметь x1 = 3,
x2 = –2. Число x2 = –2 не принадлежит области определения [3,+¥) и является посторонним корнем. Следовательно, система уравнений имеет единственное решение: {3}.
Пример 6. Решить систему неравенств
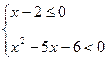 .
.
Решение. Первое неравенство линейное и его множество решений имеет вид (–¥, 2]. Второе неравенство – квадратное, его можно решить методом интервалов. Для этого разложим квадратный трехчлен в произведение:
x2 – 5x – 6 = (x + 1)(x – 6).
Далее числа x1 = –1 и x2 = 6 (заметим, что это – корни соответствующего уравнения) нанесем на числовую прямую и определим знаки квадратного трехчлена – левой части неравенства в каждом из полученных интервалов. Имеем
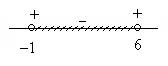
Заштрихуем те интервалы, в которых квадратный трехчлен имеет нужный нам знак (знак –). (Числа x1 = –1 и x2 = 6 отмечены незакрашенными кружочками, так как неравенство строгое.) Таким образом, множество решений второго неравенства (–1, 6). Чтобы получить решения системы неравенств, найдем пересечение двух множеств: (–¥, 2] Ç (–1, 6) = (–1, 2]. Геометрически это можно изобразить так:
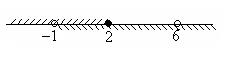
Пересечением множеств является множество точек, на котором штриховки накладываются друг на друга.
Учитывая рассмотренные примеры 5 и 6, можно сделать один вывод. Множество решений системы уравнений или неравенств представляет собой пересечение множеств решений каждого из уравнений или неравенств, входящих в эту систему.
Иногда в процессе решения системы уравнений или неравенств получается некоторая совокупность других систем, к которым приводится данная система. В таких случаях множество решений исходной системы является объединением множеств решений каждой системы, входящей в эту совокупность. Разберем один пример.
Пример 7. Решить систему неравенств
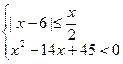 .
.
Решение. Раскрывая модуль в первом неравенстве системы, получим два случая: 1) 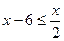 при x – 6 ³ 0 и 2)
при x – 6 ³ 0 и 2) 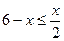 при x – 6 < 0. Принимая во внимание второе неравенство исходной системы, приходим к совокупности двух систем:
при x – 6 < 0. Принимая во внимание второе неравенство исходной системы, приходим к совокупности двух систем:
1) 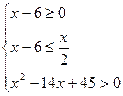 или 2)
или 2) 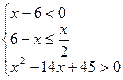 .
.
Вначале решим первую систему из этой совокупности. Здесь первое и второе неравенства линейные и имеют решения, соответственно, [6, +¥) и (–¥, 12]. Третье неравенство квадратное. Решая его методом интервалов (так же, как и второе неравенство в примере 6), получаем
(–¥, 5) È (9, +¥). Множество решений системы есть пересечение трех множеств:
[6, +¥) Ç (–¥, 12] Ç ((–¥, 5) È (9, +¥)).
Найдем пересечение первого и второго множества:
[6, +¥) Ç (–¥, 12] = [6, 12].
Используя распределительный закон пересечения относительно объединения (см. § 4), будем иметь
[6, 12] Ç ((–¥, 5) È (9, +¥)) = ([6, 12] Ç (–¥, 5)) È ([6, 12] Ç (9, +¥)) = Æ È (9, 12] = (9, 12].
Теперь решим вторую систему из совокупности. Проводя аналогичные рассуждения, как и в первом случае, получим три множества: (–¥, 6), [4, +¥) и (–¥, 5) È (9, +¥). Найдем их пересе-чение: (–¥, 6) Ç [4, +¥) = [4, 6); [4, 6) Ç ((–¥, 5) È (9, +¥)) = ([4, 6) Ç (–¥, 5)) È ([4, 6) Ç (9, +¥)) =
= [4, 5) È Æ = [4, 5).
Множество решений исходной системы является объединением множеств (9, 12] и [4, 5),
то есть [4, 5) È (9, 12].
