Декартовы координаты на прямой и на плоскости
А. П. Чеголин, А.В. Гиль
Учебное пособие по высшей математике для студентов естественных
Факультетов.
Модуль 2. аналитическая геометрия
(учебное пособие)
Ростов-на-Дону
| Чеголин А.П., Гиль А.В. | |
| Учебное пособие по высшей математике для студентов естественных факультетов. Модуль 2. Аналитическая геометрия: учебное пособие. Ростов-на-Дону, 2008. 89с. |
Настоящее учебно-методическое пособие предназначено для студентов первого курса естественных факультетов Южного федерального университета. Его цель – помочь студентам овладеть навыками самостоятельной работы при изучении модуля 2 «Аналитическая геометрия» курса «Математика».
Учебное пособие составлено в соответствии с действующей программой. Оно содержит: лекционный материал по соответствующему модулю с примерами решения наиболее характерных задач.
Оглавление
Введение ……………………………………………………………………….5
1. Декартовы координаты на прямой и на плоскости...…………………….6
2. Декартовы координаты в пространстве…...……………………………...9
3. Полярные координаты на плоскости. Цилиндрические и
сферические координаты в пространстве.……………………….……...11
4. Простейшие задачи в декартовых координатах………………………...14
5. Геометрические векторы. Основные понятия. Линейные операции
над векторами……………..………………………………………………17
6. Линейная зависимость и независимость геометрических векторов..…21
7. Базис. Координаты вектора………..……………………….…………….25
8. Скалярное произведение....………………….…………………………...29
9. Векторное произведение………………………….……………………...32
10. Смешанное произведение векторов...………..…………………………38
11. Уравнение линии на плоскости………………….……………………...42
12. Общее уравнение прямой на плоскости………………………………..43
13. Каноническое уравнение и параметрические уравнения прямой
на плоскости…………………………………………………………………..46
14. Уравнение прямой с угловым коэффициентом. Угол между
прямыми на плоскости……………………………………………………….47
15. Нормальное уравнение прямой на плоскости.…………………………51
16. Кривые второго порядка…………………………………………………54
17. Окружность. Эллипс………………………...…………………………...56
18. Гипербола…………………………………………....……………………63
19. Парабола……………………………………………………………….….71
20. Уравнение поверхности в пространстве………………………………..74
21. Общее уравнение плоскости в пространстве…….………………...…..74
22. Уравнение плоскости, проходящей через три данные точки.
Нормальное уравнение плоскости………………………………….……….79
23. Уравнение линии в пространстве. Прямая линия в пространстве.…...83
24. Поверхности второго порядка…………………………..………………86
Тесты………………………..……………………………………………..89
Ответы на вопросы тестов………………………………………………99
Задачи…………………………………………………………………….99
Литература ………………………………………………………………106
Введение.
Настоящее учебное пособие содержит: лекционный материал по модулю 2 «Аналитическая геометрия» курса «Математика», а также блок задач и вопросов для самоконтроля по рассматриваемому материалу.
Рассматриваемый здесь раздел имеет самостоятельное научное значение. Основная цель этого раздела - изучение свойств геометрических объектов при помощи аналитического метода. Особое внимание уделено различным системам координат на плоскости и в пространстве, уравнениям линий на плоскости и поверхностей в пространстве. Рассматриваемый здесь материал актуален не только с точки зрения логических принципов построения геометрии, но и для понимания ряда разделов современной физиики и химии, особенно здесь стоит отметить потребности теоретической механики. Кроме того, овладение материалом этого раздела необходимо при изучении многих последующих разделов высшей математики, таких как математический анализ, дифференциальные уравнения и уравнения математической физики.
В пособии используются классические математические методы. Для определения основных геометрических объектов часто используется аксиоматический метод, в развитии которого большая заслуга принадлежит Давиду Гильберту. Аксиоматический метод закладывает фундамент и для лежащего в основе аналитической геометрии метода координат, впервые систематически примененный Рене Декартом.
Декартовы координаты на прямой и на плоскости.
Задать координаты на плоскости означает установить правило, по которому каждому числу (на прямой) или набору чисел (на плоскости или пространстве) ставится в соответствие единственная точка.
Введем декартовы координаты на оси. Прямую линию с указанным на ней направлением будем называть осью. Отрезок на оси называется направленным, если указано, какая из его граничных точек является началом и какая – концом. Направленный отрезок с началом в точке 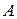 и концом в точке
и концом в точке 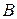 будем обозначать
будем обозначать 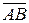 . Нулевым называется направленный отрезок, у которых начало и конец совпадают. Величиной направленного отрезка
. Нулевым называется направленный отрезок, у которых начало и конец совпадают. Величиной направленного отрезка 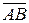 называется число, равное длине этого отрезка, взятой со знаком плюс, если направление
называется число, равное длине этого отрезка, взятой со знаком плюс, если направление 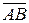 совпадает с направлением оси, и со знаком минус, если направление
совпадает с направлением оси, и со знаком минус, если направление 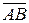 противоположно направлению оси. Величину направленного отрезка
противоположно направлению оси. Величину направленного отрезка 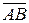 будем обозначать
будем обозначать 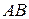 .
.
Выберем на оси некоторую точку 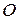 , которую будем называть началом координат. Кроме того, укажем единицу масштаба.
, которую будем называть началом координат. Кроме того, укажем единицу масштаба.
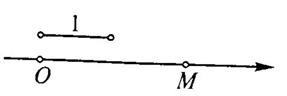 Рассмотрим произвольную точку
Рассмотрим произвольную точку  на оси. Декартовой координатой
на оси. Декартовой координатой 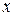 точки
точки  называется величина направленного отрезка
называется величина направленного отрезка 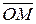 . Действительно, значение
. Действительно, значение 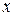 однозначно определяет положение точки
однозначно определяет положение точки  на прямой. Тот факт, что точка
на прямой. Тот факт, что точка  имеет координату
имеет координату 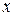 , обозначается:
, обозначается: 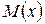 .
.
Теорема.Пусть 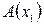 ,
, 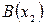 - две точки на оси. Тогда величина направленного отрезка
- две точки на оси. Тогда величина направленного отрезка 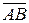 равна
равна 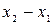 .
.
Доказательство. Очевидно, что справедливо равенство:
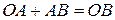 .
.
Так как 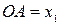 ,
, 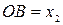 , то
, то
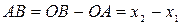 . ■
. ■
Следствие.Расстояние между точками 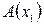 и
и 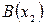 определяется формулой:
определяется формулой:
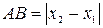 .
.
 Введем прямоугольные декартовы координаты на плоскости. Выберем на плоскости некоторую точку
Введем прямоугольные декартовы координаты на плоскости. Выберем на плоскости некоторую точку 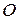 , которую будем называть началом координат. Кроме того, укажем единицу масштаба. Через начало координат проводим две взаимно перпендикулярные оси, которые будем называть координатными. Одна из них называется осью абсцисс и обозначается
, которую будем называть началом координат. Кроме того, укажем единицу масштаба. Через начало координат проводим две взаимно перпендикулярные оси, которые будем называть координатными. Одна из них называется осью абсцисс и обозначается 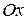 , вторая – называется осью ординат и обозначается
, вторая – называется осью ординат и обозначается 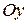 . Направления этих осей выбираются таким образом, чтобы кратчайший поворот от положительного направления оси абсцисс до положительного направления оси ординат осуществлялся против часовой стрелки.
. Направления этих осей выбираются таким образом, чтобы кратчайший поворот от положительного направления оси абсцисс до положительного направления оси ординат осуществлялся против часовой стрелки.
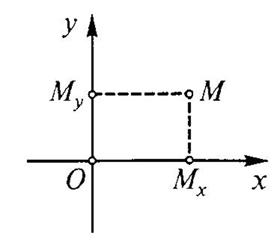
Рассмотрим произвольную точку  на плоскости. Спроектируем эту точку на координатные оси. В результате получим: точка
на плоскости. Спроектируем эту точку на координатные оси. В результате получим: точка 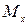 - проекция точки
- проекция точки  на ось
на ось 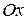 , точка
, точка 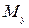 - проекция точки
- проекция точки  на ось
на ось 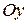 . Абсциссой
. Абсциссой 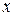 точки
точки  называется величина направленного отрезка
называется величина направленного отрезка 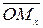 , а ординатой
, а ординатой 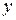 - величина направленного отрезка
- величина направленного отрезка 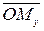 . Абсцисса
. Абсцисса 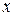 и ордината
и ордината 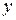 составляют декартовы координаты точки на плоскости. Действительно, упорядоченная пара
составляют декартовы координаты точки на плоскости. Действительно, упорядоченная пара 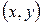 однозначно определяет положение точки на плоскости. Тот факт, что точка
однозначно определяет положение точки на плоскости. Тот факт, что точка  имеет абсциссу
имеет абсциссу 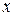 и ординату
и ординату 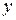 , обозначается:
, обозначается: 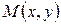 . Сама плоскость после введения декартовой системы координат обозначается:
. Сама плоскость после введения декартовой системы координат обозначается: 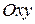 .
.
Рассмотрим возможные преобразования декартовой системы координат на плоскости.
Параллельным переносом прямоугольной декартовой системы координат на плоскости называется такое ее преобразование, при котором не меняются направления осей, а начало координат 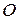 перемещается в новую точку
перемещается в новую точку 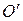 на плоскости.
на плоскости.
Пусть в исходной системе координат точка 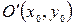 . Тогда очевидно, что для произвольной точки
. Тогда очевидно, что для произвольной точки  на плоскости координаты
на плоскости координаты 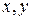 в исходной системе координат и координаты
в исходной системе координат и координаты 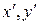 в новой системе связаны равенствами:
в новой системе связаны равенствами:
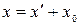 ,
,
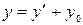 .
.
Поворотом прямоугольной системы координат на плоскости называется такое ее преобразование, при котором начало координат 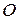 остается без изменения, а координатные оси поворачиваются на один и тот же угол
остается без изменения, а координатные оси поворачиваются на один и тот же угол 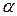 .
.
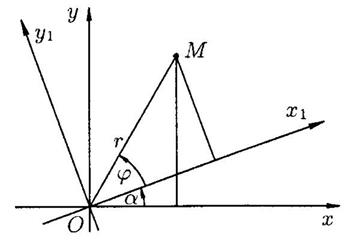 Пусть точка
Пусть точка  на плоскости
на плоскости 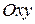 имеет координаты
имеет координаты 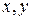 , а в вистеме
, а в вистеме 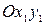 , полученной поворотом на угол
, полученной поворотом на угол 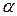 , координаты этой точки равны
, координаты этой точки равны 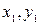 . Пусть
. Пусть 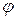 - угол от положительного направления оси
- угол от положительного направления оси 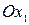 до направленного отрезка
до направленного отрезка 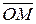 , и
, и 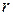 - длина этого отрезка. Тогда из рисунка видно, что
- длина этого отрезка. Тогда из рисунка видно, что
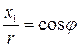 ,
, 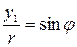 ,
, 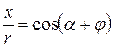 ,
, 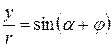 .
.
Следовательно,
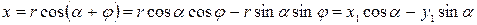 ,
,
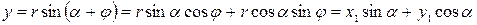 .
.
Таким образом, переход от старой системы координат к новой описывается формулами:
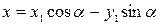 ,
,
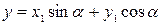 .
.
Для того, чтобы выразить координаты в новой системе через координаты в старой системе, достаточно представить, что старая система получается из новой поворотом на угол 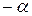 . В результате получим:
. В результате получим:
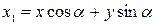 ,
,
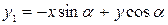 .
.
