Векторный базис на плоскости и в пространстве
В случае неколлинеарности двух векторов аи b любой третий вектор с, компланарный с, а и b, как следует из рисунка 16, можно однозначно представить в виде
с= xa + yb, (1)
где x, y Î R.
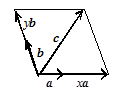 |
Рисунок 16
Линейной комбинацией векторов а1, а2, …, аn называется вектор
а = х1а1 + х2а2 + … + хnаn, (2)
где х1, х2, …, хn – действительные числа, называемые коэффициентами линейной комбинации.
Если вектор а представлен в виде линейной комбинации (2), то будем говорить, что а разложен по векторам а1, а2, …, аn. В частности, на основании равенства (1) мы можем сказать, что вектор сразложен по векторам aи b.
Векторным базисом на плоскости называется любая упорядоченная пара (е1; е2) неколлинеарных векторов этой плоскости.
Можно заметить, что каждая плоскость содержит бесконечное мно-
жество базисов.
По аналогии с выводом, сделанным из рисунка 16, можно утверждать, что любой вектор а некоторой плоскости можно однозначно представить в виде линейной комбинации базисных векторов е1, е2 этой плоскости, т. е.
а = хе1 + уе2. (3)
Из этого следует вывод: если на плоскости выбран базис (е1; е2), то каждому вектору а этой плоскости ставится в соответствие един-
ственная упорядоченная пара действительных чисел х, y и, обратно, каждой упорядоченной паре чисел х, y поставлен в соответствие един-
ственный вектор а, который определяется равенством (3). При этом числа х, y мы будем называть координатами вектора а в базисе (е1; е2).
Ортонормированным базисом называется такой базис (i; j), который удовлетворяет условиям: i^ j, | i| = | j| = 1, т. е. векторы i, j этого базиса единичны и взаимно перпендикулярны. В этом случае, если
а = (х; y) в базисе (i; j), то а = хi + yj и наоборот. Числа х, y называются координатами вектора а в базисе (i; j).
Два вектора а = (x1; y1), b = (x2; y2) образуют базис на плоскости тогда и только тогда, когда определитель второго порядка, составленный из координат этих векторов, отличен от нуля.
Пример 1. Разложение вектора а= (–3; 7) по базису (i; j) имеет вид а= –3i+ 7j. Если же а = 2i – 3j, то координатами вектора а в базисе
(i; j) будут (2; –3).
Чтобы найти координаты вектора 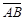 , надо от координат конца В этого вектора вычесть координаты его начала А, т. е. если A(x1; y1), B(x2; y2), то
, надо от координат конца В этого вектора вычесть координаты его начала А, т. е. если A(x1; y1), B(x2; y2), то 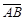 =
= 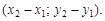
Пример 2.Пусть А(3; –5), В(–2; 3), тогда 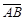 = (–2 – 3; 3 – (–5)) =
= (–2 – 3; 3 – (–5)) =
= (–5; 8).
Тест 1. Найти координаты вектора 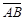 , если А(3; 4), В(5; 7):
, если А(3; 4), В(5; 7):
1) (2; 4);
2) (2; 7);
3) (2; 3);
4) (3; 3);
5) (3; 3).
Пример 3. Пара векторов а = (1; 2), b = (–3; 5) образует базис на плоскости, так как определитель, составленный из координат, не равен 0: 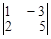 = 1 × 5 – 2 × (–3) = 11
= 1 × 5 – 2 × (–3) = 11 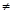 0.
0.
Тест 2. Определить, какие из следующих пар векторов не образуют базис на плоскости:
1) (3; 4), (2; 1);
2) (–2; 1), (2; 5);
3) (–4; 5), (1; 4);
4) (1; 2), (3; 6);
5) (7; 1), (2; 4).
Векторным базисом пространства называется любая упорядоченная тройка (ℓ1, ℓ2, ℓ3) некомпланарных векторов этого пространства.
Скалярное произведение векторов
Скалярным произведением a × b двух ненулевых векторов a и b называется число, равное произведению длин этих векторов на косинус угла между ними. В случае равенства нулю хотя бы одного из этих векторов скалярное произведение равно нулю. Таким образом, по определению имеем
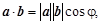 (4)
(4)
где j – угол между векторами a и b.
Скалярное произведение векторов a, b обозначается также при помощи символов ab.
Знак скалярного произведения определяется величиной j:
если 0 £ j £ 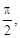 то a × b ³ 0,
то a × b ³ 0,
если же 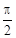 < j £ p, то a × b < 0.
< j £ p, то a × b < 0.
Скалярное произведение определяется только для двух векторов.
