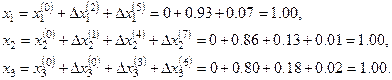Приведение исходной системы к виду, удобному для применения сходящегося итерационного процесса
Метод простых итераций для решения систем линейных алгебраических уравнений.
Пусть дана система линейных алгебраических уравнений вида (4.1).
Предположим, что диагональные элементы матрицы 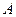 не равны нулю, т.е.
не равны нулю, т.е. 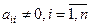 (в случае равенства одного или нескольких из них нулю, с помощью перестановки уравнений или других эквивалентных преобразований можно добиться, чтобы они были отличны от нуля). Разделив
(в случае равенства одного или нескольких из них нулю, с помощью перестановки уравнений или других эквивалентных преобразований можно добиться, чтобы они были отличны от нуля). Разделив 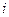 -ое уравнение системы на
-ое уравнение системы на 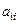 , получим:
, получим:
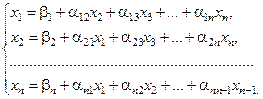 (4.4)
(4.4)
где коэффициенты 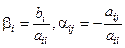 при
при 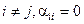 .
.
Введем обозначения:
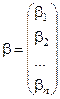 ,
, 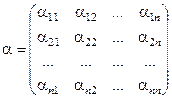 (4.5)
(4.5)
Тогда система (4.4) примет вид:
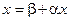 (4.6)
(4.6)
Систему (4.6) будем решать методом последовательных приближений. Выбираем начальное приближение 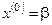 ; далее вычисляем следующие приближения:
; далее вычисляем следующие приближения:
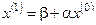 ,
, 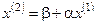 ,…,
,…, 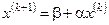 , … (4.7)
, … (4.7)
Если последовательность приближений 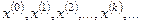 является сходящейся, т.е. у нее существует предел
является сходящейся, т.е. у нее существует предел 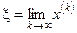 , то этот предел
, то этот предел 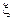 является решением системы (4.6). Действительно,
является решением системы (4.6). Действительно,
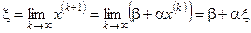 .
.
Получили 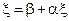 , т.е.
, т.е. 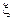 – является решением системы (4.6), а система (4.6) получена из системы (4.1), следовательно,
– является решением системы (4.6), а система (4.6) получена из системы (4.1), следовательно, 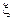 будет являться решением исходной системы (4.1).
будет являться решением исходной системы (4.1).
Теорема 4.1(достаточное условие сходимости итерационного процесса).
Если для приведенной системы 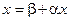 выполнено хотя бы одно из условий:
выполнено хотя бы одно из условий:
а) 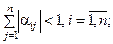
б) 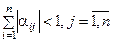 ,
,
то процесс итерации, заданный формулой 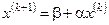 , сходится к единственному решению этой системы, независимо от выбора начального приближения.
, сходится к единственному решению этой системы, независимо от выбора начального приближения.
В частности процесс итерации заведомо сходится, если элементы 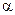 приведенной системы (4.4) удовлетворяют неравенству
приведенной системы (4.4) удовлетворяют неравенству 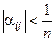 , где
, где 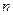 - число неизвестных системы.
- число неизвестных системы.
Следствие.
Для исходной системы (4.1) итерационный процесс сходится, если выполнены неравенства 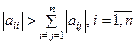 (то есть модули диагональных коэффициентов для каждого уравнения системы больше суммы модулей всех остальных коэффициентов, не считая свободных членов).
(то есть модули диагональных коэффициентов для каждого уравнения системы больше суммы модулей всех остальных коэффициентов, не считая свободных членов).
Теорема 4.2 (необходимое и достаточное условие сходимости процесса итерации для системы линейных уравнений).
Для сходимости процесса итераций: 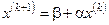 при любом выборе начального приближения
при любом выборе начального приближения 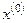 и любом свободном члене
и любом свободном члене 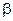 необходимо и достаточно, чтобы собственные значения матрицы
необходимо и достаточно, чтобы собственные значения матрицы 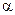 (т.е. корни характеристического уравнения
(т.е. корни характеристического уравнения 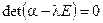 ) были по модулю меньше единицы.
) были по модулю меньше единицы.
Приведение исходной системы к виду, удобному для применения сходящегося итерационного процесса.
Теорема сходимости итерационного процесса накладывает жесткие условия на коэффициенты системы (4.3). Однако, если 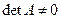 , то с помощью элементарных преобразований системы (4.3) ее можно заменить эквивалентной системой
, то с помощью элементарных преобразований системы (4.3) ее можно заменить эквивалентной системой 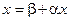 , такой, что условия теоремы сходимости будут выполнены.
, такой, что условия теоремы сходимости будут выполнены.
Умножим левую и правую часть соотношения (4.3) слева на матрицу 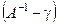 , где
, где 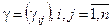 - матрица с малыми по модулю элементами.
- матрица с малыми по модулю элементами.
Проведем преобразования:
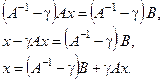
Если обозначить 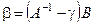 ,
, 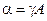 , то получим
, то получим 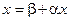 .
.
Если элементы матрицы 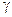 достаточно малы по модулю, т.е. ú
достаточно малы по модулю, т.е. ú 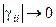 , то элементы матрицы
, то элементы матрицы 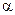 будут удовлетворять достаточному условию сходимости итерационного процесса.
будут удовлетворять достаточному условию сходимости итерационного процесса.
Итерационный процесс заканчивается, если для двух приближений 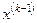 и
и 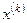 выполнено условие
выполнено условие 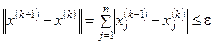 , где
, где 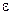 - заданная точность.
- заданная точность.
§4.2. Метод Зейделя.
Метод Зейделя представляет собой некоторую модификацию метода простых итераций. Основная его идея состоит в том, что при вычислении 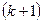 -го приближения неизвестной
-го приближения неизвестной 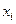 учитываются уже вычисленные ранее
учитываются уже вычисленные ранее 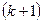 -е приближения неизвестных
-е приближения неизвестных 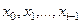 . Т.е. найденное
. Т.е. найденное 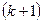 -е приближение сразу же используется для получения
-е приближение сразу же используется для получения 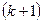 -го приближения последующих координат (Рис.4.1).
-го приближения последующих координат (Рис.4.1).
Предполагая, что 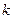 -е приближения
-е приближения 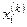 корней системы (4.4) известны,
корней системы (4.4) известны, 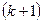 -е приближения корней будут находиться по следующим итерационным формулам метода Зейделя:
-е приближения корней будут находиться по следующим итерационным формулам метода Зейделя:
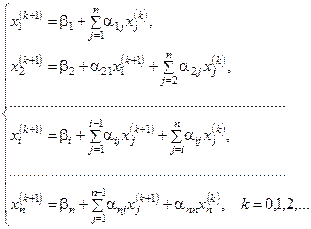 . (4.8)
. (4.8)
Теорема 4.3(достаточное условие сходимости метода Зейделя).
Если для приведенной системы 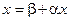 выполнено хотя бы одно из условий:
выполнено хотя бы одно из условий:
1) 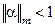 , где
, где 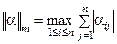 ;
;
2) 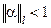 , где
, где 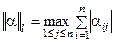 ;
;
3) 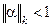 , где
, где 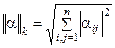 ,
,
то процесс Зейделя сходится к единственному решению системы при любом выборе начального вектора.
Запишем систему (4.8) в сокращенном виде:
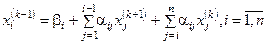 (4.9)
(4.9)
Введем обозначения:
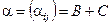 ,
,
где
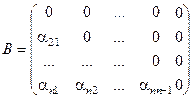 ,
, 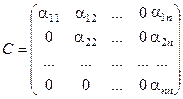 .
.
Тогда формулу (4.9) можем переписать в матричном виде:
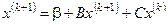 , (4.10)
, (4.10)
где
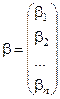 ,
, 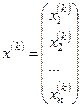 ,
, 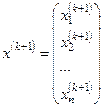 .
.
Теорема 4.4(необходимые и достаточные условия сходимости метода Зейделя).
Для сходимости процесса Зейделя, заданного формулой (4.9), для приведенной системы линейных уравнений (4.4) при любом выборе свободного члена 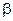 и начального вектора
и начального вектора 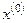 необходимо и достаточно, чтобы все корни
необходимо и достаточно, чтобы все корни 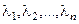 уравнения
уравнения 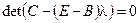 были по модулю меньше единицы.
были по модулю меньше единицы.
Пример 4.1. Построить рабочие формулы метода простых итераций и метода Зейделя для численного решения СЛАУ вида:
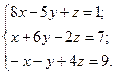 (4.11)
(4.11)
Решение.
Заметим, что система (4.11) имеет точное решение 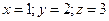 .
.
Из системы (4.11) видно, что модули диагональных коэффициентов в каждом уравнении отличны от нуля и больше суммы модулей всех остальных коэффициентов, не считая столбца свободных членов. Тогда, разделим каждое уравнение системы (4.11) на соответствующий диагональный коэффициент, сформируем столбец  в левой части и перенесем остальные слагаемые в правую часть и получим рабочие формулы метода простых итераций вида:
в левой части и перенесем остальные слагаемые в правую часть и получим рабочие формулы метода простых итераций вида:
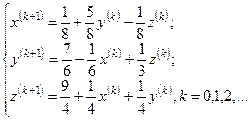
Начальное приближение обычно выбирают равным столбцу свободных членов преобразованной системы 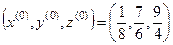 .
.
Рабочие формулы метода Зейделя запишутся так:
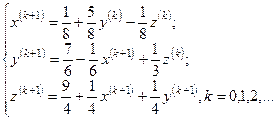
§4.3. Метод релаксации.
Рассмотрим систему линейных алгебраических уравнений (4.1), в которой 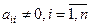 .
.
Сделаем преобразования: для этого свободные члены перенесем в левую часть и каждое 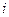 -тое уравнение поделим на
-тое уравнение поделим на 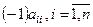 . Таким образом, получим систему, удобную для релаксации:
. Таким образом, получим систему, удобную для релаксации:
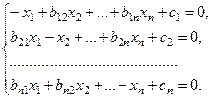 (4.12)
(4.12)
где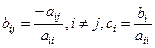 .
.
Введем понятие невязки для приближенного решения 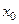 .
.
Пусть дана система 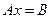 , тогда точное решение
, тогда точное решение 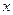 можно записать в виде
можно записать в виде 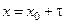 , где
, где 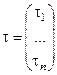 -правка корня
-правка корня 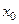 . Подставим
. Подставим 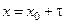 в систему, получим
в систему, получим
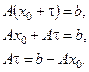
Введем обозначение 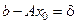 . Тогда
. Тогда  . Выражение
. Выражение 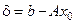 называется невязкой для приближенного решения
называется невязкой для приближенного решения 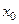 .
.
Пусть задано начальное приближение системы (4.12):
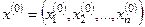 .
.
Подставим данное приближение в систему (4.12) и получим невязки  :
:
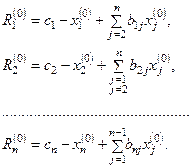 (4.13)
(4.13)
Если одной из неизвестных 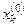 дать приращение
дать приращение 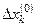 , то соответствующая невязка
, то соответствующая невязка 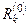 уменьшится на величину
уменьшится на величину 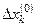 , а все остальные невязки
, а все остальные невязки 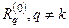 изменятся на величину
изменятся на величину 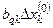 . Чтобы обратить очередную невязку
. Чтобы обратить очередную невязку 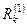 в нуль, нужно величине
в нуль, нужно величине 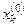 дать приращение
дать приращение 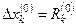 , следовательно,
, следовательно, 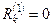 , а остальные невязки будут равны
, а остальные невязки будут равны
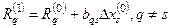 .
.
Метод релаксации (метод ослабления) заключается в том, что на каждом шаге обращают в нуль максимальную по модулю невязку путем изменения значения соответствующей компоненты приближения. Процесс заканчивается, когда все невязки последней преобразованной системы будут равны нулю с заданной точностью.
Пример 4.2. Решить систему методом релаксации, производя вычисления с двумя десятичными знаками.
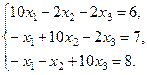 (4.14)
(4.14)
Решение.
Приведем систему (4.14) к виду, удобному для релаксации
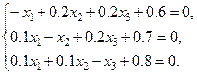 (4.15)
(4.15)
В качестве начального приближения выбираем
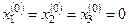 .
.
Находим соответствующие невязки: 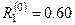 ,
, 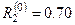 ,
, 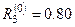 . Выбираем максимальную невязку и полагаем
. Выбираем максимальную невязку и полагаем 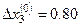 , тогда
, тогда
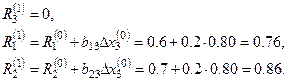
Опять выбираем максимальную невязку и полагаем 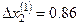 , тогда
, тогда
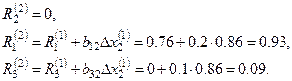
Далее 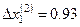 и
и
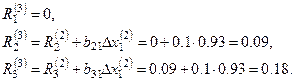
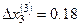 ,
,
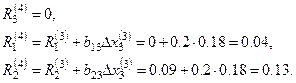
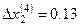 ,
,
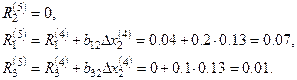
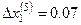 ,
,
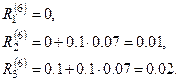
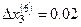 ,
,
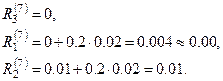
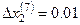 ,
,
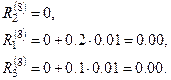
Окончательно получим: