Линейные уравнения и уравнения, приводимые к линейным
Учитель математики высшей категории
Цапиева Тамара Васильевна
Город Удомля Тверской области
Муниципальное общеобразовательное учреждение
«Удомельская средняя общеобразовательная школа № 5
С углубленным изучением отдельных предметов»
E-mail: eljvkz88@ mail.ru
Телефон: 89201618411
УРАВНЕНИЯ С ПАРАМЕТРОМ
(методическое пособие для учащихся 7-9 класс)
СОДЕРЖАНИЕ
· Пояснительная записка.
· .Уравнения с параметром, сводящие к линейным.
· .Квадратные уравнения с параметром.
· Применение теоремы Виета и исследование расположения
· корней квадратного уравнения относительно нуля.
· Расположения корней квадратной функции относительно
· заданных точек.
· Решение биквадратных уравнений с параметром.
· Уравнения с параметром, содержащие модуль.
Пояснительная записка.
Решение уравнений с параметрами можно считать деятельностью, близкой по своему характеру к исследовательской. Это обусловлено тем, что выбор метода решения, запись ответа предполагают определенный уровень сформированности умений наблюдать, сравнивать, анализировать, выдвигать и проверять гипотезу, обобщать полученные результаты.
Без сомнения, задачи с параметрами дают развивающий эффект, научный подход к решению задач. И в то же время наша программа не включает в себя этот важный раздел. С этим противоречием я и столкнулась, так как в наших школьных учебниках не содержится теоретического материала о решении заданий с параметрами, всего несколько упражнений, которые идут со звездочкой и не даются систематически. То есть, возникает противоречие между необходимостью увеличить объем информации, включаемый в общеобразовательную программу и возможностью ее усвоения каждым учеником.
Предложенное методическое пособие может быть использовано на уроках математики в 7 - 9 классах.
Решение уравнений с параметром.
В школе первые представления о параметре мы получаем при изучении прямой пропорциональности; линейной функции; линейного уравнения; уравнения первой степени; квадратного уравнения; исследования количества корней квадратного уравнения в зависимости от значений параметра.
Параметр, будучи фиксированным, но неизвестным числом, имеет как бы двойственную природу. Во-первых, предполагаемая известность позволяет «общаться» с параметром как с числом, а во-вторых,- степень свободы общения ограничивается его неизвестностью.
Обычно в уравнении буквами обозначают неизвестные. Решить уравнение– значит найти множество значений неизвестных, удовлетворяющих этому уравнению. Иногда уравнения кроме букв, обозначающих неизвестные, содержат другие буквы, называемые параметрами. Тогда мы имеем дело не с одним, а с бесконечным множеством уравнений. При этом бывает, что при одних значениях параметров уравнение не имеет корней, при других – имеет только один корень, при третьих – два корня. При решении таких уравнений надо сначала найти множество всех допустимых значений параметров, а затем разбить это множество на части, в каждой из которых ответ выражается одной и той же функцией через параметры.
.. Многие учащиеся слабо владеют методами их решения, часто воспринимают параметр как величину известную и проводят соответствующие выкладки без должного анализа различных ситуаций, диктуемых параметром. Отсюда неверные выводы, порою даже парадоксальные. Чтобы избежать этого, необходимо тщательно продумывать каждый шаг решения задачи с параметром, логически обосновывать любое преобразование, в котором участвует параметр.
Если в уравнении , кроме неизвестных, входят числа, обозначенные буквами, то они называются параметрами, а такое уравнение – параметрическим. Решить уравнение, содержащее параметр-это значит для каждого допустимого значения параметра найти множество всех значений данного уравнения.
Линейные уравнения и уравнения, приводимые к линейным.
Рассмотрим уравнение
 (1)
(1)
где 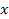 - неизвестная величина,
- неизвестная величина, 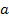 и
и  - параметры уравнения. Достаточно очевиден следующий результат.
- параметры уравнения. Достаточно очевиден следующий результат.
Теорема. Если  , то уравнение (1) при любом
, то уравнение (1) при любом 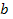 имеет единственное решение
имеет единственное решение  если
если 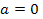 и
и  то уравнение (1) имеет бесчисленное множество решений (именно любое
то уравнение (1) имеет бесчисленное множество решений (именно любое 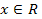 является решением уравнения (1); если
является решением уравнения (1); если 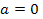 и
и 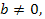 то уравнение (1) не имеет решений (т.е.
то уравнение (1) не имеет решений (т.е. 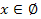 ).
).
1). Для каждого допустимого значения параметра 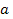 решить уравнение
решить уравнение
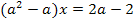
Решение. В данном уравнении допустимыми являются любые значения параметра 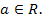 Уравнение равносильно такому уравнению:
Уравнение равносильно такому уравнению:
 (2)
(2)
Используя теорему 1, получаем
а) если 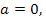 то уравнение (2) равносильно уравнению
то уравнение (2) равносильно уравнению
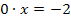 ⟺
⟺ 
б) если  то уравнение (3) равносильно уравнению
то уравнение (3) равносильно уравнению
 ⟺
⟺ 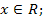
в) если 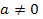 и
и 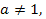 то из (3) следует, что
то из (3) следует, что 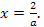
.
Ответ. Если 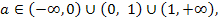 то
то 
если 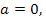 то
то 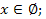 если
если  то
то 
2.) Решить уравнение : 
Решение. Если не учитывать теории линейных уравнений, то в лучшем случае можно получить ответ  , являющийся ошибочным, так как не учтены различные ситуации, связанные с параметром.
, являющийся ошибочным, так как не учтены различные ситуации, связанные с параметром.
Правильный же результат запишется так:
Если 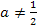 то
то 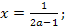 если
если 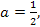 то
то 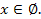
Ответ. Если 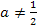 то
то 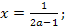 если
если 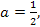 то
то 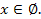
3).Решить уравнение: 
Решение. Если не принять во внимание, что в данном уравнении параметр 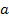 может принимать любые значения (в том числе и обращаться в нуль), то можно получит результат
может принимать любые значения (в том числе и обращаться в нуль), то можно получит результат  который является исчерпывающим лишь при
который является исчерпывающим лишь при  . Если же
. Если же 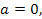 то уравнение приводится к виду
то уравнение приводится к виду 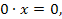 решением которого является любое число
решением которого является любое число 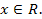
Ответ. Если 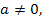 то
то  если
если  , то
, то 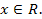
4).Решить и исследовать в зависимости от параметра уравнение:
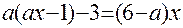
Решение:

 возможны три случая:
возможны три случая:
а) если 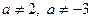 , т о уравнение имеет единственное решение
, т о уравнение имеет единственное решение
 ;
;
б) если  , то
, то  , а тогда решений нет;
, а тогда решений нет;
в)  то
то  и уравнение имеет бесконечное множество решений
и уравнение имеет бесконечное множество решений  .
.
Ответ: при 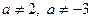

при  , решения нет;
, решения нет;
при 
 .
.
5). Для каждого допустимого значения параметра 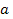 решить уравнение
решить уравнение
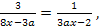
и указать все значения параметра, при которых корни уравнения больше 
Решение. В данном уравнении допустимыми являются любые значения параметра 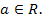 При каждом значении параметра уравнение равносильно системе
При каждом значении параметра уравнение равносильно системе



⟺ (3)


Решим сначала уравнении системы (3); оно линейно и по теореме 1 имеем:
а) если 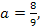 то указанное уравнение равносильно такому уравнению:
то указанное уравнение равносильно такому уравнению:
 ⟺
⟺ 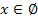 ;
;
б) если 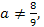 то
то 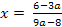 .
.
Найдем теперь те значения параметра 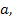 при которых найденное решение уравнения удовлетворяет неравенствам из (3).
при которых найденное решение уравнения удовлетворяет неравенствам из (3).
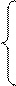 |
 8∙
8∙ 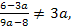
⟺ ⟺  ⟺
⟺ 
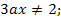

Итак, если 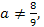
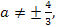 то данное уравнение имеет единственный корень
то данное уравнение имеет единственный корень
 если же
если же  или
или  то данное уравнение корней не имеет .
то данное уравнение корней не имеет .

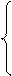
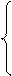 Найдем теперь те значения параметра
Найдем теперь те значения параметра 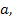 при которых найденный корень превосходит
при которых найденный корень превосходит  . Имеем
. Имеем
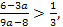


⟺ ⟺
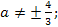
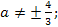
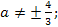
⟺ 

Ответ. Если 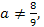
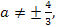 то
то 
если  или
или 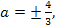 то
то 
Если  то корень больше
то корень больше 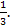
6).Решить уравнение. 
Решение.
Обозначим 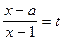 , где
, где  получим уравнение
получим уравнение
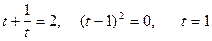
Подставим  , получим
, получим 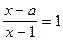 ,
,
Откуда 
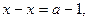 то есть
то есть
 .
.
Возможны два случая:
а) если 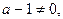 т.е.
т.е.  , то решения нет;
, то решения нет;
в) если 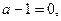 т.е.
т.е. 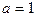 , то
, то  ,
,
значит последнее уравнение имеет бесконечное множество решений  .
.
Однако надо проверить, что  следовательно, исходное уравнение имеет решение
следовательно, исходное уравнение имеет решение  .
.
Ответ: при 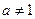 , решений нет
, решений нет
при 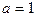 , то
, то 
7).Решить уравнение. 
Решение:
Уравнение равносильно системе:
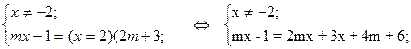
Последнее уравнение перепишем в виде  ;
;

При  получаем
получаем  нет корней.
нет корней.
При 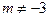 получаем
получаем 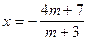 единственное решение.
единственное решение.
Однако надо проверить, что 

Ответ: при 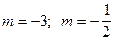 нет решения;
нет решения;
при 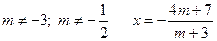 .
.
8).Решить уравнение.  ОДЗ:
ОДЗ: 
Решение:
Упростим уравнение.
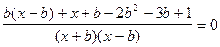 ,
,
 ,
,
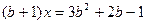 ,
,
 ,
,
Последнее уравнение является линейным относительно х, и оно равносильно исходному в ОДЗ заданного уравнения.
1) При  уравнение имеет единственное решение
уравнение имеет единственное решение
 .
.
Полученное решение входит в ОДЗ, если
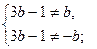

Таким образом исходное уравнение имеет единственное решение
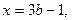 при
при 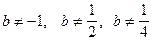 .
.
2) при 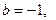 линейное уравнение примет вид
линейное уравнение примет вид  и, значит, имеет бесконечное множество решений
и, значит, имеет бесконечное множество решений  ,
, 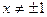
3) при  уравнение очевидно решений не имеет.
уравнение очевидно решений не имеет.
Ответ: при 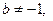

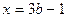
при 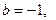
 ,
, 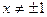
при  решений нет.
решений нет.
9).При каком значении а уравнение имеет единственное решение
 ОДЗ
ОДЗ 
Решение:
Упростим уравнение:

Последнее уравнение является линейным относительно х , и оно равносильно исходному в ОДЗ заданного уравнения.
При 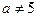 уравнение имеет единственное решение
уравнение имеет единственное решение

Полученное решение входит в ОДЗ, если
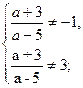 ОДЗ
ОДЗ 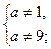
Ответ: при 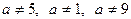
Задачи для самостоятельного решения:
1). Найти значения параметра m , при которых уравнение
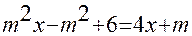
а) имеет единственное решение,
б) не имеет решений,
в) имеет бесконечное множество решений.
Ответ:
a) 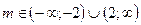
б) 
в)  .
.
2) При каких значениях параметра а уравнение

имеет единственное решение
Ответ 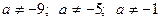 .
.
3). При каких значениях параметра а уравнение

имеет единственное решение
Ответ 
4). При каких значениях параметра а уравнение
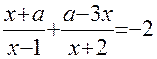
имеет единственное решение
Ответ: 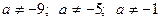 .
.
