Свойства бесконечно малых функций
Предел функции.
1. Предел функции в точке.
Односторонние пределы.
Пример.
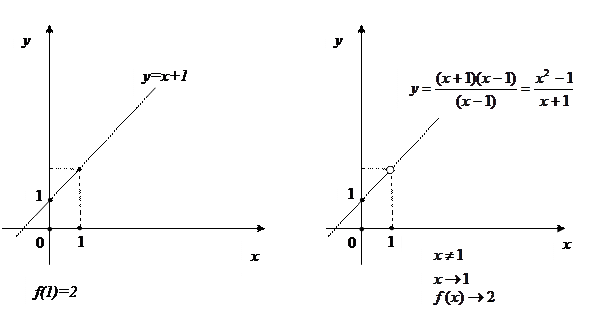
Пусть функция y=f(x) задана в некоторой окрестности точки 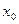 , за исключением, быть может, самой точки
, за исключением, быть может, самой точки 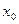 .
.
Опр. 1. Точка А называется пределом функции y=f(x) при 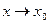 , если для любой последовательности точек
, если для любой последовательности точек 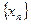 , сходящейся к
, сходящейся к 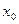 , последовательность значений функции
, последовательность значений функции 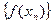 сходится к А. В этом случае пишут:
сходится к А. В этом случае пишут: 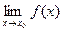 =А, или
=А, или 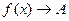 при
при  .
.
Это определение называют определением предела по Гейне (нем. математик XIX в.)
Замечание. Если точка 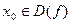 , то предел
, то предел 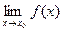 , если он существует, равен значению функции в данной точке
, если он существует, равен значению функции в данной точке 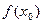 . (См. рис.1)
. (См. рис.1)
Опр. 2. Если при стремлении к 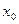 x принимает лишь значения, меньшие (большие)
x принимает лишь значения, меньшие (большие) 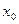 , и при этом
, и при этом 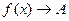 , то говорят об одностороннем пределе слева
, то говорят об одностороннем пределе слева 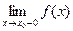 (справа
(справа 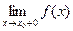 ).
).
Пример. 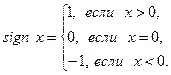
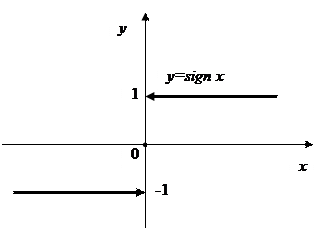
Утверждение. Предел функции в точке существует тогда и только тогда, когда существуют и равны оба односторонних предела функции в данной точке.
Существует и другое (равносильное) определение предела функции, в котором используется понятие окрестности. Оно называется определением по Коши.
Опр. 3. Число А называется пределом функции y=f(x) при 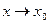 , если для любого, даже сколь угодно малого положительного числа
, если для любого, даже сколь угодно малого положительного числа 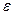 , найдется такое положительное число
, найдется такое положительное число 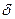 , зависящее от
, зависящее от 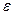 , что для всех x, удовлетворяющих условию
, что для всех x, удовлетворяющих условию 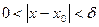 , верно неравенство
, верно неравенство 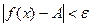 .
.
В символической форме это определение записывается так:
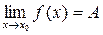
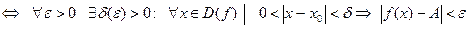 .
.
Вопрос. Где здесь окрестности? Раскрыть скобки в неравенствах.
Опр.3 можно также сформулировать в следующем общем виде:
Число А называют пределом функции y=f(x) при 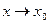 и пишут
и пишут 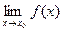 =А, если
=А, если 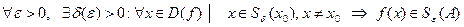 .
.
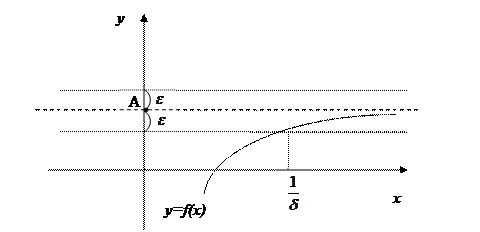
Геометрический смысл данного определения 3 заключается в следующем: какую бы (даже сколь угодно малую) окрестность точки А на оси Оу мы ни взяли, всегда найдется окрестность точки 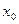 на оси Ох, являющаяся ее прообразом.
на оси Ох, являющаяся ее прообразом.
2. Бесконечные пределы.
Общее определение предела позволяет дать определение и для случаев, когда 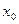 или А являются несобственными точками, т.е.
или А являются несобственными точками, т.е. 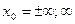 .
.
Опр. 4. Число А называют пределом функции y=f(x) при 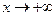 и пишут
и пишут 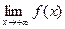 =А, если:
=А, если:
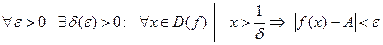 .
.
Опр. 5. Число А называют пределом функции y=f(x) при 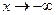 и пишут
и пишут 
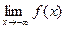 =А, если:
=А, если:
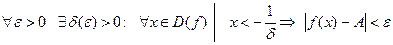 .
.
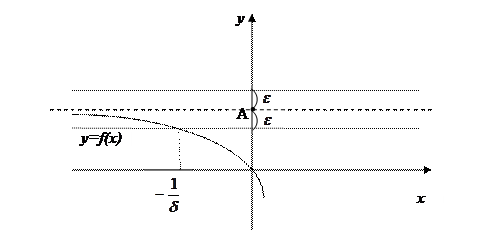

Самостоятельно: сформулировать определение предела при 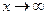 .
.
Опр.6. Говорят, что функция y=f(x) имеет предел при  , равный
, равный 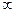 и пишут
и пишут 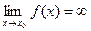 , если:
, если:
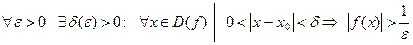 .
.

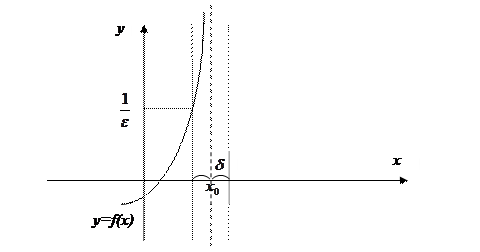
Самостоятельно: сформулировать определение предела, равного 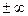 .
.
3. Бесконечно малые и бесконечно большие функции, их связь.
Опр. Функция 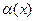 называется бесконечно малой при
называется бесконечно малой при  функцией, если ее предел при
функцией, если ее предел при  равен нулю:
равен нулю:
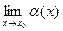 =0
=0 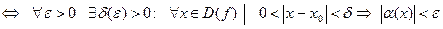 .
.
Опр. Функция 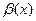 называется бесконечно большой при
называется бесконечно большой при  функцией, если ее предел при
функцией, если ее предел при  есть несобственное число:
есть несобственное число:
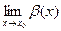 =
= 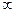
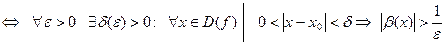 .
.
Пример. Функция 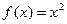 является: БМ при
является: БМ при 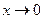 ; ББ при
; ББ при 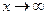 ; не является ни БМ, ни ББ при
; не является ни БМ, ни ББ при 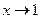 .
.
Теорема 1. (о связи предела и бесконечно малой функции). Если функция
y=f(x) имеет предел 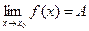 , то разность между функцией и значением ее предела есть бесконечно малая при
, то разность между функцией и значением ее предела есть бесконечно малая при  .
.
Док-во. Имеем:
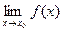 =А
=А 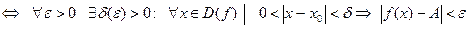 .
.
Надо доказать, что 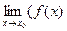 -А)=0, т.е.
-А)=0, т.е.
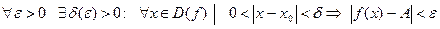 . Очевидно, что это условие выполнено. ▲
. Очевидно, что это условие выполнено. ▲
Следствие. Если функция y=f(x) имеет предел 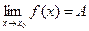 , то ее можно представить в виде суммы этого числа А и бесконечно малой при
, то ее можно представить в виде суммы этого числа А и бесконечно малой при  функции
функции 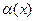 :
: 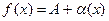 .
.
Теорема 2 ( о связи БМ и ББ функций). Если 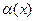 есть БМ
есть БМ  Ф, и
Ф, и 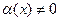 в некоторой окрестности точки
в некоторой окрестности точки 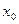 , то функция
, то функция 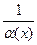 есть ББ
есть ББ  Ф. Если
Ф. Если 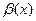 есть ББ
есть ББ  Ф, то функция
Ф, то функция 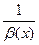 есть БМ
есть БМ  Ф.
Ф.
Доказать самостоятельно, используя определение предела.
4. Свойства бесконечно больших и бесконечно малых функций.
Свойства бесконечно малых функций.
1. Алгебраическая сумма конечного числа БМ  Ф есть БМФ при
Ф есть БМФ при  .
.
2. Произведение БМ  Ф на ограниченную в некоторой окрестности точки
Ф на ограниченную в некоторой окрестности точки 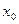 функцию (в т.ч. на постоянную, на другую БМ) есть БМ
функцию (в т.ч. на постоянную, на другую БМ) есть БМ  Ф.
Ф.
3. Частное от деления БМ  Ф на функцию, предел которой отличен от нуля, есть БМ
Ф на функцию, предел которой отличен от нуля, есть БМ  Ф.
Ф.
Замечание. Свойство 3 не рассматривает предел отношения двух БМ  Ф из-за его неопределенности: он может быть равен как конечному числу, так и
Ф из-за его неопределенности: он может быть равен как конечному числу, так и 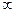 .
.
Докажем, например, свойство 1.
Пусть 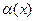 и
и 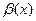 есть БМ
есть БМ  Ф. Докажем, что функция
Ф. Докажем, что функция 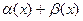 также есть БМ
также есть БМ  Ф.
Ф.
По условию для любого 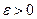 , а значит, и для
, а значит, и для 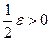 найдутся такие числа
найдутся такие числа 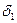 и
и 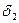 , что
, что 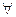
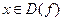 :
:
если 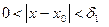 , то
, то
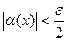 (1)
(1)
если 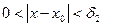 , то
, то
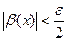 (2)
(2)
Если в качестве 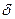 взять минимальное из
взять минимальное из 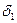 и
и 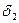 , т.е.
, т.е. 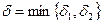 , то для всех х, удовлетворяющих условию
, то для всех х, удовлетворяющих условию 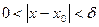 будут верны оба неравенства (1) и (2). Складывая их почленно, получим:
будут верны оба неравенства (1) и (2). Складывая их почленно, получим:
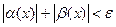 .
.
Используя первое неравенство треугольника, перейдем к более сильному неравенству:
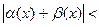
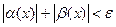 .
.
Итак, 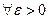 мы нашли
мы нашли 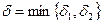 , такое, что при всех
, такое, что при всех 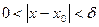 выполняется неравенство
выполняется неравенство 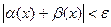 . Это и означает, что функция
. Это и означает, что функция 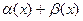 есть БМ
есть БМ  Ф. ▲
Ф. ▲
Свойства бесконечно больших функций.
1. Произведение ББ  Ф на функцию, предел которой отличен от 0, есть ББ
Ф на функцию, предел которой отличен от 0, есть ББ  Ф.
Ф.
2. Сумма ББ  Ф и ограниченной функции есть ББ
Ф и ограниченной функции есть ББ  Ф.
Ф.
3. Сумма ББ  Ф одного знака есть ББ
Ф одного знака есть ББ  Ф того же знака.
Ф того же знака.
4. Частное от деления ББ  Ф на функцию, имеющую конечный предел, есть ББ
Ф на функцию, имеющую конечный предел, есть ББ  Ф.
Ф.
Сравнение бесконечно малых функций.
Пусть 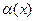 и
и 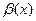 - БМ
- БМ  Ф. Предположим, что существует предел их отношения, равный некоторому значению А (собств. или несобств.), т.е.
Ф. Предположим, что существует предел их отношения, равный некоторому значению А (собств. или несобств.), т.е.
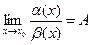 . Тогда если:
. Тогда если:
1) А – число, не равное 0 или 1, то функции 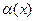 и
и 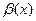 называются БМ одинакового порядка.
называются БМ одинакового порядка.
2) А=0, то функция 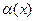 называется БМ более высокого порядка малости, чем
называется БМ более высокого порядка малости, чем 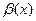 и обозначают:
и обозначают: 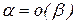 (о малое).
(о малое).
Пример:
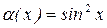 ,
, 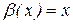 - БМ при х→0,
- БМ при х→0,
3) А= 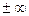 , то функция
, то функция 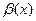 называется БМ более высокого порядка малости, чем
называется БМ более высокого порядка малости, чем 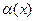 .
.
4) А =1, то функции 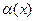 и
и 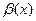 называются эквивалентными БМ
называются эквивалентными БМ  , обозначается:
, обозначается: 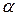 ~
~ 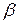 .
.
