Схема нахождения наибольшего и наименьшего значений функции
1. Найти О.О.Ф.
2. Найти 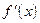 в О.О.Ф.
в О.О.Ф.
3. Найти критические точки в О.О.Ф.:
4. а).в которых выполняется равенство 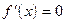 ;
;
5. б) в которых 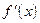 не существует.
не существует.
6. Изобразить на числовой оси О.О.Ф. и все ее критические точки.
7. Определить интервалы знакопостоянства производной в каждом из промежутков на которые критические точки разбивают О.О.Ф.
8. На основании достаточных условий экстремума сделать заключение о экстремуме функции в каждой из указанных в п.3 критических точках.
9. Найти значения функции в критических точках внутри промежутка и на концах промежутка (если это числа).
10. Из всех найденных значений в п.7 выбрать наибольшее и наименьшее значения.
Пример 21. Найти наибольшее и наименьшее значения функции 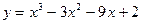 на отрезке [-2; 2].
на отрезке [-2; 2].
Решение. О.О.Ф.: х Î R;
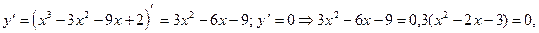
х1 = -1, х2 = 3 – критические точки; x1 = -1 Î [-2; 2], x2 = 3 Ï [-2; 2].
х1 = -1 – единственная критическая точка на [-2; 2].

у(-1)=(-1)3-3(-1)2-9(-1)+2=-1-3+9+2=7 (наибольшее);
у(2)= (2)3-3(2)2-9×(2)+2=8-12-18+2=-20 (наименьшее);
у(-2)= (-2)3-3×(-2)2-9×(-2)+2=-8-12+18+2=0. Ответ: 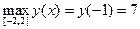
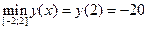
Пример 22. Найти наибольшее и наименьшее значения функции 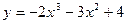 на промежутке [1; 3).
на промежутке [1; 3).
Решение. О.О.Ф.: x Î R;
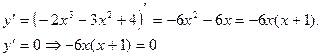
х1 = 0, х2 =-1 – критические точки.

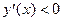 на [1; 3).
на [1; 3).
На промежутке [1; 3) данная функция убывает:
у(1) = -2×(1)3 -×3(1)2 + 4 = -2-3+4 = -1.
Наибольшее значение функция достигает на левом конце промежутка:
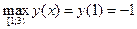 .
.
Наименьшее значение в промежутке [1; 3) функция не достигает, так как точка х =3 не принадлежит этому промежутку.
Ответ: 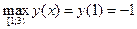
Пример 23. Требуется огородить проволочной сеткой длины 32 м прямоугольный участок, прилегающий к стене. Найти размеры участка, при которых его площадь будет наибольшей.
 |
Решение. Обозначим стороны прямоугольника через АВ = СD = x, BC = AD = y. Тогда его площадь S = xy.
Так как 2х + у = 32, получим 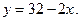 Тогда
Тогда 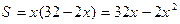 . Найдем О.О.Ф. площади:
. Найдем О.О.Ф. площади:
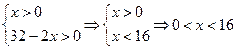 .
.
Найдем наибольшее значение функции S на интервале (0; 16).
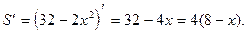
х = 8 – единственная критическая точка.

х = 8 – единственная точка максимума, значит
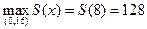 .
.
Размеры участка: ширина – х = 8; длина – у = 32-16=16.
Ответ: 8 м и 16 м.
Задачи раздела I.
1. Найти производную функции в точке x0:
1) 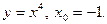
2) 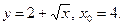
3) 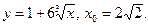
4) 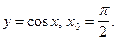
5) 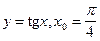
6) 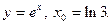
7) 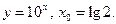
8) 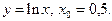
9) 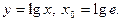
2. Найти производную функции, предварительно приведя ее к виду kxm(mÎZ).
1) 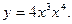 3)
3) 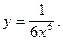
2) 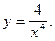 4)
4) 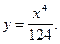
3. Приведя функцию к к виду kxa(aÎQ) найти ее производную.
1) 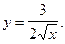
2) 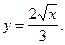
3) 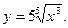
4) 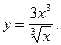
5) 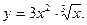
4. Используя формулу производной от суммы найти производную функции:
1) 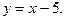
2) 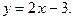
3) 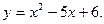
4) 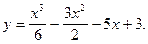
5) 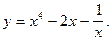
6) 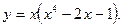
7) 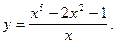
5. Используя формулы производной произведения или частного, найти производную функции:
1) 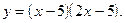
2) 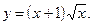
3) 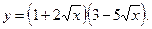
4) 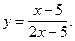
5) 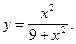
6) 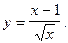
6.Используя правило дифференцирования сложной функции, найти производную функции:
1) 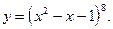
2) 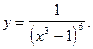
3) 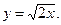
4) 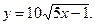
5) 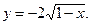
6) 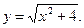
7) 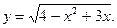
7. Найти критические точки функции:
1) 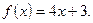
2) 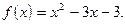
3) 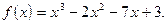
4) 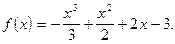
5) 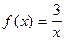
6) 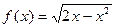
8. Найти промежутки возрастания и убывания функции:
1) 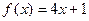
2) 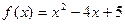
3) 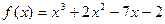
4) 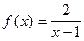
5) 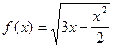
9. Найти точки экстремума и экстремумы функции.
1) 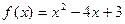
2) 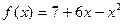
3) 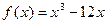
4) 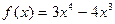
5) 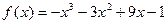
6) 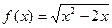
10. Найти наибольшее и наименьшее значения функции на промежутке.
1) 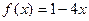 на [-3; 2]
на [-3; 2]
2) 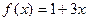 на [-2; 3)
на [-2; 3)
3) 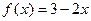 на (-1; 2]
на (-1; 2]
4) 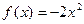 на [-2; 1]
на [-2; 1]
5) 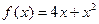 на [-1; 0]
на [-1; 0]
6) 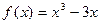 на [0; 3]
на [0; 3]
11. Периметр прямоугольника равен 40. Найти его стороны, при которых его площадь будет наибольшей.
Задачи раздела II.
1. Найти производную функции в точке x0:
1) 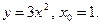
2) 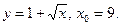
3) 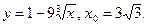
4) 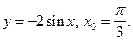
5) 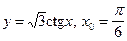
6) 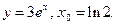
7) 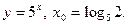
8) 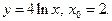
9) 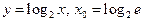
2. Найти производную функции, предварительно приведя ее к виду kxm(mÎZ).
1) 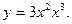
2) 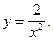
3) 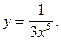
4) 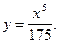
3. Приведя функцию к к виду kxa(aÎQ) найти ее производную.
1) 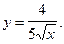
2) 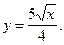
3) 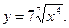
4) 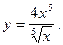
5) 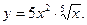
4. Используя формулу производной от суммы найти производную функции:
1) 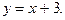
2) 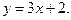
3) 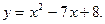
4) 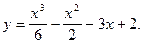
5) 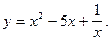
6) 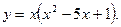
7) 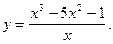
5. Используя формулы производной произведения или частного, найти производную функции:
1) 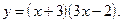
2) 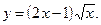
3) 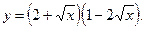
4) 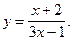
5) 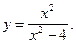
6) 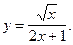
6.Используя правило дифференцирования сложной функции, найти производную функции:
1) 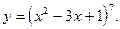
2) 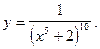
3) 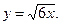
4) 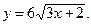
5) 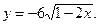
6) 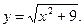
7) 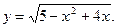
7. Найти критические точки функции:
1) 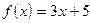
2) 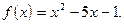
3) 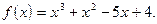
4) 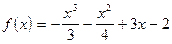
5) 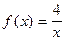
6) 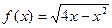
8. Найти промежутки возрастания и убывания функции:
1) 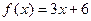
2) 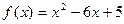
3) 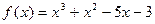
4) 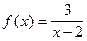
5) 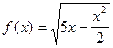
9. Найти точки экстремума и экстремумы функции.
1) 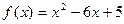
2) 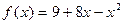
3) 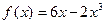
4) 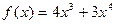
5) 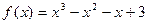
6) 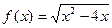
10. Найти наибольшее и наименьшее значения функции на промежутке.
1) 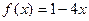 на [-3; 2]
на [-3; 2]
2) 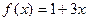 на [-2; 3)
на [-2; 3)
3) 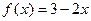 на (-1; 2]
на (-1; 2]
4) 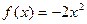 на [-2; 1]
на [-2; 1]
5) 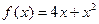 на [-1; 0]
на [-1; 0]
6) 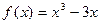 на [0; 3]
на [0; 3]
