Полиномы Чебышева. Представление функции полиномом Чебышева

Во-первых, полиномы Чебышева обладают таким важным свойством: если на нелинейный элемент, статическая характеристика которого представляет собой полином Чебышева некоторой степени n, подать гармонический сигнал, например, косинусоидальный (синусоидальный), единичной амплитуды, то на выходе такого нелинейного элемента также будет гармонический сигнал единичной амплитуды, но с n-кратной частотой.

Во-вторых, полиномы Чебышева растут за пределами интервала [-1, 1] наиболее быстро из всех полиномов такой же степени. Их используют для синтеза линейных фильтров [2]. И такие фильтры при заданной неравномерности в полосе пропускания обладают наиболее крутой частотной характеристикой в полосе запирания по сравнению с другими фильтрами того же порядка.

В-третьих, полиномы Чебышева являются набором ортогональных с весом функций [1], что позволяет представить, например, однозначную статическую характеристику нелинейного безинерционного звена в виде довольно быстро сходящегося ряда.

Полиномы Чебышева имеют вид[1, 2]:

(1)

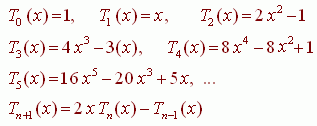
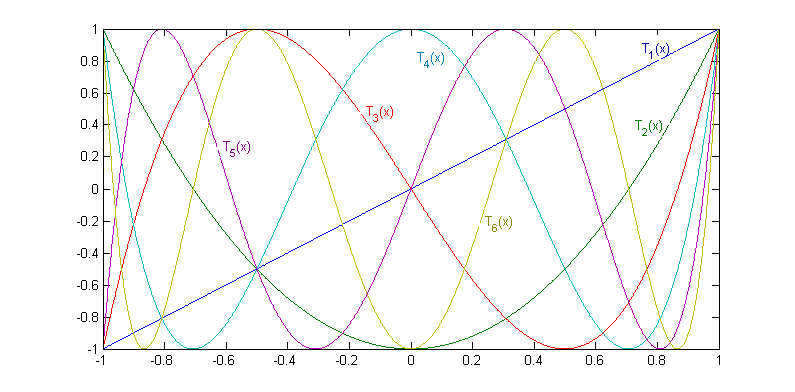
Графики первых пяти полиномов Чебышева представлены на рисунке:

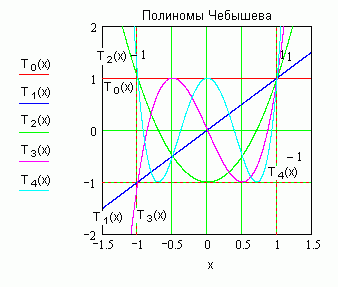
Рис. 1.1. Полиномы Чебышева. Полином Чебышева на интервале (-1, 1) ограничен значениями (-1, 1), а за пределами этого интервала растет по абсолютной величине быстрее любого другого полинома той же степени, ограниченного тем же условием

Если вы впервые увидели полиномы Чебышева, то обратим внимание и на такое их представление:

(2)

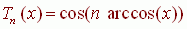
что на первый взгляд непостижимым образом, но очень красиво связывает тригонометрию и алгебру.

Полиномы Чебышева

Полиномы Чебышева первого рода представляют собой ортогональную систему функций и определяются следующим образом:

.

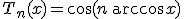Например,

,

,

,

,

,

.

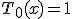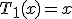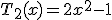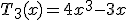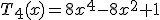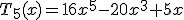Используя тригономитрические соотношения для косинусов суммы и разности, можно вывести рекуррентное соотношение для нахождения полиномов Чебышева:

.

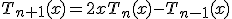Полином T_n(x) имеет на отрезке [-1,1] ровно n корней, расположенных в точках

.

Любую функцию f(x), определённую на отрезке [-1,1] можно приблизить следующей формулой:

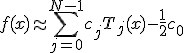, где

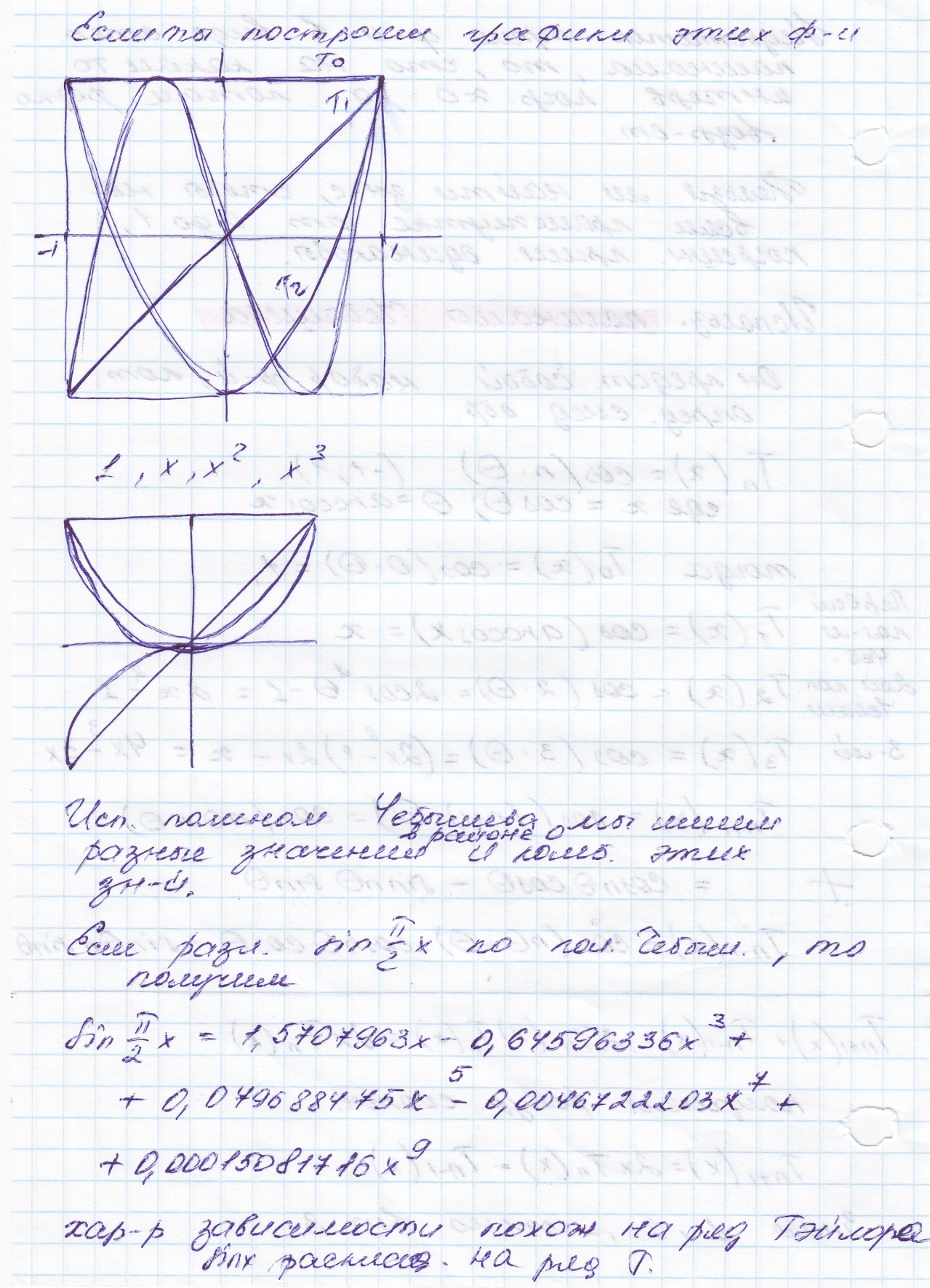
Представление функции рациональной и непрерывной дробью

Метод экономизации

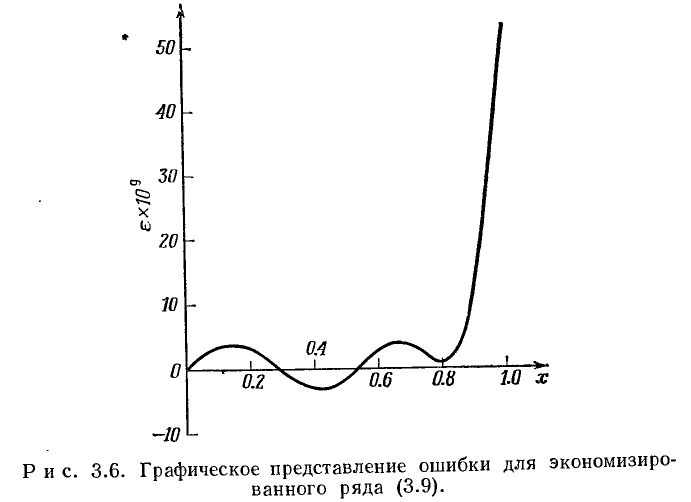
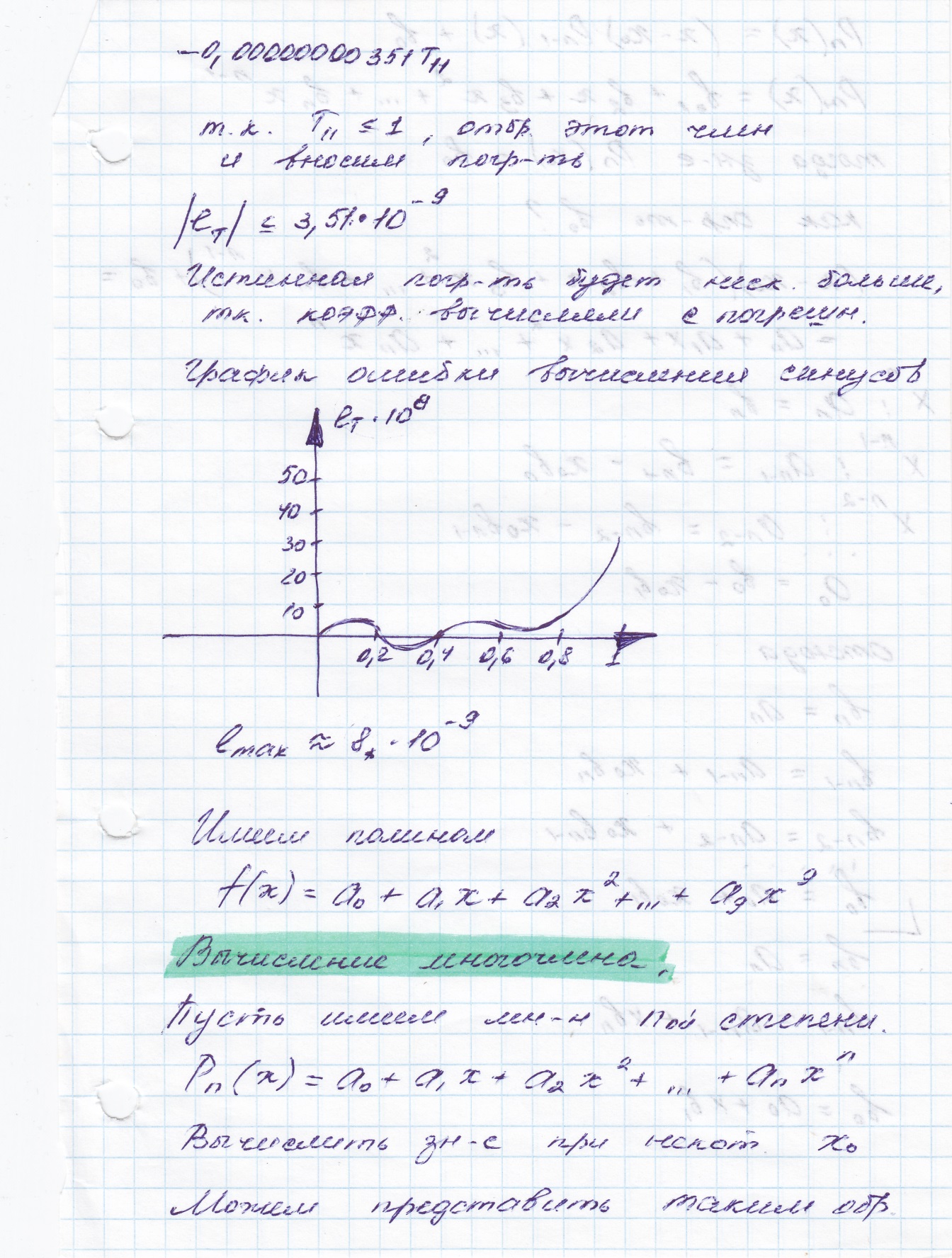
Схема Горнера вычисления полинома

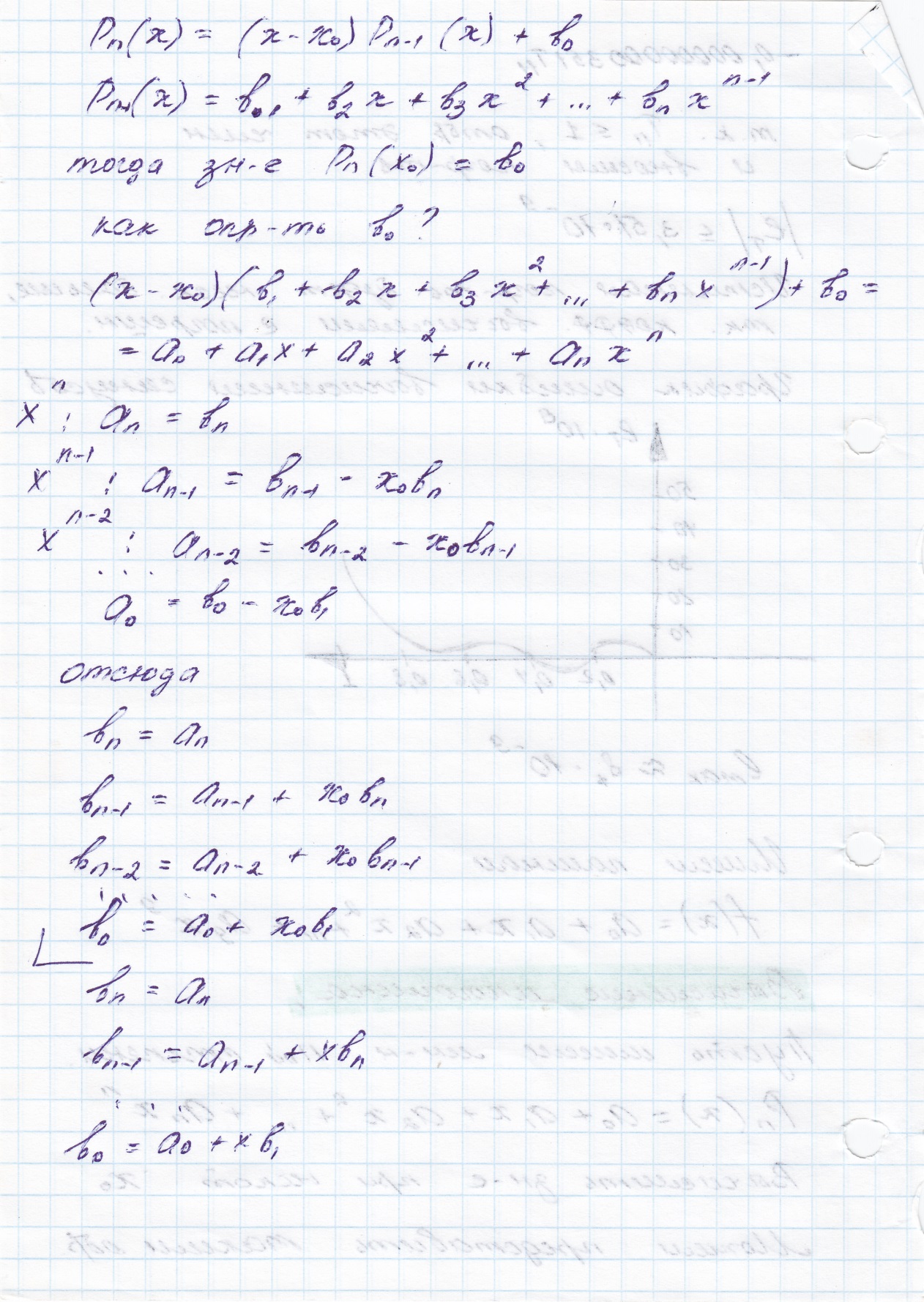
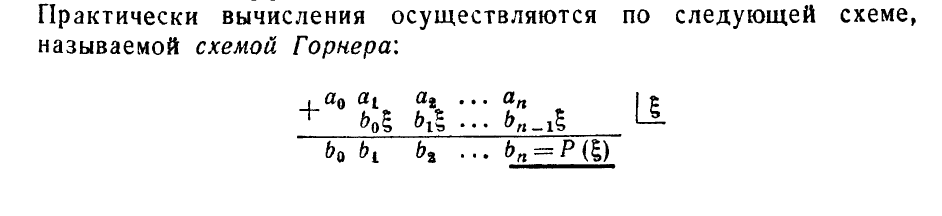
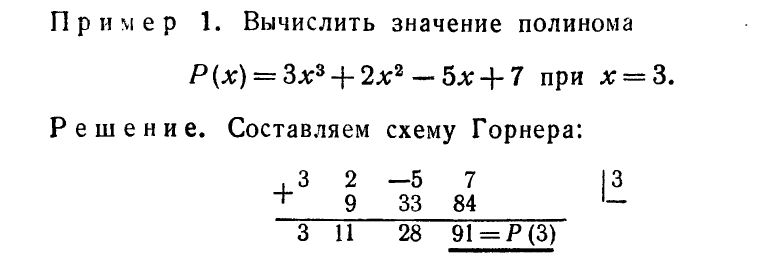
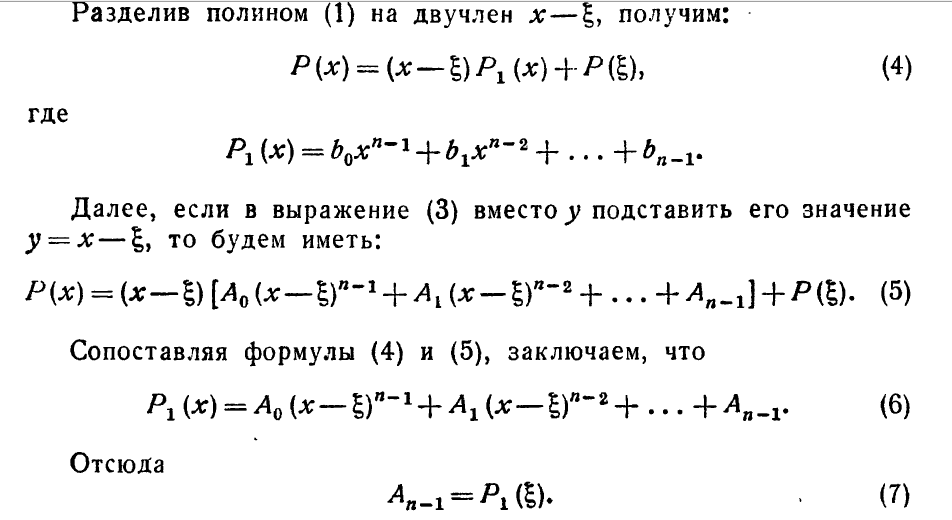
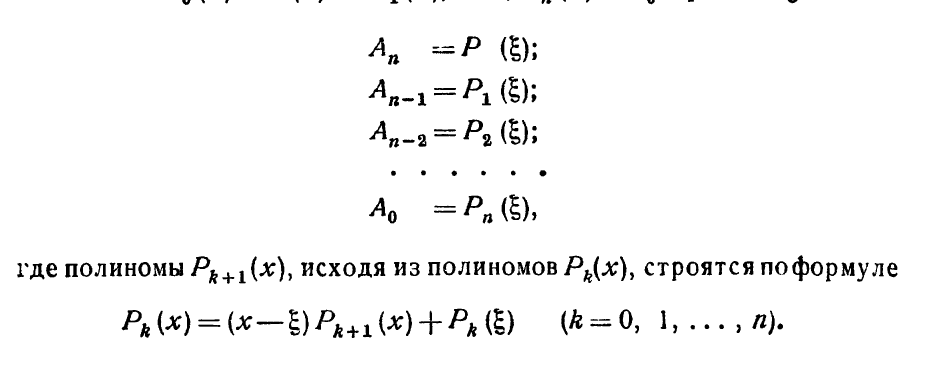
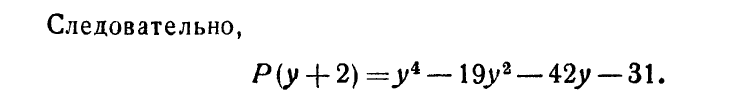
Границы всех корней полинома

Границы действительных корней полинома

Методы уточнения действительных корней нелинейного уравнения (половинного и пропорционального деления, Ньютона, комбинированный, итерационный, усов.итетерации). условие сходимости итерационных методов.

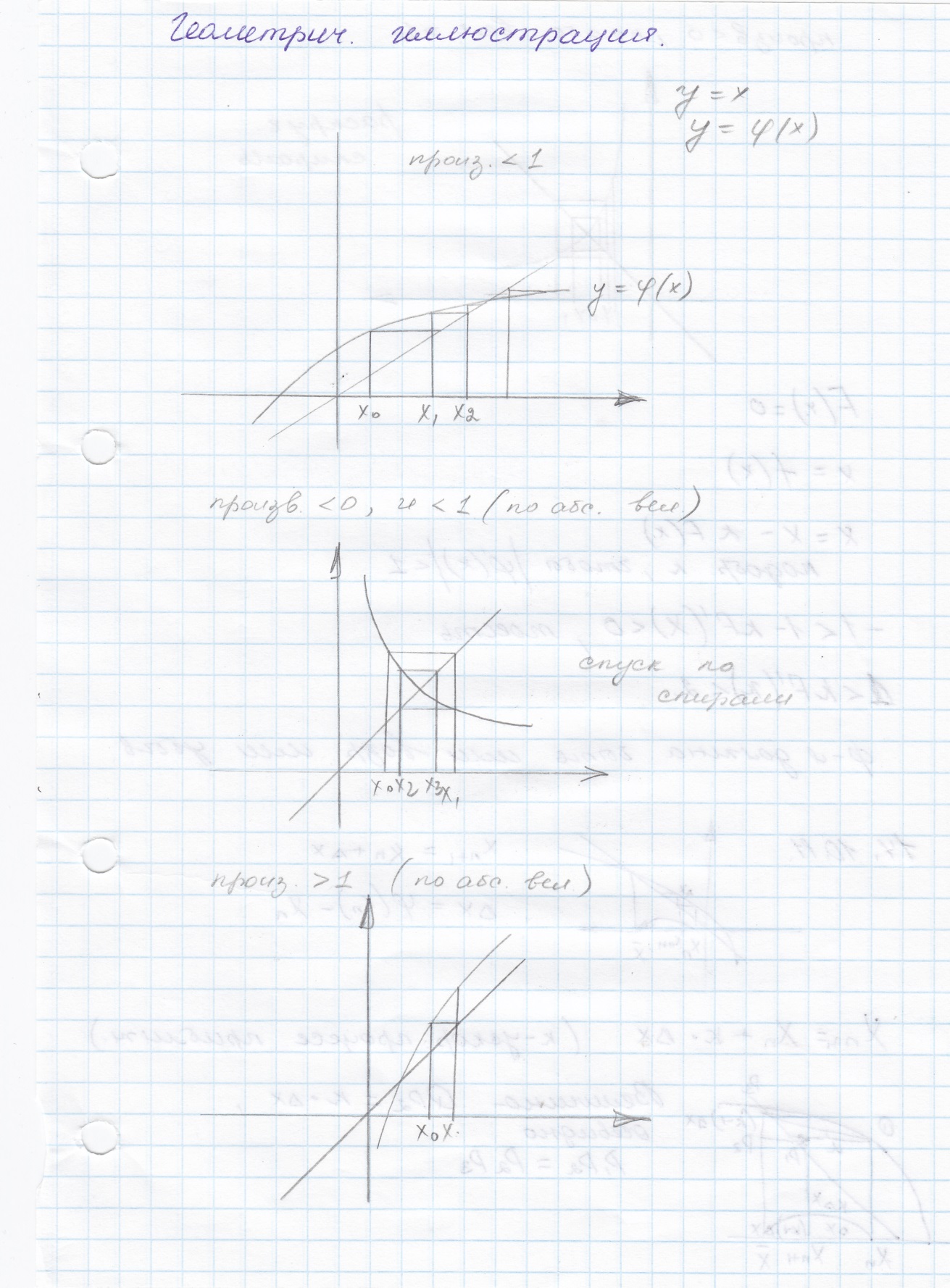
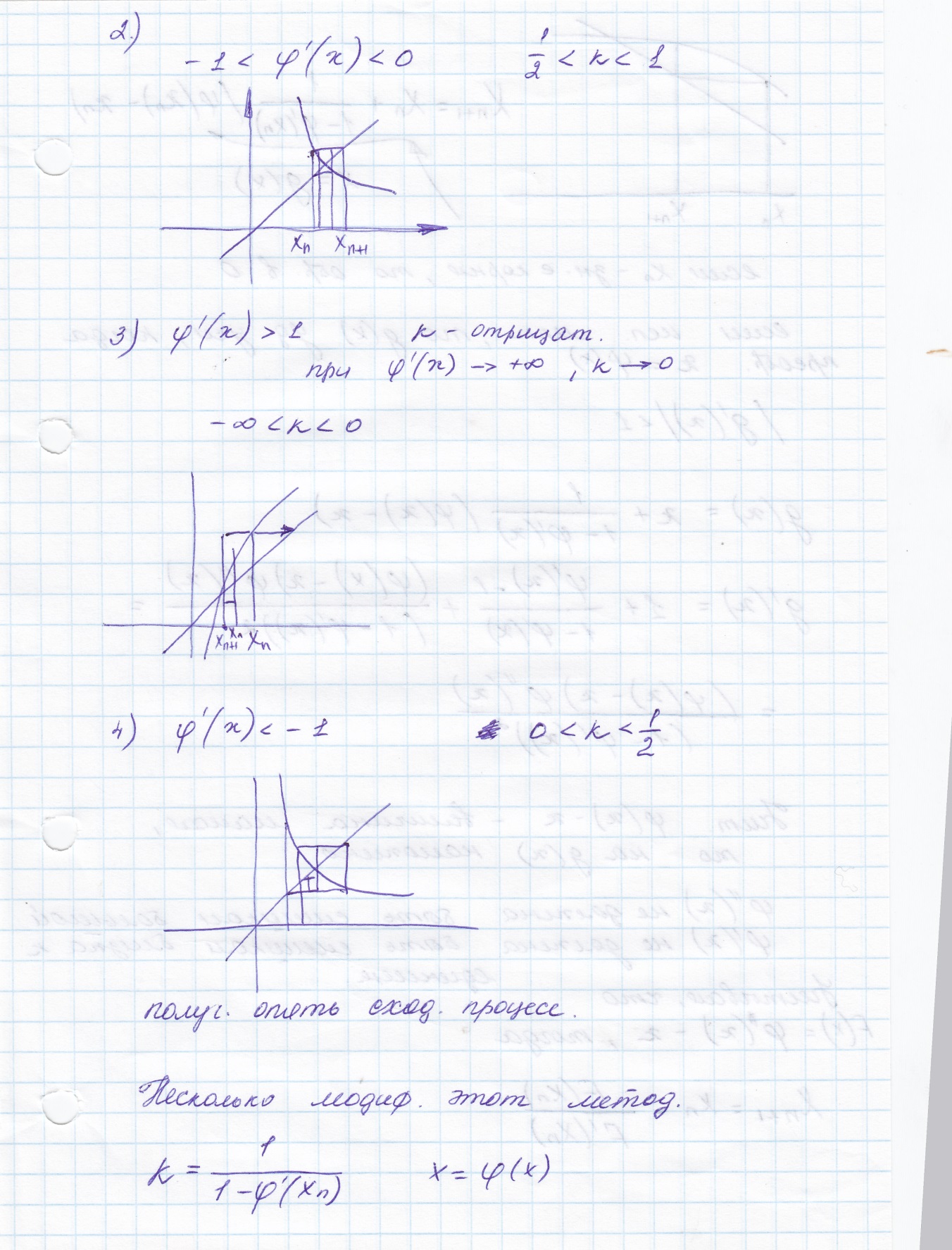
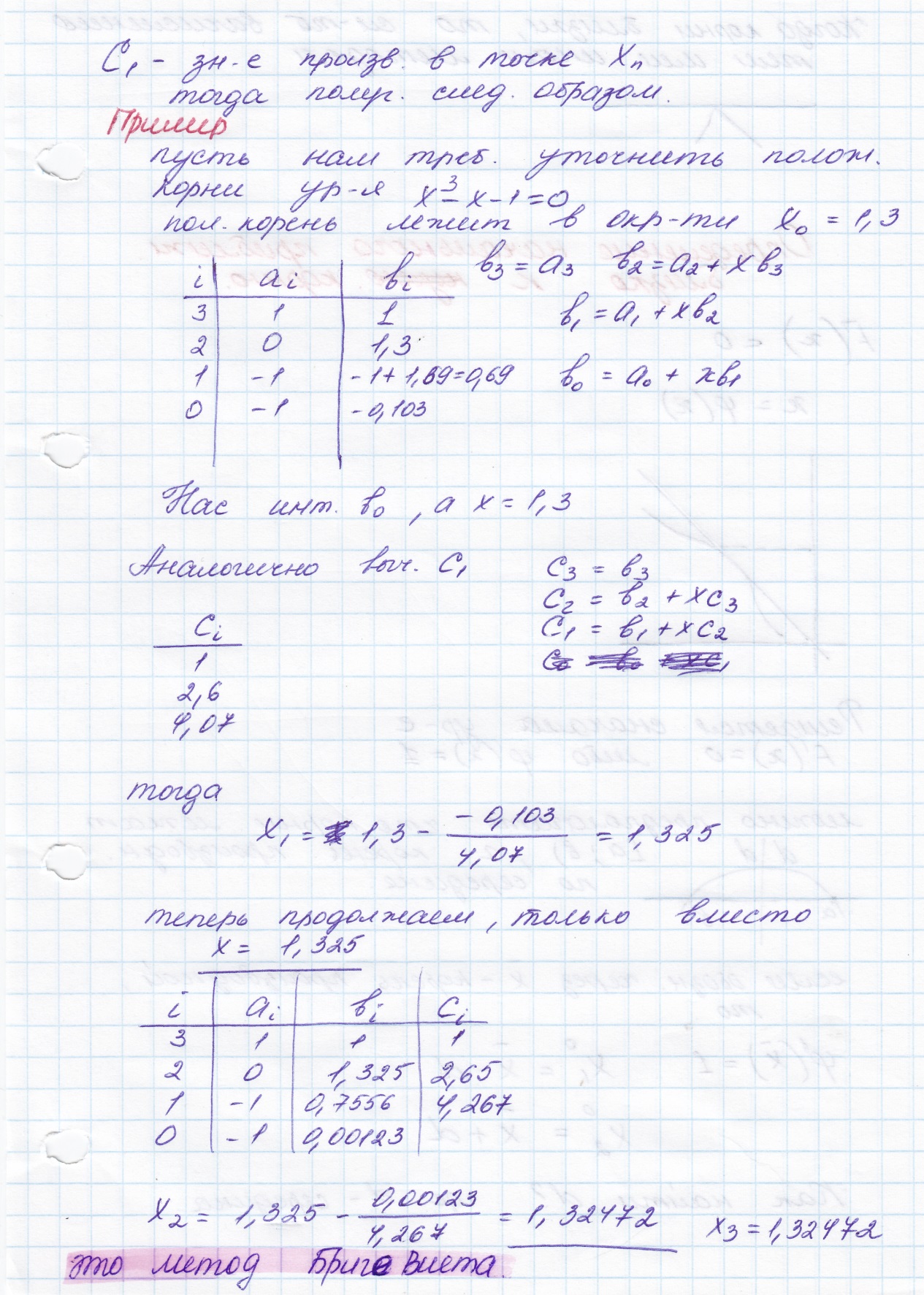
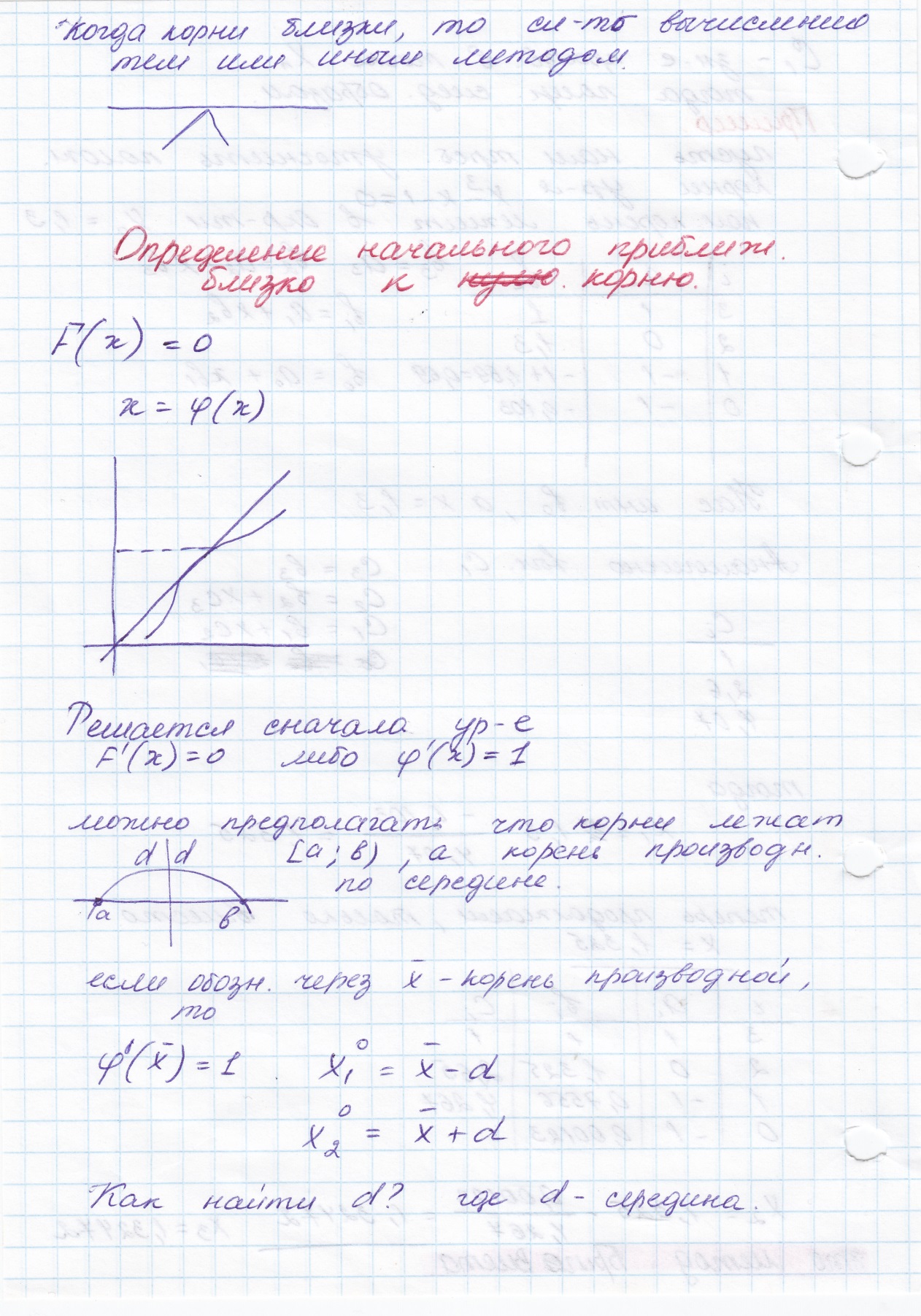
Нахождение начальных значений близких нулей многочлена

15. Метод Бриге-Виетта = 13