Уравнение Бернулли для реальной жидкости

ИНСТИТУТ ЭНЕРГЕТИКИ И АВТОМАТИКИ

Кафедра теплотехнических

и энергетических систем

ПОСТРОЕНИЕ ЛИНИИ ПЬЕЗОМЕТРИЧЕСКОГО ДАВЛЕНИЯ

Методические указания по выполнению

лабораторной работы для студентов всех

специальностей, изучающих теплотехнические

дисциплины

Магнитогорск

Составители: Ю. И. Тартаковский

Т.П. Семенова

Построение линии пьезометрического давления. Методические указания по выполнению лабораторной работы для студентов всех специальностей, изучающих теплотехнические дисциплины . Маг­нитогорск: ГОУ ВПО «МГТУ», 2012. 10 с.

Рецензент

©Ю. И. Тартаковский,

Т.П.Семенова, 2012

ПОСТРОЕНИЕ ЛИНИИ ПЬЕЗОМЕТРИЧЕСКОГО ДАВЛЕНИЯ

ЦЕЛЬ РАБОТЫ

Подтверждение экспериментальным путем построения линии пьезометрического давления уравнения Бернулли.

ИСПОЛЬЗУЕМОЕ ОБОРУДОВАНИЕ

Стационарный гидравлический стенд, пьезометры и трубки Пито.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Для изучения режима давления в тепловых сетях и местных системах зданий широко используются пьезометрические графики. На пьезометрическом графике в определенном масштабе наносят рельеф местности. Вдоль тепловых трасс, указывают высоты присоединенных зданий, показывают напор в подающей и обратных линиях теплопроводов. Роль пьезометрических графиков при разработке гидравлических режимов систем теплоснабжения очень велика, так как он позволяет наглядно показать допустимые границы давлений во всех элементах системы. В населенных пунктах тепловые сети заглубляют примерно на один метр, при вычерчивании профиля теплопровода его ось условно совмещают с поверхностью земли. За горизонтальную плоскость отчета принимается плоскость сравнения О-О , показанная на рис.1. Величина 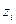показывает геодезическую высоту оси трубопровода в точке 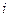над плоскостью отсчета.

Рассмотрим трубопровод переменного диаметра, расположенный в пространстве под углом (рис1).

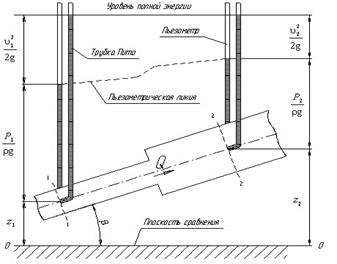
Рис 1. Схема к выводу уравнения Бернулли для идеальной жидкости

Выберем произвольно на рассматриваемом участке трубопровода два сечения: сечение 1-1 и сечение 2-2. Вверх по трубопроводу от первого сечения ко второму движется жидкость, расход которой равен Q,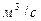

Для измерения пьезометрического давления жидкости применяют пьезометры - тонкостенные стеклянные трубки, в которых жидкость поднимается на высоту 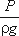. В каждом сечении установлены пьезометры, в которых уровень жидкости поднимается на разные высоты.

Кроме пьезометров в каждом сечении 1-1 и 2-2 установлена трубка, загнутый конец которой направлен навстречу потоку жидкости, которая называется трубка Пито.Трубка Пито предназначена для измерения полного напора жидкости в данном сечении. Жидкость в трубках Пито также поднимается на разные уровни, если отсчитывать их от пьезометрической линии.

Пьезометрическую линию можно построить следующим образом. Если между сечением 1-1 и 2-2 поставить несколько таких же пьезометров и через показания уровней жидкости в них провести кривую, то мы получим ломаную линию (рис.1).

Однако высота уровней в трубках Пито относительно произвольной горизонтальной прямой 0-0, называемой плоскостью сравнения, будет одинакова.

Если через показания уровней жидкости в трубках Пито провести линию, то она будет горизонтальна, и будет отражать уровень полной энергии трубопровода.

Запишем для двух произвольных сечений 1-1 и 2-2 потока идеальной жидкости уравнение Бернулли в форме напоров, т.е. каждый член уравнения имеет размерность :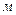

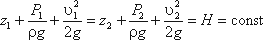
Так как сечения 1-1 и 2-2 взяты произвольно, то полученное уравнение можно переписать иначе:

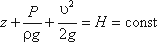
и прочитать так: сумма трех членов уравнения Бернулли для любого сечения потока идеальной жидкости есть величина постоянная.

С энергетической точки зрения каждый член уравнения представляет собой определенные виды энергии:

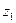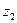и - удельные энергии положения единицы объема жидкости, характеризующие потенциальную энергию в сечениях 1-1 и 2-2;
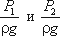- удельные энергии единицы объема жидкости, характеризующие потенциальную энергию в тех же сечениях;
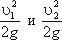- удельные кинетические энергии единицы объема жидкости, в тех же сечениях.

Следовательно, согласно уравнению Бернулли, полная удельная энергия идеальной жидкости в любом сечении постоянна, т.е. уравнение Бернулли – частный случай закона сохранения энергии.

Уравнение Бернулли можно истолковать и чисто геометрически. Дело в том, что каждый член уравнения имеет линейную размерность. Глядя на рис 1, можно заметить, что 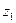и 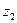- геометрические высоты сечений 1-1 и 2-2 над плоскостью сравнения; 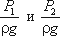- пьезометрические высоты; 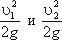- скоростные высоты в указанных сечениях. Так как каждый член уравнения измеряется в метрах, что очень удобно для построения пьезометрических графиков – геометрические высоты и удельные энергии можно изображать в масштабе графика.

В этом случае уравнение Бернулли можно прочитать так: сумма геометрической, пьезометрической и скоростной высоты для идеальной жидкости есть величина постоянная.

Уравнение Бернулли для реальной жидкости

Уравнение Бернулли для потока реальной жидкости несколько отличается от уравнения

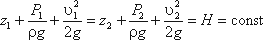
Дело в том, что при движении реальной вязкой жидкости возникают силы трения, на преодоление которых жидкость затрачивает энергию. В результате полная удельная энергия жидкости в сечении 1-1 будет больше полной удельной энергии в сечении 2-2 на величину потерянной энергии (рис. 2 ).

Потерянная энергия или потерянный напор обозначаются 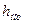и имеют также линейную размерность.

Уравнение Бернулли для реальной жидкости будет иметь вид:

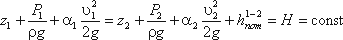
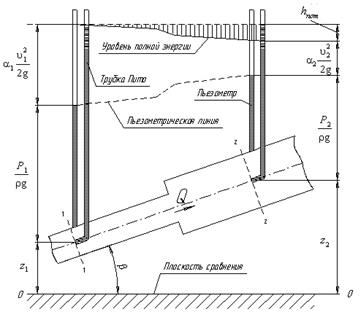
Рис. 2 . Схема к выводу уравнения Бернулли для реальной жидкости

Из рис. 2. видно, что по мере движения жидкости от сечения 1-1 до сечения 2-2 потерянный напор все время увеличивается (потерянный напор выделен вертикальной штриховкой). Таким образом, уровень первоначальной энергии, которой обладает жидкость в первом сечении, для второго сечения будет складываться из четырех составляющих: геометрической высоты, пьезометрической высоты, скоростной высоты и потерянного напора между сечениями 1-1 и 2-2.

Кроме этого в уравнении появились еще два коэффициента 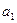и 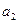, которые называются коэффициентами Кориолиса и зависят от режима течения жидкости ( 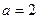для ламинарного режима, 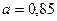для турбулентного режима ).

Потерянная высота 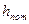складывается из линейных потерь, вызванных силой трения между слоями жидкости, и потерь, вызванных местными сопротивлениями (изменениями конфигурации потока)

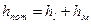
С помощью уравнения Бернулли решается большинство задач практической гидравлики. В тепловых сетях скоростной напор несоизмеримо меньше пьезометрического и мало изменяется по длине трубопровода. В таком случае, полный напор будет равен сумме геометрической высоты 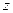и пьезометрического напора.

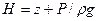
Потеря энергии на преодоление гидравлических сопротивлений 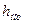определяется как разность полных напоров в начале и конце участка трубопровода.

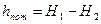
Пренебрегая скоростным напором 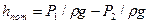, пьезометрический напор соответствует манометрическому давлению, и отсчитывается от оси трубопровода .Таким образом, пьезометрический напор определяется избыточным давлением в трубе и его максимальное значение определяется прочностью трубопровода.

Для определения скорости движения жидкости в трубопроводе

используют уравнение постоянства расхода для выбранных сечений трубопровода.

,

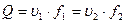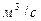
ОПИСАНИЕ УСТАНОВКИ

На (рис. 3.) дана конструктивная схема гидравлического стенда, вклю­чающего напорное и приемное устройства, измерительные прибо­ры и работай участок.

Основными элементами напорного устройства являются расходный- 1 и напорный - 2бачки. Положение напорного бачка по вы­соте может изменяться с помощью механизма подъема. Напор может изменяться от 1,46 до 2 метров. Напорный бачок 2 с трубкой-шлангом помещен в трубу 3.Верхний конец бачка 2 выполнен в виде воронки с выточками, через которые избыток воды перели­вается в трубу в сливную магистраль. В результате напор поддерживается постоянным. Расходный бачок 1 выполнен из нержавеющей стали в виде сферы достаточно большого размера, позволяющего получить ста­ционарный (установившийся) поток воды в рабочем участке 6.Расход воды через рабочий участок регулируется краном 9. Приемное устройство представляет из себя бак 12, связанный со сливной магистралью. Над приемным баком 12 на подвижной консоли 7 смонтирован мерный бачок 10, необходимый для измерения расхода воды. Консоль 7 имеет форму лотка и используется для слива воды в приемный бак 12.

Измерительные приборы представлены пьезометрическим щитом 4, на котором смонтированы стеклянные трубки длиной один метр. Стенд работает по замкнутой схеме, циркуляцию воды обеспечивает гидронасос 13, продувка контура от скопившегося воздуха осуществляется через патрубок 8. Общий объем воды в гидравлическом стенде, работающем по замкнутому циклу, составляет 60 литров.

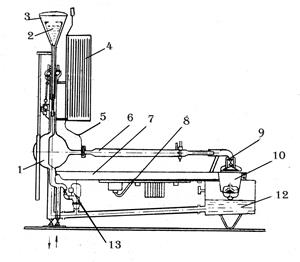
Рис. 3. Схема гидравлического стенда

Рабочий участок гидравлического стенда для данной лабораторной работы представляет собой трубу переменного сечения (рис.4). Для из­мерения статического давления жидкости в стенке трубы имеются отверстия с трубками, соединенны­ми с пьезометрами. Для измерения полного напора на оси трубы в тех же сечениях установлены изогнутые трубки Пито. Таким образом, разница столбиков жидкости полного и пьезометрического напора соответствует максимальному скоростному напору на оси трубы.

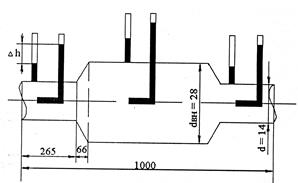
Рис.4. Схема рабочего участка установки

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Ознакомиться с установкой.

2. Подготовить журнал по форме (см. журнал наблюдений).

3. Включение гидравлического стенда осуществляется лаборантом.

4. Измерить пьезометрические и полные напоры во всех сечениях рабочего участка гидравлического стенда и занести их в журнал наблюдения. В нижнюю строку рабочего журнала записать истинное значение давления 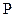в системе СИ, (1 мм водного столба соответствует 9,8 Па).

ОБРАБОТКА ОПЫТНЫХ ДАННЫХ

1. По показания трубки Пито и пьезометров рассчитать скоростные напоры для трех сечений рабочего участка трубы.

,

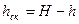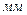
2. Определить средние скорости жидкости в измеряемых сечениях.

;

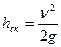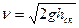
5. В масштабе построить пьезометрический график для вязкой жидкости по образцу рис.2

Результаты измерений потерь напора по длине на участке 1-2

№ п/п	Наименование	Обоз- нач.	Ед. измер	Сечения	При- меча-ние
	Показания пьезометров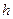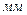
	Показания трубки Пито (полный напор)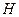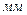
	Скоростной напор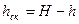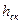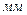
	Средняя скорость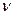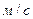
	Высота от поверхности трубопровода да начала пьезометрического щита.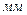

КОНТРОЛЬНЫЕ ВОПРОСЫ

1.Какие основные составляющие уравнения Бернулли?

2. Физический смысл составляющих уравнения Бернулли?

3. Что понимаем под геометрической трактовкой уравнения Бернулли?

4. Что называется коэффициентом Кориолиса?

5. В каких областях теплоэнергетики и для каких целей используется пьезометрический график?

ЛИТЕРАТУРА

1. Победря Б.Е., Георгиевский Д.В. Основы механики сплошной среды. - М., Физматлит, 2006 г.

2. Механика жидкости и газа под редакцией В.С. Швыдкого -

М., И.К.Ц., Академкника 2003 г

3. Калицун В.И. Основы гидравлики и аэродинамики – М., Стройиздат, 2001г