Тема: Элементы теории корреляции

Объекты ряда генеральных совокупностей обладают несколькими подлежащими изучению признаками Х, У, ..., которые можно интерпретировать как систему взаимосвязанных величин. Примерами могут служить: масса животного и количество гемоглабина в крови, рост мужчины и объем грудной клетки, увеличение рабочих мест в помещении и уровень заболеваемости вирусными инфекциями, количество вводимого препарата и концентрация его в крови и т.д.

Очевидно, что между этими величинами существует связь, но она не может быть строгой фукциональной зависимостью, так как на изменение одной из величин влияет не только изменение второй величины, но и другие факторы. В таких случаях говорят, что две величины связаны стохастической (т.е. случайной) зависимостью. Мы будем изучать частный случай стохастической зависимости – корреляционную зависимость.

ОПРЕДЕЛЕНИЕ: Зависимость случайных величин называют стохастической, если на изменение одной из них влияет не только изменение второй величины, но и другие факторы.

ОПРЕДЕЛЕНИЕ: Зависимость случайных величин называют статистической, если изменения одной из них приводит к изменению закона распределения другой.

ОПРЕДЕЛЕНИЕ:Если изменение одной из случайных величин влечет изменение среднего другой случайной величины, то статистическую зависимость называют корреляционной.

Примерами корреляционной зависимостиявляются связи между:

- массой тела и ростом;

- дозой ионизирующего излучения и числом мутаций;

- пигментом волос человека и цветом глаз;

- показателями уровня жизни населения и процентом смертности;

- количеством пропущенных студентами лекций и оценкой на экзамене и т.д.

Именно корреляционные зависимости наиболее часто встречаются в природе в силу взаимовлияния и тесного переплетения огромного множества самых различных факторов, определяющих значения изучаемых показателей.

Результаты наблюдения, проведенные над тем или иным биологическим объктом по корреляционно связанным признакам У и Х можно изобразить точками на плоскости, построив систему прямоугольных координат. В результате получается некая диаграмма рассеяния, позволяющая судить о форме и тесноте связи между варьирующими признаками.

Если эту связь можно будет апроксимировать некоторой кривой, то можно будет прогнозировать изменение одного из параметров при целенаправленном изменении другого параметра.

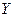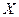Корреляционную зависимость от можно описать с помощью уравнения вида

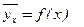(1)

где 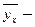условное среднее величины 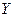, соответствующее значению 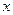величины 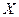, а 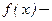некоторая функция. Уравнение (1) называется выборочным уравнением регрессии 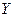на .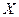

Рис.1. Линейная регрессия значима. Модель .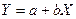

Функцию 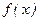называют выборочной регрессией 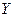на 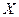, а ее график – выборочной линией регрессии 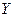на .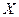

Совершенно аналогично выборочным уравнением регрессии 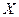на 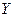является уравнение .

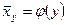В зависимости от вида уравнения регрессии и формы соответствующей линии регрессии определяют форму корреляционной зависимости между рассматриваемыми величинами – линейной, квадратической, показательной, экспоненциальной.

Важнейшим является вопрос выбора вида функции регресси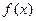и [или 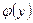], например линейная или нелинейная (показательная, логарифмическая и т.д.)

На практике вид функции регрессии можно определить построив на координатной плоскости множество точек, соответствующих всем имеющимся парам наблюдений ( ).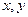

Рис. 2. Линейная регрессия незначима. Модель .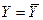

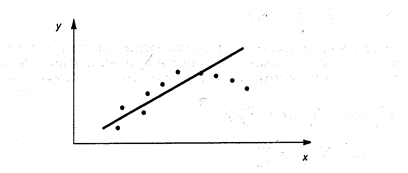Рис. 3. Нелинейная модель .

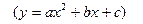Например, на рис.1. видна тенденция роста значений 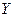с ростом 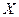, при этом средние значения 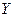располагается визуально на прямой. Имеет смысл использовать линейную модель (вид зависимости 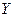от 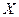принято называть моделью) зависимости 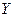от .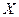

На рис.2. средние значения 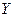не зависят от 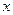, следовательно линейная регрессия незначима (функция регрессии постоянна и равна ).

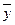На рис. 3. прослеживается тенденция нелинейности модели.

Примеры прямолинейной зависимости:

- увеличение количество потребляемого йода и снижение показателя заболеваемости зобом,

- увеличение стажа рабочего и повышение производительности.

Примеры криволинейной зависимости:

- с увеличением осадков – увеличивается урожай, но это происходит до определенного предела осадков. После критической точки осадки уже оказываются излишними, почва заболачивается и урожай снижается,

- связь между дозой хлора, примененной для обеззараживания воды и количеством бактерий в 1 мл. воды. С увеличением дозы хлора количество бактерий в воде снижается, но по достижению критической точки количество бактерий будет оставаться постоянным (или совсем отсутствовать), как бы мы не увеличивали дозу хлора.

Линейная регрессия

Выбрав вид функции регрессии, т.е. вид рассматриваемой модели зависимости 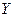от Х (или Х от У), например, линейную модель 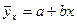, необходимо определить конкретные значения коэффициентов модели.

При различных значениях а и 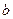можно построить бесконечное число зависимостей вида 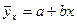т.е на координатной плоскости имеется бесконечное количество прямых, нам же необходима такая зависимость, которая соответствует наблюдаемым значениям наилучшим образом. Таким образом, задача сводится к подбору наилучших коэффициентов.

Метод наименьших квадратов (МНК)

Линейную функцию 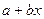ищем, исходя лишь из некоторого количества имеющихся наблюдений. Для нахождения функции с наилучшим соответствием наблюдаемым значениям используем метод наименьших квадратов.

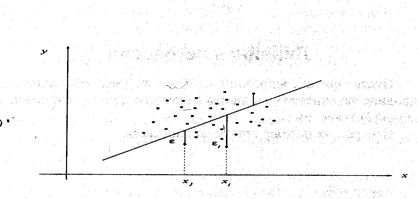
Рис.4. Пояснение к оценке коэффициентов методом наименьших квадратов

Обозначим: 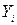- значение, вычисленное по уравнению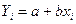

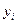- измеренное значение,

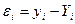- разность между измеренными и вычисленными по уравнению значениям,

.

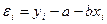Вметоде наименьших квадратов требуется, чтобы 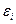, разность между измеренными 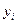и вычисленными по уравнению значениям 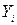, была минимальной. Следовательно, находимо подобрать коэффициенты а и 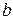так, чтобы сумма квадратов отклонений наблюдаемых значений от значений на прямой линии регрессии оказалась наименьшей:

.

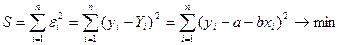Это условие достигается если параметры а и 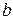будут вычислены по формулам :

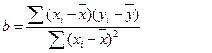(2)

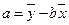
(3)

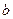называют коэффициентом регрессии; 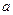называют свободным членомуравнения регрессии.

Полученная прямая является оценкой для теоретической линии регрессии. Имеем

.

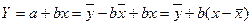Итак, 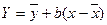является уравнением линейной регрессии.

Регрессия может быть прямой 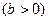и обратной .

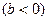ОПРЕДЕЛЕНИЕ: Обратная регрессия означает, что при росте одного параметра, значения другого параметра уменьшаются.

ОПРЕДЕЛЕНИЕ: Прямая регрессия означает, что при росте одного параметра, значения другого параметра тоже увеличиваются.

Пример 1.Заданному уровню потребления пресной воды на санитарно – бытовые нужды 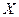в л/чел. сутки в n населенных пунктах соответствует множество значений уровня общей заболеваемости 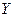в %. При этом отмечается, что с ростом 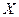наблюдается уменьшение 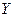. Это – обратная, отрицательнаякорреляционная связь. (Рис. 5)

Пример 2.Возрастание уровня инфекционной заболеваемости 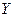в % при увеличении плотности рабочих мест в производственном помещении 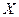, чел. – является примером прямой, положительной корреляционной связи. (Рис. 6)

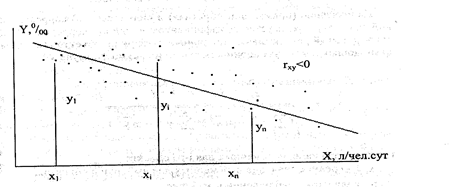Рис. 5. Поле наблюдений 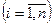при обратной корреляционной

связи между фактором 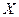и параметром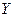

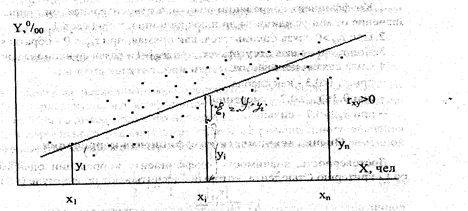Рис. 6. Поле наблюдений 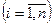при прямой корреляционной

связи между фактором 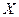и параметром