Где а - положительное число

Наша з а д а ч а - найти функцию u(x,t) , график которой дает форму струны в любой момент времени t, т. е. найти решение уравнения (1) при граничных:

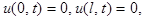(2)

и начальных условиях:

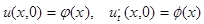(3)

Сначала будем искать решения уравнения (1), удовлетворяющие граничным условиям(2). Нетрудно увидеть, что u(x,t) 0 является решением уравнения (1), удовлетворяющие граничным условиям(2). Будем искать решения, не равные тождественно 0, представимые в виде произведения u(x,t)=X(x)T(t), (4) , где , .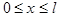

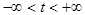Подстановка выражения (4) в уравнение (1) дает:

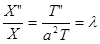
Из которого наша задача сводится к отысканию решений уравнений:

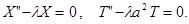
Используя это условие X(0)=0, X(l)=0, докажем, что 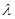отрицательное число, разобрав все случаи.

a) Пусть 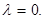Тогда X”=0 и его общее решение запишется так:

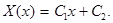
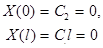
откуда 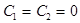и 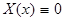,что невозможно , так как мы рассматриваем решения, не обращающиеся тождественно в нуль.

б) Пусть 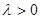. Тогда решив уравнение

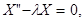
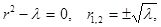
получим 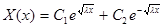, и, подчинив, найдем, что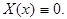

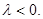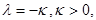в) Если то

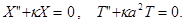
Уравнения имеют корни :

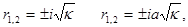
получим:

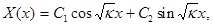
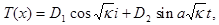
где 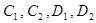-произвольные постоянные. Из начального условия найдем:

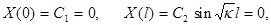
откуда 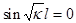, т. е.

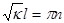(n=1,2,...)

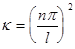(n=1,2,...).

Учитывая это, можно записать:

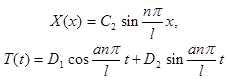(n=1,2,...).

и, следовательно

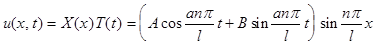, (n=1,2,...),

но так как A и B разные для различных значений n то имеем

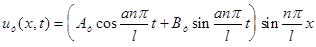, (n=1,2,...),

где 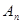и 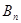произвольные постоянные, которые попытаемся определить таким образом, чтобы ряд удовлетворял уравнению (1), граничным условиям (2) и начальным условиям (3).

Итак, подчиним функцию u(x,t) начальным условиям, т. е. подберем 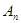и 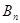так , чтобы выполнялись условия

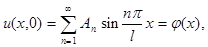
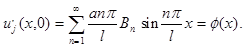
Эти равенства являются соответственно разложениями функци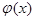й и 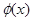на отрезки [0, l] в ряд Фурье по синусам. ( Это значит что коэффициенты будут вычисляться как для нечетной функций). Таким образом, решение о колебании струны с заданным граничными и начальными условиями дается формулой

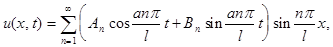
где

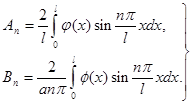(n=1,2,...)

Интеграл Фурье

Достаточные условия представимости функции в интеграл Фурье.

Для того, чтобы f(x) была представлена интегралом Фурье во всех точках непрерывности и правильных точках разрыва, достаточно:

1) абсолютной интегрируемости на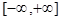

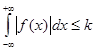(т.е. интеграл сходится)

2) на любом конечном отрезке [-L, L] функция была бы кусочно-гладкой

3) в точках разрыва функции, ее интеграл Фурье определяется полусуммой левого и правого пределов в этих точках, а в точках непрерывности к самой функции f(x)

Интегралом Фурье функции f(x) называется интеграл вида:

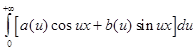
, где ,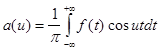

.

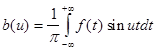Интеграл Фурье для четной и нечетной функции

Пусть f(x)-четная функция, удовлетворяющая условиям представимости интегралом Фурье.

Учитывая, что 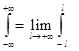, а также свойство интегралов по симметричному относительно точки x=0 интервалу от четных функций, из равенства (2) получаем:

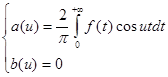(3)

Таким образом, интеграл Фурье четной функции f(x) запишется так:

,

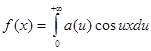где a(u) определяется равенством (3).

Рассуждая аналогично, получим, для нечетной функции f(x) :

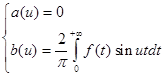(4)

и, следовательно, интеграл Фурье нечетной функции имеет вид:

,

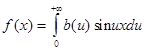где b(u) определяется равенством (4).

Комплексная форма интеграла Фурье

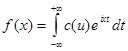, (5)

где

.

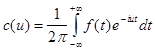Выражение в форме (5) является комплексной формой интеграла Фурье для функции f(x).

Если в формуле (5) заменить c(u) его выражением, то получим:

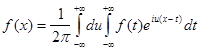, где правая часть формулы называется двойным интегралом

Фуpье в комплексной форме. Переход от интеграла Фурье в комплексной форме к интегралу

в действительной форме и обратно осуществим с помощью формул:

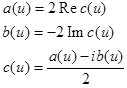
Формулы дискретного преобразования Фурье

Обратное преобразование Фурье.

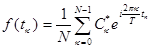
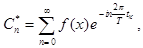
где n=1,2,... , k=1,2,...

Дискретным преобразованием Фурье - называется N-мерный вектор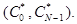

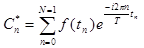
при этом, 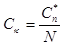.