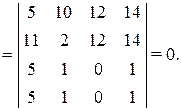Определители произвольного порядка

ВВЕДЕНИЕ

Настоящие методические указания предназначены для студентов всех специальностей и направлений бакалаврской подготовки заочной формы обучения, выполняющих расчетно-графическую работу по линейной алгебре, аналитической геометрии и введению в анализ. Приведенные краткие теоретические сведения, типовые задачи и примеры по каждому разделу позволяют успешно справиться с аналогическими заданиями самостоятельно и способствуют формированию предметного представления о соотношении теоретических и практических результатов.

ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЕЙ

Определители второго порядка

Определителем второго порядка 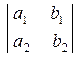называется число:

.

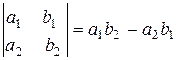Определение показывает несложность вычисления определителей второго порядка.

Примеры.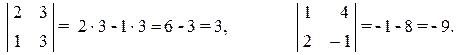

Определители третьего порядка

Определителем третьего порядка 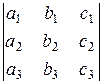называется число, которое может быть вычислено по следующему правилу (правило Саррюса): к определителю справа приписывается первый и второй столбцы и элементы, стоящие на диагоналях полученной таблицы, перемножаются, а затем эти произведения складываются, причем произведения элементов на диагоналях, идущих снизу вверх, берутся со знаком минус:

_.

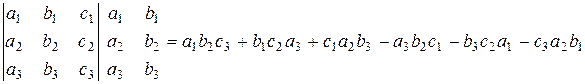Примеры.

а) -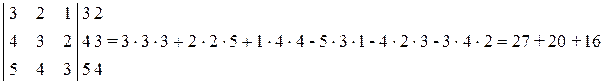

-15-24-24=0

б)

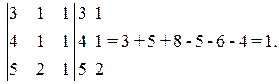
Задачи для самостоятельного решения

Вычислить определители второго и третьего порядка:

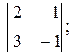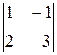а) б) ; в)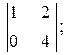

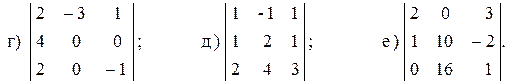
Определители произвольного порядка

Пусть задан определитель n-го порядка

.

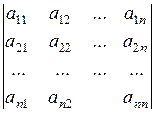Для любого определителя выполнены свойства:

а) если в определителе две строки или два столбца равны, то определитель равен нулю:

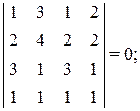
б) если в определителе какая-либо строка или столбец состоит из нулей, то этот определитель равен нулю:

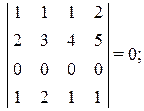
в) общий множитель в строке или столбце можно вынести за знак определителя:

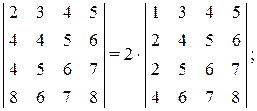
г) если в определителе поменять местами две строки или два столбца, то определитель изменит знак:

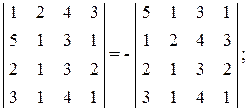
д) определитель не изменится, если к произвольной строке прибавить другую строку, домноженную на любое число. Это же справедливо и для столбцов. Например, в следующем определителе к третьей строке добавлена первая, домноженная на минус два:

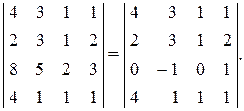
Для вычисления определителей специального треугольного вида применимо следующее правило:

_.

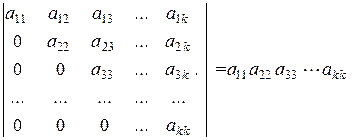Свойства определителей позволяют любой определитель свести к треугольному виду и вычислить его по указанному правилу.

Примеры.

а) 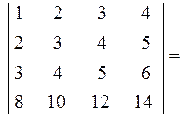(ко второй строке прибавляем первую, домноженную на (-2), к третьей строке прибавляем первую, домноженную на (-3), к четвертой строке прибавляем первую, домноженную на (-8))

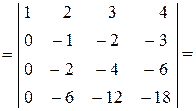(к третьей строке прибавляем вторую, домноженную на (-2))

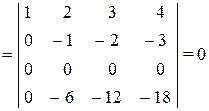(по второму свойству определителей).

б) 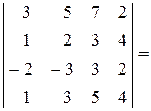(поменяем вторую и первую строки местами, чтобы иметь единицу на первом месте в первой строке) =

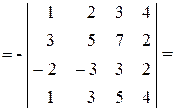(ко второй строке прибавляем первую, домноженную на (-3) и т.д.) =

.

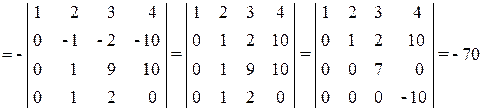в) 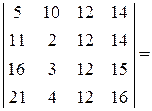(к третьей строке прибавляем вторую, домноженную на (-1), к четвертой строке прибавляем третью, домноженную на (-1), для уменьшения чисел в первом столбце)