Пример выполнения задания. Даны: m = 0,4 кг; uА = 0; tВD = 0,3 с; f = 0,3; h0 =40 см; с = 0,7 Н/см; R = 0,5 м; a = 45°; b = 30°

Даны: m = 0,4 кг; u_А = 0; t_ВD = 0,3 с; f = 0,3; h₀ =40 см; с = 0,7 Н/см; R = 0,5 м; a = 45°; b = 30°. Схема механизма показана на рисунке 10а. Определить u_В, u_С, u_D и N_C.

Решение. Проанализируем движение шарика на всем пути АС. На всем участке АС на шарик действуют сила тяжести G и нормальная реакция стенки трубки N’. На участке АD дополнительно действует сила трения скольжения F_тр (на дуге DC ею пренебрегаем), а на участке АВ помимо указанных сил действует сила упругости пружины Р. В связи с этим рассмотрим движение шарика поэтапно на участках АВ, BD и DC.

Для определения скоростей в точках B, С и D будем применять следующие теоремы: 1) об изменении количества движения материальной точки; 2) об изменении кинетической энергии материальной точки. Проанализировав уравнения этих теорем, можно сделать вывод, что по составу величин они отличаются только левыми частями: в первом уравнении содержится время прохождения участка, а во втором – длина участка или высота подъема (спуска). Поэтому при выборе той или иной теоремы необходимо опираться на начальные данные.

1. Определение скорости u_В. Как уже упоминалось ранее, на участке АВ движение шарика происходит под действием сил G, N’, F_тр и Р (рисунок 10б). Поскольку известна длина участка АВ = h₀ и неизвестно время его прохождения, то для нахождения скорости шарика в точке В u_В воспользуемся теоремой об изменении кинетической энергии материальной точки:

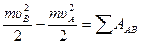, (23)

где SА_АВ – сумма работ всех сил, действующих на точку на участке АВ.

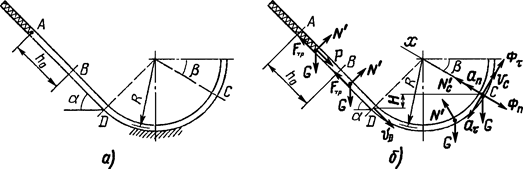
Рисунок 10 – Схема механизма (а) и расчетная схема (б)

Определим работы сил. Работа силы тяжести:

;

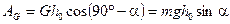работа нормальной реакции A_N’ = 0, так как ;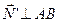

работа силы трения: .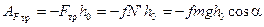

Так как сила упругости пружины переменна и по закону Гука равна P = cx, где х – текущая деформация пружины, то работа этой силы на участке АВ:

.

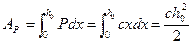Тогда .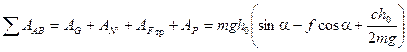

Подставив это выражение в уравнение (23) получим: .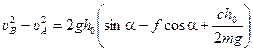

Так как u_А= 0, то 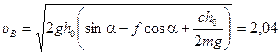м/с.

2. Определение скорости u_D. На участке BD движение шарика происходит под действием сил G, N’ и F_тр (рисунок 10б). Поскольку известно время прохождения участка t_ВD и неизвестна его длина, то для нахождения скорости шарика u_D воспользуемся теоремой об изменении количества движения материальной точки:

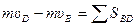, (24)

где SS_BD – сумма импульсов всех сил, действующих на шарик на участке ВD.

Определим импульсы сил на участке BD. Импульс силы тяжести:

;

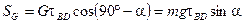импульс нормальной реакции S_N’ = 0, так как ;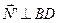

импульс силы трения .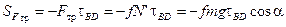

Тогда .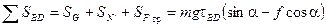

Подставив это выражение в уравнение (24), получим:

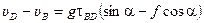, откуда 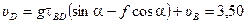м/с.

3. Определение скорости u_С. На криволинейном участке DС движение шарика происходит под действием сил G, и N’ (рисунок 10б). Так как известны геометрические размеры участка DC, но неизвестно время его прохождения, то для нахождения скорости шарика в точке С воспользуемся теоремой об изменении кинетической энергии материальной точки:

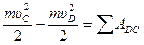, (25)

где SА_DC – сумма работ всех сил, действующих на точку на участке DC.

Определим работы сил. Работа силы тяжести на участке DC:

;

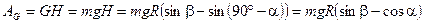работа нормальной реакции A_N’ = 0, так как реакция 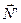на всем пути DC перпендикулярна направлению движения ( 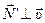). Тогда

.

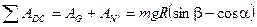Подставив это выражение в уравнение (25), получим:

,

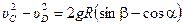откуда 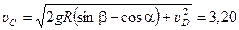м/с.

4. Определение силы давления шарика на стенку трубки N_С. Для нахождения давления шарика в положении С воспользуемся принципом Даламбера для материальной точки, в соответствии с которым геометрическая сумма сил, приложенных к точке, с учетом силы инерции этой точки 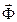равна нулю: .

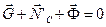Силу инерции шарика можно разложить на нормальную и касательную составляющие (рисунок 10б): .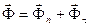

Сумма проекций сил 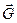, 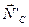и 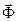на ось х, нормальную направлению движения, должна быть равна нулю (рисунок 10б):

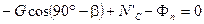или 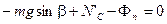, (26)

где 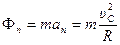. Тогда из уравнения (26) 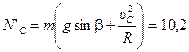Н.

Искомая сила давления N_C шарика на стенку трубки по модулю равна нормальной реакции 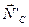и направлена противоположно ей.

Задание Д.10. Применение теоремы об изменении кинетической