Некоторые теоремы о дифференцируемых функциях
- Теорема о корнях производной (теорема Ролля)
Если функция y=f(x) непрерывна и дифференцируема на отрезке [a,b] и на концах отрезка f(a)=f(b)=0, то существует внутри отрезка [a,b] по крайней мере одна точка x=c, a<c<b, в которой производная f’(x) обращается в 0.
Доказательство
Так как f(x) непрерывна на [a,b], то она имеет на этом отрезке наибольшее (М) и наименьшее (m) значения.
Если M=m, то f(x) постоянна, то есть при всех значениях х - f(x)=0 и для 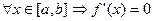 . Теорема доказана.
. Теорема доказана.
Если 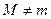 , то, полагая M>0 и f(x) принимает наибольшее значение при х=с, то есть f(c)=M, при этом
, то, полагая M>0 и f(x) принимает наибольшее значение при х=с, то есть f(c)=M, при этом 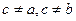 , так как по условию f(a)=f(b)=0
, так как по условию f(a)=f(b)=0
Учитывая, что f(c) - наибольшее значение функции, то 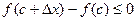 при
при 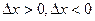 . Отсюда следует
. Отсюда следует
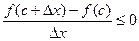 , при
, при 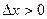 (1')
(1')
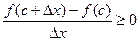 , при
, при 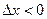 (1’’)
(1’’)
Так как по условию теоремы f’(x) существует при х=с, то переходя к пределу при 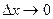 получим
получим
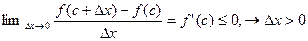
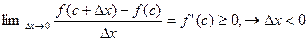
Но соотношения 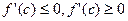 совместимы лишь в том случае, когда f’(c)=0. Следовательно, внутри отрезка [a,b] имеется точка с, в которой f’(c)=0.
совместимы лишь в том случае, когда f’(c)=0. Следовательно, внутри отрезка [a,b] имеется точка с, в которой f’(c)=0.
Геометрическая интерпретация
Если непрерывная кривая, имеющая в каждой точке касательную, пересекается с осью ОХ в точках x=a,x=b, то на этой кривой найдется, по крайней мере одна точка с абсциссой x=c, a<c<b, в которой касательная параллельна оси ОХ.
- Теорема о конечных приращениях (теорема Лагранжа)
Если y=f(x) непрерывна и дифференцируема на отрезке [a,b], то внутри отрезка [a,b] найдется, по крайней мере, одна точка c, a<c<b, что
f(b)-f(a)=f’(c)(b-a) (1)
Доказательство
Обозначим 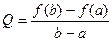 (2)
(2)
Рассмотрим вспомогательную функцию F(x)=f(x)-f(a)-(x-a)Q (3)
Геометрический смысл F(x) следующий:
Напишем уравнение хорды AB. Учитывая, что ее угловой коэффициент равен 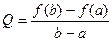 и, что она проходит через точку (a,f(a)).
и, что она проходит через точку (a,f(a)).
y-f(a)=Q(x-a) 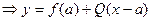 , но F(x)=f(x)-[f(a)+Q(x-a)]
, но F(x)=f(x)-[f(a)+Q(x-a)]
следовательно, F(x) для каждого значения х равняется разности ординат кривой f(x) и хорды y=f(a)+Q(x-a) для точек с одинаковой абсциссой.
Так как F(x) непрерывна и дифференцируема на [a,b] и F(a)=F(b)=0, то к ней можно применить теорему Ролля, согласно которой существует точка 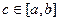 , что F’(c)=0. Но F’(x)=f’(x)-Q
, что F’(c)=0. Но F’(x)=f’(x)-Q 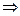 F’(c)=f’(c)-Q=0
F’(c)=f’(c)-Q=0 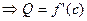 . Подставляя это в равенство (2) получаем
. Подставляя это в равенство (2) получаем 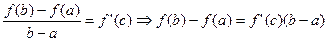 . Теорема доказана.
. Теорема доказана.
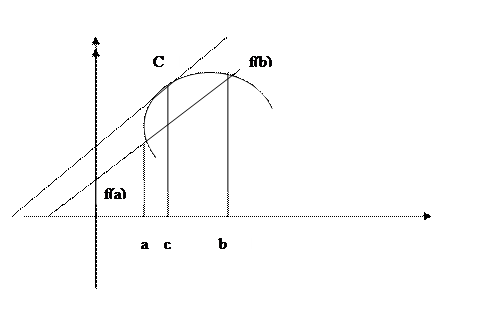
Геометрическая интерпретация
Если во всех точках дуги AB существует касательная, то существует точка с, в которой касательная параллельна хорде AB.
- Теорема об отношении приращений двух функций (теорема Коши)
Если 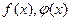 непрерывные и дифференцируемые функции на отрезке [a,b], причем
непрерывные и дифференцируемые функции на отрезке [a,b], причем 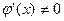 , при
, при 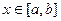 , то найдется такая точка x=c, a<c<b, что
, то найдется такая точка x=c, a<c<b, что 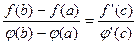 (1)
(1)
Доказательство
Обозначим 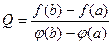 (2)
(2)
Отметим, что 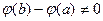 , так как в противном случае по теореме Ролля
, так как в противном случае по теореме Ролля 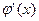 обращалась бы в 0 внутри отрезка [a,b], что противоречит условию теоремы.
обращалась бы в 0 внутри отрезка [a,b], что противоречит условию теоремы.
Составим вспомогательную функцию F(x)=f(x)-f(a)-Q 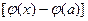 (3). Так как F(x) непрерывна и дифференцируема на [a,b] и F(a)=F(b)=0, то к ней можно применить теорему Ролля, согласно которой существует точка
(3). Так как F(x) непрерывна и дифференцируема на [a,b] и F(a)=F(b)=0, то к ней можно применить теорему Ролля, согласно которой существует точка 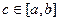 , что F’(c)=0.
, что F’(c)=0.
Но F’(x)=f’(x)-Q 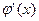
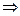 F’(c)=f’(c)-Q
F’(c)=f’(c)-Q 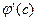 =0
=0 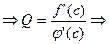
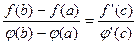 . Теорема доказана.
. Теорема доказана.
