Ерекше емес диагональдыҚ, ҮшбҰрышты матрицалар группасы

3.1 Бейнелеулер, функциялар, операторлар.

Бейнелеу, функция, оператор сөздерінің бәрінің мағынасы бір – яғни жиынының әрбір элементіне оған бірмәнді анықталған жиынына тиісті элементі сәйкес қойылады. Бұл ереженің берілуі 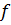бейнелеудің (функцияның, оператордың) графигі деп аталатын

ішкі жиынын таңдап алуға тепе-тең.

элементі элементінің бейнесі деп, ал – элементінің 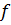бейнелеуіндегі түп бейнесі деп аталады. 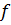– -ті -ке бейнелейді дегенді былай жазады: .

жиыны 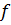бейнелеуінің бейнесі (мәндер жиыны) деп аталады.

Егер болса, онда жиыны жиынынң толық түп бейнесі деп аталады. Егер болса, онда .

бейнелеуі қайтымды деп аталады, егер және болатындай бейнелеуі бар болатын болса. Сонымен қатар, -ді -ке кері бейнелеу деп атайды және оны деп жазады.

Егер кез келген үшін толық түп бейне тек бір ғана элементтен құралса, онда бейнелеуі өзара – бірмәнді деп аталады.

2.2 Алгебралық амалдар

бейнелеуі -қа алгебралық амал деп аталады. Айталық мұндай амалды белгілеу үшін * символы қолданылсын. Онда жазбасы және дегенді білдіреді.

Егер құр емес ішкі жиында бейнелеуі берілсе, онда -ті -ке бөліктей алгебралық амалдар деп аталады. Дербес жағдайда мұндай амалдарға матрицаларды барлық матрицалар жиынына көбейту амалы жатады.

2.3 Ассоциативтілік және жақшалар

Егер кез келген үшін және көбейтінділерінің бар болуынан көбейтінділері және теңдігінің бар болатындығы шығатын болса, онда -ке бөліктей алгебралық амалдар ассоциативті деп аталады. Бұл жағдайда жақшаларды алып тастап, былай жазуға болады: .

Теорема. Айталық - та ассоциативті бөліктей алгебралық амалдар берілсін және кез келген элементтері үшін көбейтінділері бар болсын. Онда

элементін анықтайтын жақшалардың қойылуы бар болады, сонымен қатар жақшаларды кез келген етіп қойған жағдайда сол бір ғана элементін береді.

Дәлелдеуі. бойынша индукцияны қолданайық. Алдымен -ті анықтайтын қандай да бір жақшаның қойылуының бар болатындығын дәлелдейік. Индуктивті ұйғарым бойынша, көбейтінді бар болады. теореманың шарты бойынша, сондай-ақ, көбейтіндісі де бар болады. Осылайша, элементтеріне қатысты ассоциативтіліктің анықтамасын қолдануға болады.

Айталық элементтері жақшалар әр түрлі қойылған жағдайда алынсын. Сонда да мынаны аламыз:

Айталық болсын. Онда ассоциативтіліктің анықтамасының негізінде былай болады:

2.4 Матрицаларды көбейтудегі ассоциативтілік

Айталық өлшемді үш тікбұрышты матрицалардың көбейтіндісін есептеу керек болсын:

Берілген жағдайда жақшаларды қоюдың екі нұсқасы бар:

(1)мен (2) нұсқалар матрицасын екі әртүрлі есептеу алгоритміне әкеледі. Ассоциативтіліктің негізінде нәтижелер бірдей болуы керек.

2.5 Группалар

Ассоциативті алгебралық амалдар анықталған құр емес жиыны группа деп аталады, егер

1. болатындай кез келген элементі үшін элементі бар болады;

2. болатындай кез келген элементі үшін элементі бар болады.

элементі (1) қасиет бойынша бірмәнді анықталады: егер және – екі осындай элемент болса, онда болады. элементі элементіне кері деп аталады және оны деп белгілейді.

Группа абельдік (коммуттативті) деп аталады, егер барлық үшін болатын болса.