Вторая производная функции , заданной параметрически

Рассмотрим уравнение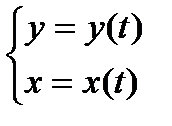

где 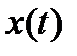, 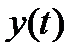− дважды дифференцируемые функции на некотором промежутке 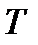; пусть, кроме того, функция 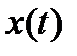строго возрастает (или убывает) на 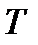и ни в одной точке этого промежутка 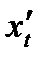не равна 0. В пункте 20.7 доказано, что в этом случае уравнения (2) задают функцию 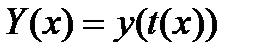, и производная этой функции равна

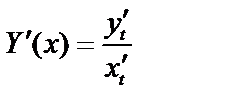
Бывает также, что производные по параметру 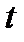обозначают так: 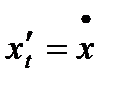, 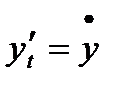. Тогда формула (3) принимает вид: 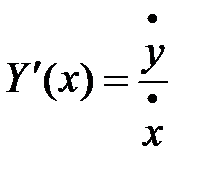. Найдём вторую производную функции :

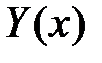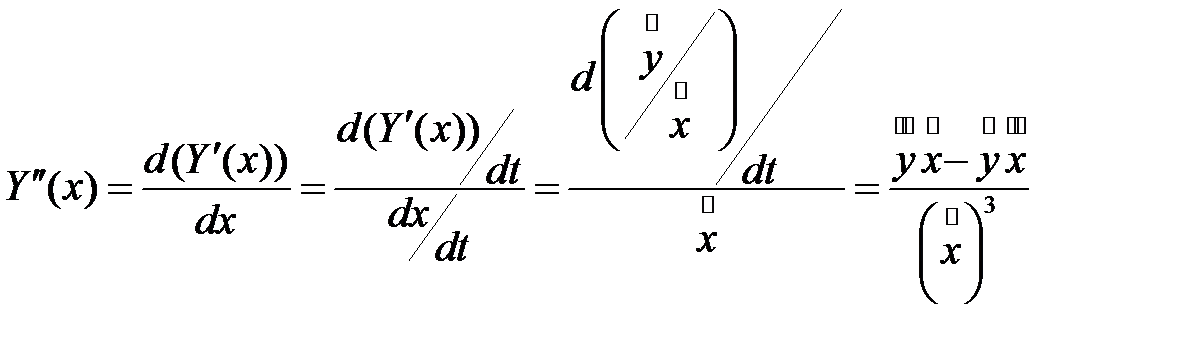
ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ

Однородную линейную функцию называют линейной формой.

Напомним, что если функция 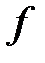дифференцируема в точке 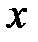, то

дифференциалом 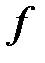в x называют линейную форму .

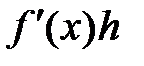Аналогично, если 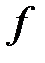дифференцируема дважды в точке ,

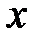то ее вторым дифференциалом называют квадратичную форму .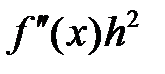

Вообще, n-ым дифференциалом 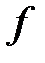в точке x будет n-ичная

форма 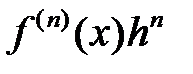(в предположении, что 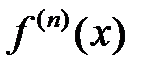существует).

Для n-го дифференциала 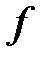в точке x используют обозначение 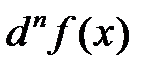или, более

строго .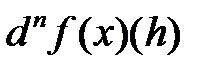

Таким образом, по определению,

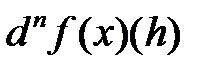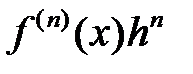= для всех 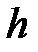Î .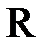

Согласно этому определению, 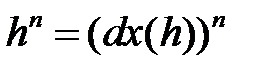есть n-я степень функци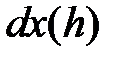и и

потому используют обозначение 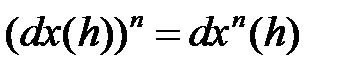. Тогда

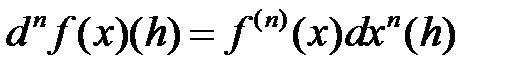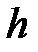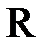для всех Î , или

.

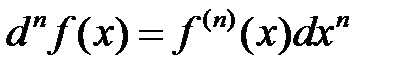Форма записи n-го дифференциала не инвариантна

уже при n=2. Действительно, подставляя вместо 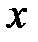дифференцируемую

функцию 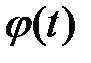в левую часть формулы (при n=2), получим

=

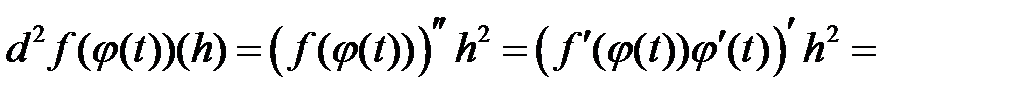
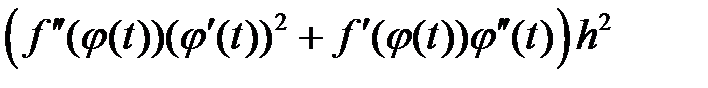
а в результате такой же подстановки в правую часть, имеем

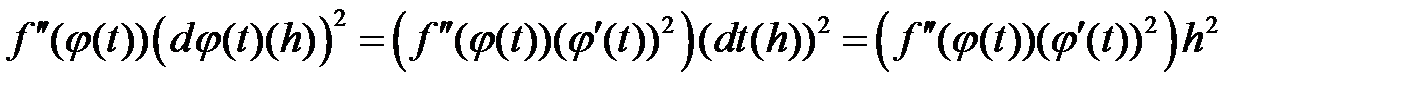.(5)

Правые части этих формул отличаются слагаемым .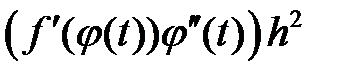

Вообще говоря, это слагаемое не равно нулю. Однако если 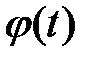- линейная функция,

то 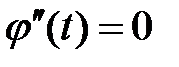и, вообще, для любого 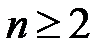имеет место равенство ,

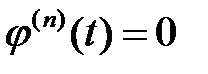откуда следует, что формула будет верна и для линейной функции .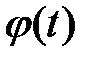

ЭЛАСТИЧНОСТЬ И ЕЁ СВОЙСТВА

Определение. Пусть функция y определена в некоторой окрестности точки x, дифференцируема в точке x и y(x) ≠ 0. Эластичностью функции y в точке x называется величина

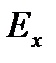(y) =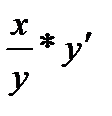

Если предположить, что x 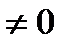, то можно рассматривать величину

,

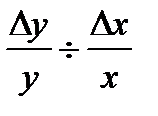которая характеризует величину относительного изменения y в результате соответствующего относительного изменения x; например, процентное изменение спроса на товар в результате однопроцентного изменения цены этого товара. Тогда следует, что

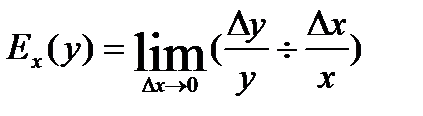
Если y>0, то 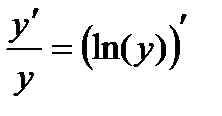по теореме о производной сложной функции.

Если y<0, то ,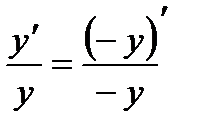

поэтому при y<0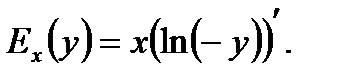

Следовательно,

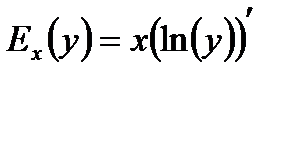при y>0

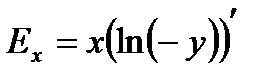при y<0

Обе эти формулы можно объединить в одну :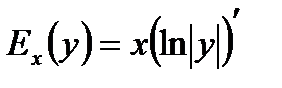

Теорема. 1) Если u, v – функции, для которых определены эластичности и ,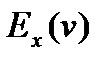

То: = +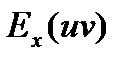

- .

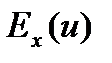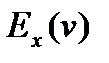
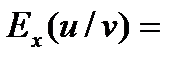
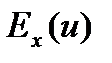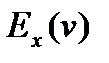2) Если для функции y = y(x), определённой на интервале 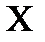, существует обратная функция x = x(y), причём y дифференцируема на этом интервале 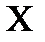и ни в одной точке x интервала не выполняется равенство 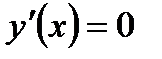, то для всех x 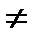0, y 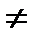0 определены величины 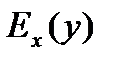и ,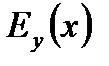

причём 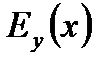= .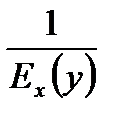