Проверяем правильность вычисления опорных реакций (сумма проекций всех сил на вертикальную ось z должна быть равна 0)

S F_z = R_A + Rq₁ – Rq₂+ R_B – F = (– 4,1кН) + 12кН – 15кН +14,1кН – 7кН =

= 26,1кН –26,1кН = 0.

2. Построение эпюр поперечных сил Q и изгибающего моментов M

В нашем примере балка имеет три участка, которые пронумеруем слева направо (рис.13). Проводим сечение на I участке и рассматриваем левую от сечения часть балки (рис.13), т.к. слева от сечения сил приложено меньше, чем справа.

Рис.13

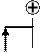I участок 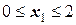(начало отсчета на левом конце балки);

Q(x₁) = R_A + q₁ x₁= – 4,1кН+ 6кН/м·x₁;

Q(0) = – 4,1кН+ 6кН/м·0= – 4,1кН (значение на левой границе участка);

Q(2м) = – 4,1кН + 6кН/м·2м= 7,9кН (значение на правой границе участка).

Поскольку поперечная сила меняет знак в пределах участка, определяем координату, при которой она обращается в нуль:

Q(x₀) = – 4,1кН+ 6кН/м·x₀=0; x₀= 0,683333 м=0,683 м;

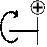Переходим к определению изгибающего момента на Iучастке

M (x₁) = R_Ax₁ + 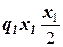= – 4,1кН·x₁+ 6 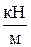· 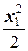= – 4,1кН·x₁+ 3кН/м·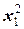

Слева от сечения моменты всех сил берем относительно точки С₁(центр тяжести поперечного сечения – рис.13).

Изгибающий момент (M) является квадратичной функцией координаты x₁.

Для построения его графика определяем значение изгибающего моментана границах участка и в найденной выше точке.

M (0) = – 4,1кН·0+ 3кН/м· 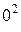=0 (значение на левой границе участка);

M (0,683м) = – 4,1кН ·0,683м+ 3кН/м·(0,683м )² = – 1,40кНм;

M (2м) = – 4,1кН·2м+ 3кН/м·(2м )² = 3,8 кНм (значение на правой границе).

Проводим сечение на II участке и рассматриваем правую от сечения часть балки (рис.13).

II участок 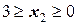(начало отсчета на правой границе участка);

Q(x₂) = F– R_B – q₂·x₂= 7кН–14,1кН+ 5кН/м·x₂ = –7,1кН+ 5кН/м·x₂;

Обратите внимание, что учитываются все силы, действующие справа от сечения, положительное направление силы справа от сечения – вниз.

Q(0) = –7,1кН+ 5кН/м·0= –7,1кН (значение на правой границе участка);

Q(3м) = –7,1кН+ 5кН/м·3м = 7,9кН (значение на левой границе участка);

Поскольку поперечная сила меняет знак в пределах участка, определяем координату, при которой она обращается в нуль:

Q(x₀) = –7,1кН+ 5кН/м ·x₀=0; x₀= 1, 42 м;

M (x₂) = – F(x₂+1м) + R_Bx₂– =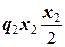

= – 7кН·(x₂+1м) + 14,1кН· x₂– 5кН/м· 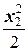= –7кНм +7,1кН·x₂–2,5кН/м· ;

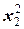Справа от сечения моменты всех сил, взяты относительно точки С₂(центр тяжести поперечного сечения – рис.13), положительное направление момента справа от сечения – против хода часовой стрелки.

Изгибающий момент (M) является квадратичной функцией координаты x₂.

Для построения его графика определяем значение изгибающего моментана границах участка и в найденной выше точке.

M (0) = –7кНм +7,1кН·0–2,5кН/м·0²= –7кНм (значение на правой границе);

M (1,42м) = –7кНм +7,1кН·1,42м–2,5кН/м·(1,42м) ² = –1,959 кНм = –1,96 кНм;

M (3м) = –7кНм +7,1кН·3м–2,5кН/м· (3м) ² = –8, 2 кНм (значение на левой границе участка).

Проводим сечение на III участке и рассматриваем правую от сечения часть балки (рис.13).

III участок 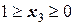(начало отсчета на правой границе участка);

Q(x₃) = F = 7кН;

Поперечная сила является постоянной, графиком такой функции служит прямая, параллельная осиx.

M(x₃) = – Fx₃ = –7кНм· x₃

Справа от сечения моменты всех сил, взяты относительно точки С₃(центр тяжести поперечного сечения – рис.13), положительное направление момента справа от сечения – против хода часовой стрелки.

M (0) = –7кНм·0 = 0 (значение на правой границе участка);

M (1м) = –7кН·1м= –7 кНм (значение на левой границе участка).