ЛАБОРАТОРНАЯ РАБОТА №5 ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЕЙ N-ГО ПОРЯДКА
Определителем n-го порядка, или определителем квадратной матрицы А=(aij) при n>1, называется число, полученное из элементов этой матрицы по формулам
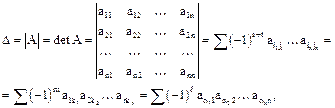
где s – число инверсий в верхней, а t – число инверсий в нижней строке подстановки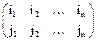 
и первая сумма берется по всем подстановкам; вторая сумма берется по всем перестановкам: (k1, …, kn) и m - число инверсий в этих перестановках. Аналогичный смысл имеет третья сумма. Слагаемые этих сумм являются членами определителя, количество всех слагаемых в каждой сумме равно n!
Рассмотрим некоторые способы вычисления определителей порядка n.
1. Вычисление определителя n-го порядка можно свести к вычислению определителя порядка n-1. Действительно, используя свойства определителя, можно все элементы какой-либо строки, кроме одного, сделать нулями, а затем разложить определитель по указанной строке, например, в определителе
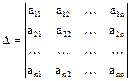
первый столбец умножаем на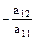 
и прибавляем ко второму, далее первый столбец, умноженный на 
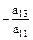, прибавляем к третьему и т.д. Получаем определитель вида
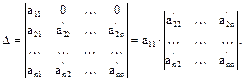
Общего метода вычисления определителей порядка n не существует, если не считать вычисление определителя заданного порядка непосредственно по его определителю. К определителю того или иного специального вида применяются различные методы вычисления, приводящие к более простым определителям.
2. Приведем к треугольному виду. Пользуясь свойствами определителя, приводим его к так называемому треугольному виду, когда все элементы, стоящие по одну сторону от главной диагонали равны нулю. Полученный определитель треугольного вида равен произведению элементов, стоящих на главной диагонали. Если удобнее получить нули по одну сторону от побочной диагонали, то он будет равен произведению элементов побочной диагонали, взятому со знаком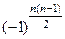 
. Действительно, произведение а1n, а2n-1…an1 является членом определителя и его знак определяет (-1)s, где s – число инверсий в перестановке (n, n-1, n-2,…, 2, 1). Следовательно, s=n-1+n-2+…+1= 
.
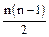Пример 1. Вычислить определитель n-ого порядка
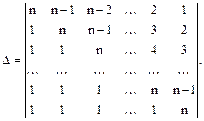
Вычтем из первой строки вторую, из второй – третью и т.д., наконец, из предпоследней последнюю (последняя строка остается без изменений).
Получим
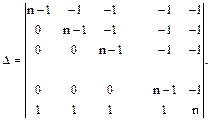
Элементы последней строки представим в виде сумм двух слагаемых 0+1, 0+1, …, 0+1, (n-1)+1. Применив свойство (аддитивности), будем иметь
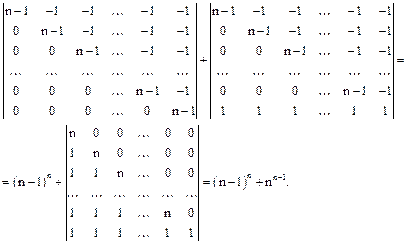
3. Вычисление определителя с помощью теоремы Лапласа. Если в определителе выделить k строк (или столбцов) (1£k£n-1), то определитель равен сумме произведений всех миноров k-ого порядка, расположенных в выделенных k строках (или столбцах), на их алгебрические дополнения.
Пример 2. Вычислить определитель
.
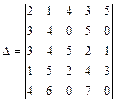В определителе десять миноров второго порядка, расположенных во второй и пятой строках, но только три из них отличны от нуля. Разложим определитель по второй и пятой строкам:
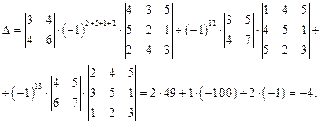
ВАРИАНТЫ ЛАБОРАТОРНОЙ РАБОТЫ
Вычислить определители
Вариант 1
; ; .
Вариант 2
; 
; 
.
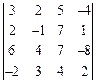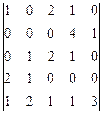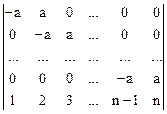Вариант 3
; 
; 
.
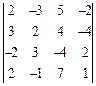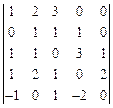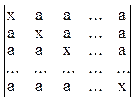Вариант 4
; 
; 
.
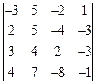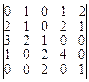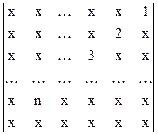Вариант 5
.
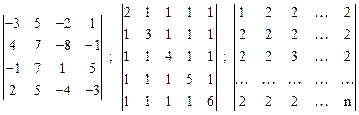Вариант 6
.
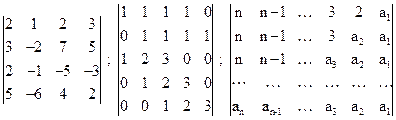Вариант 7
.
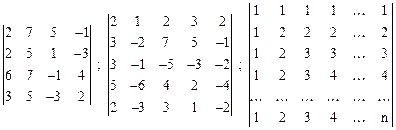Вариант 8
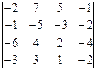
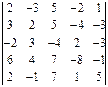
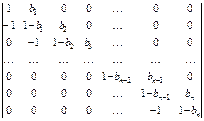
Вариант 9
.
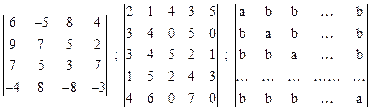Вариант 10
.
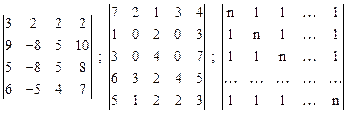Вариант 11
.
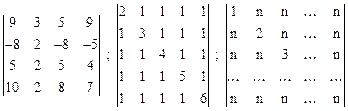Вариант 12
.
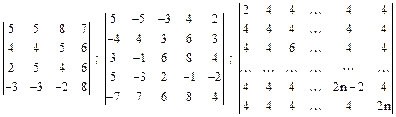Вариант 13
.
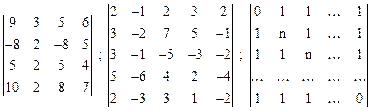Вариант 14
.