ЗАНЯТИЕ 2. Уравнения первого порядка с разделяющимися переменными. Систематизация и закрепление знаний.

☺ ☻ ☺

Замечание: При выполнении Задания необходимо руководствоваться основными понятиями, представленными в начале Занятия 1.

••• ≡•••

Пример 1–3: Показать, что при любом действительном значении параметра 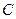заданная функция 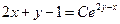является решением ДУ: 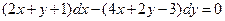. (1)

Решение:

1). Разделим уравнение (1) на 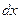: 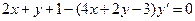. (2)

2). При нахождении производной заданной функции учтем, что функция 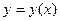в нашем примере задана неявно. Дифференцируем заданную функцию по x; учитывая :

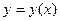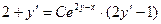=[учтём, что 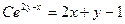]= 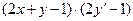. (3)

Применяя тождественные преобразования (3), получим: 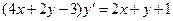. (4)

3). Подставив в уравнение (2) левую часть равенства (4), получаем очевидное тождество:

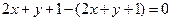
4). Это значит, что заданная (неявная) функция 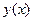является решением уравнения (1).

Ответ: заданная функция является решением заданного уравнения.

Пример 2–6: В заданном семействе 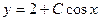выделить уравнение кривой, удовлетворяющей приведенному начальному условию: 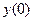= –1.

Решение:

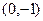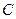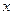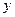1). Выделить из семейства кривых кривую, которая проходит через точку – это значит вычислить значение , при условии, что =0, = –1.

2). Подставим 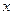=0, 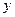= –1 в выражение семейства: 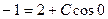, откуда 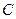= –3.

3). Тогда уравнение кривой семейства, проходящей через точку (0,1): .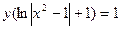

3). Запишем выражение кривой семейства, проходящей через точку : .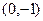

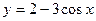Ответ: уравнение кривой: .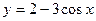

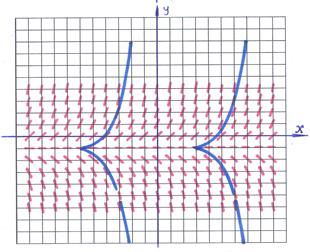
Пример 3–17: Методом изоклин построить приближенно семейство интегральных кривых для дифференциального уравнения: .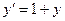

Решение:

1). Уравнение изоклин для заданного дифференциального уравнения получается из исходного уравнения приравниванием 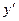= 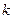. У нас каждая изоклина – прямая: 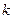= 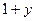. На рисунке изоклины выделены «серым» цветом: прямые, параллельные оси ОХ. На каждой изоклине черточка («красная») отражает конкретное значение 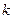, определяющее изоклину, то есть: на каждой изоклине наклон черточки один и тот же.

2). Черточки играют роль «железных опилок» в опытах по физике: они показывают направление «поля». Возникает «зрительный образ», который определяет «присутствие некоторой кривой», касательные к которой мы и видим. Это и есть приближенно выделяемая «интегральная кривая» (одна из них выделена «синим» цветом), то есть «решение» заданного ДУ.

Ответ: интегральная кривая представлена на рисунке.

Пример 4–23: Решить дифференциальное уравнение: .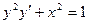

Решение:

1). Умножив исходное уравнение на дифференциал 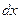, можем записать: 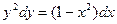. Нетрудно заметить, что это уравнение с разделяющимися переменными.

2). Отметим, что из исходной записи уравнения ни одного решения не следует.

3). Интегрируем уравнение: 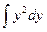= 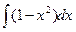. Используя табличные интегралы, нетрудно записать общее решение в виде: 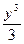= x– 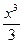+C, или в виде: .

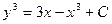Ответ: 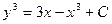– общее решение ДУ.

Пример 5–25: Решить дифференциальное уравнение: 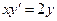. (1)

Решение:

1). Прежде всего, отметим, что исходное уравнение (1) имеет очевидное решение 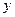=0.

2). Умножим исходное уравнение (1) на дифференциал 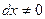. Уравнение (1) перепишем в дифференциальной форме: 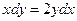. (2)

3). Нетрудно заметить, что уравнение (2) есть уравнение с разделяющимися переменными. Так как решение 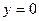уже учтено, теперь примем, что 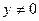и перепишем уравнение (2):

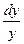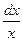=2 . (3)

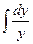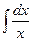4). Интегрируем (3): =2 или 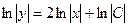→ 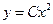. – общее решение дифференциального уравнения.

Ответ: общее решение ДУ 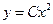; хотя при получении общего решения произвольная постоянная величина 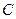не должна принимать значение 0, формально из него можно получить решение исходного уравнения 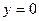при значении .

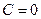Пример 6–30: Решить дифференциальное уравнение: 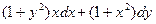. (1)

Решение:

1). Прежде всего, отметим, что исходное уравнение (1) не предлагает простейших решений вида: 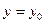и .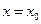

2). Запишем уравнение (1) в виде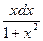: 2 +2 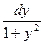=0. Умножение на число 2 учитывает, что !

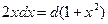3). В результате интегрирования получим: 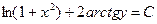– общее решение ДУ.

Ответ: общее решение ДУ: .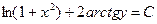

Пример 7–38: Решить дифференциальное уравнение: 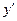= 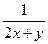. (1)

Решение:

1). Прежде всего, отметим, что исходное уравнение (1) не предлагает простейших решений вида: 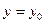и 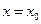. Также легко заметить, что уравнение (1) равносильно уравнению:

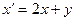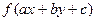= . (2)

2). Примем 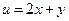и вычислим производную 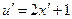, то есть 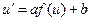. В нашем случае получаем 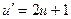, что есть уравнение с разделяющимися переменными!

3). Уравнение 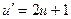имеет решение в виде функции: 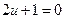. Учитывая обозначение 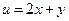, запишем решение 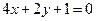– прямая линия.

Замечание: Увидеть решение 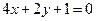непосредственно из исходного уравнения было бы совсем непросто!

4). Пусть теперь 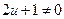. Запишем уравнение 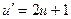в виде: 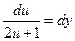, или (для удобства!) в виде: 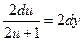. (3)

5). Интегрирование уравнения (3) не составит труда, даже на начальном этапе освоения неопределённого интеграла 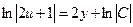→ 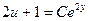. (4)

Ответ: общее решение ДУ 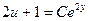; в данном случае решение 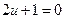можно получить формально из общего при значении 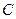=0; запишем общее решение и в виде 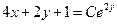, из которого решение 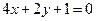получается из общего при значении 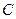=0.

☻

Вопросы для самопроверки:

1. Какое уравнение называют дифференциальным?

2. Как определить порядок ДУ?

3. Что такое решение ДУ, частное решение ДУ?

4. Что такое общее решение ДУ?

5. Что значит решить Задачу Коши?

6. Что такое семейство кривых?

7. Как построить уравнение, решением которого является заданное семейство кривых?

8. Каковы стандартные формы ДУ с разделяющимися переменными?

9. Какова стандартная схема решения ДУ с разделяющимися переменными?

Задачи для самоподготовки:

Пример C2–1: Показать, что при любом действительном значении параметра 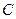заданная функция 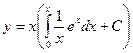является решением ДУ: .

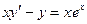Ответ:заданная функция является решением ДУ.

Пример C2–2: Составить дифференциальное уравнение семейства гипербол: .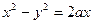

Ответ: .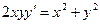

Пример C2–3: Методом изоклин построить приближенно семейство интегральных кривых для дифференциального уравнения: y′= – .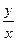

Ответ:рисунок семейства прилагается.

Пример C2–4: Решить дифференциальное уравнение: y′ = .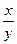

Ответ:x² – y² = C – общее решение ДУ (семейство гипербол).

Пример C2–5: Решить дифференциальное уравнение: y′ + 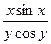= 0.

Ответ: 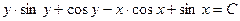– общее решение ДУ.

Пример C2–6: Найти частное решение ДУ: 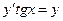, удовлетворяющее условию: 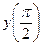=1.

Ответ: 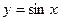– частное решение ДУ. Через точку 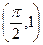проходит единственная кривая.

< * * * * * >

• •••☻••• •

Разработчик: к. т. н., доцент кафедры ВМ-2 ____________________ (А. И. Литвинов)