Дифференциальные уравнения
Дифференциальным уравнением называется уравнение, связывающее между собой независимую переменную х, искомую функцию у и её производные или дифференциалы.
Символически дифференциальное уравнение записывается так:
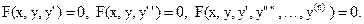
Дифференциальное уравнение называется обыкновенным, если искомая функция зависит от одного независимого переменного.
Порядком дифференциального уравнения называется порядок старшей производной (или дифференциала), входящей в данное уравнение.
Решением (или интегралом) дифференциального уравнения называется такая функция, которая обращает это уравнение в тождество.
Общим решением (или общим интегралом) дифференциального уравнения называется такое решение, в которое входит столько независимых произвольных постоянных, каков порядок уравнения. Так, общее решение дифференциального уравнения первого порядка содержит одну произвольную постоянную.
Частным решением дифференциального уравнения называется решение, полученное из общего при различных числовых значениях произвольных постоянных. Значения произвольных постоянных находятся при определённых начальных значениях аргумента и функции.
Дифференциальным уравнением первого порядка называется уравнение, в которое входят производные (или дифференциалы) не выше первого порядка.
Дифференциальным уравнением с разделяющимися переменными называется уравнение вида:
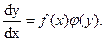
Для решения этого уравнения нужно сначала разделить переменные:
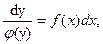
а затем проинтегрировать обе части полученного равенства:
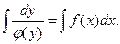
1.Найти общее решение уравнения 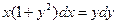
Разделив переменные, имеем:
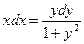
Интегрируя обе части полученного уравнения:
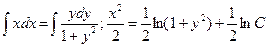
Так как произвольная постоянная С может принимать любые числовые значения, то для удобства дальнейших преобразований вместо С мы написали (1/2)lnC. Потенцируя последнее равенство, получим:
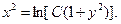 ·
·
Это и есть общее решение данного уравнения.
2.Найти частное решение уравнения 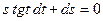 ,удовлетворяющее начальным условиям
,удовлетворяющее начальным условиям 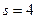 при
при 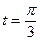 .
.
Разделив переменные, имеем:
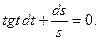
Проинтегрируем обе части полученного уравнения:
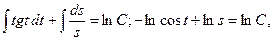
или
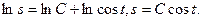
Это общее решение данного уравнения .Для нахождения значения произвольной постоянной С подставим значения 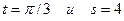 в выражение для общего решения:
в выражение для общего решения: 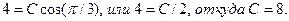
Следовательно, искомое частное решение, удовлетворяющее указанным начальным условиям, имеет вид 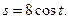 ·
·
Элементы комбинаторики и теории вероятностей.
Элементы комбинаторики.
Группы, составленные из каких-либо элементов, называются соединениями.
Различают три основных вида соединений: размещения, перестановки и сочетания.
Задачи, в которых производится подсчет возможных различий соединений, составленных из конечного числа элементов по некоторому правилу, называются комбинаторными. Раздел математики, занимающийся их решением, называется комбинаторикой.
- Размещения. Размещениями из n элементов по m в каждом называются такие соединения, которые отличаются друг от друга либо самими элементами (хотя бы одним), либо порядком их расположения.
Число размещений из n элементов по m обозначается символом 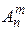 и вычисляют по формуле:
и вычисляют по формуле:
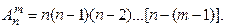 (1.33)
(1.33)
- Перестановки. Перестановками из n элементов называются такие соединения из всех n элементов, отличаются друг от друга порядком расположения элементов. Число перестановок из n элементов обозначается символом
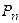 .
.
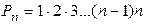 (1.34)
(1.34)
Число всех перестановок из n элементов равно произведению последовательных чисел от 1 до n включительно. Произведение 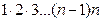 обозначается символом n! (читается «n – факториал»), причем полагают 0!=1, 1!=1. Поэтому равенство (1.34) можно переписать в виде:
обозначается символом n! (читается «n – факториал»), причем полагают 0!=1, 1!=1. Поэтому равенство (1.34) можно переписать в виде:
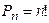 (1.35)
(1.35)
Используя формулу (1.35), формуле (1.33) можно придать вид:
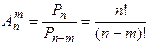
- Сочетания. Сочетаниями из n элементов по m в каждом называются такие соединения, которые отличаются друг от друга хотя бы одним элементом.
Число сочетаний из n элементов по m обозначается 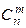 . Оно находится по формуле:
. Оно находится по формуле:
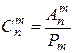 (1.36)
(1.36)
Которую можно записать также в виде:
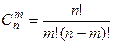 (1.37)
(1.37)
Кроме того, при решении задач используются следующие формулы, выражающие основные свойства сочетаний:
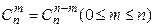 (1.38)
(1.38)
(по определению полагают 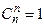 и
и 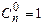 )
)
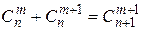 (1.39)
(1.39)
1.Найти число размещений: 1) из 10 элементов по 4; 2) из n+4 элементов по n-2.
Согласно формуле (1.33), получим:
1) 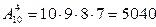 ;·
;·
2) 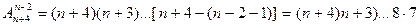 ·
·
2.Решить уравнение 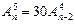
Используя формулу (1.33), перепишем уравнение в виде 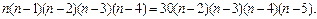
Учитывая, что 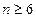 , разделим обе его части на
, разделим обе его части на 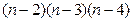 ; далее, имеем
; далее, имеем
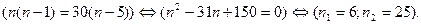 ·
·
3.Составить всевозможные перестановки из элементов 1) 1; 2) 5,6; 3) a,b,c.
(1); 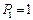 ; 2) (5,6); (6,5);
; 2) (5,6); (6,5); 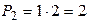 ; 3) (a,b,c); (a,c,b); (b,c,a); (b,a,c); (c,b,a); (c,a,b);
; 3) (a,b,c); (a,c,b); (b,c,a); (b,a,c); (c,b,a); (c,a,b); 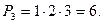 ·
·
4.Вычислить значения выражений: 1) 5!+6!; 2) 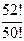 .
.
1) 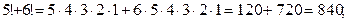 ·
·
2) 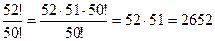 ·
·
5.Вычислить: 1) 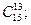 2)
2) 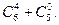
· Согласно формуле (1.37), получим:
1) 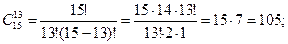 ·
·
2) 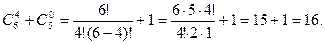 ·
·
