Вычисление определенного интеграла

Все методы интегрирования, используемые при нахождении неопределенных интегралов, применяются и при вычислении определенных интегралов.

Непосредственное интегрирование.

Пример 1. Вычислить интеграл

а)

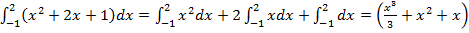
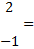
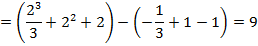
b)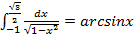

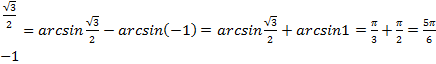
2. Метод подстановки (замена переменной) для определенного интеграла состоит в следующем:

1) часть подынтегральной функции заменить новой переменной;

2) найти дифференциал обеих частей замены;

3) найти новые пределы интегрирования;

4) все подынтегральные выражения выразить через новую переменную;

5) вычислить полученный интеграл.

Пример 2. Вычислить интеграл методом замены переменной

а)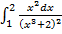

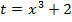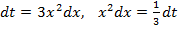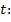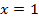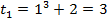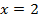Решение: Положим , тогда . Определим пределы интегрирования для новой переменной при получаем при получаем 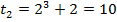. Вычислим получившийся интеграл:

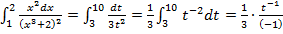
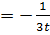
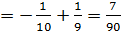
Приложения определенного интеграла

а) Вычисление площадей плоских фигур

Определение:Криволинейной трапецией называется фигура, ограниченная графиком непрерывной неотрицательной функции 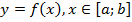, прямыми 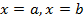и отрезком оси .

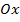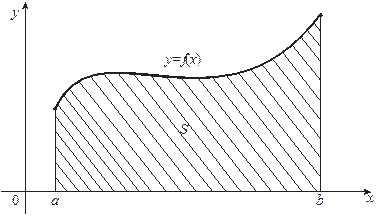
1) Пусть 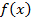непрерывная неотрицательная функция на отрезке 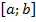, тогда ее график расположен над осью 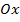. Если фигура, расположенная над осью 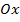является криволинейной трапецией, то ее площадь вычисляется по формуле:

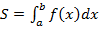(1)

2) Пусть 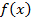непрерывная неположительная функция на отрезке 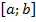, тогда ее график расположен под осью 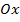. Если фигура, расположенная под осью 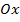является криволинейной трапецией, то ее площадь вычисляется по формуле:

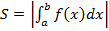(2)

3) Пусть фигура ограничена двумя пересекающимися кривым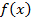и и 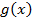и прямыми 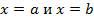, где и 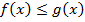. Тогда ее площадь вычисляется по формуле:

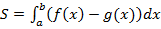(3)

б) Вычисление объемов тел вращения

Объем тела, образованного вращением вокруг оси 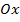криволинейной трапеции, ограниченной непрерывной кривой 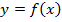, где 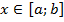, прямыми 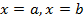и отрезком оси 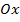вычисляется по формуле:

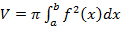(4)

Примеры решения задач

Пример 1. Вычислить площадь фигуры, ограниченной линиям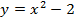и:

и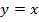

Решение:Построим параболу 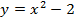и прямую 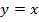в одной координатной плоскости

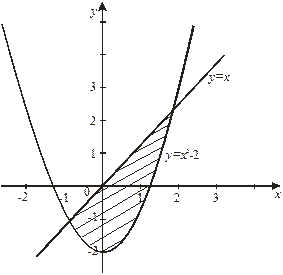
Для определения абсцисс точек пересечения решим уравнение: 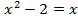. Получаем 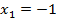и 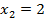. Следовательно, 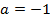и 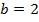. На отрезке 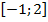имеем: 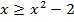. Значит для нахождения искомой площади воспользуемся формулой (3):

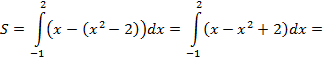
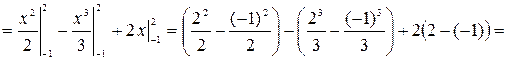
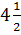(кв. ед.).

Ответ: 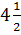(кв. ед.).

Пример 2. Найти объем тела, полученного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями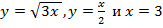

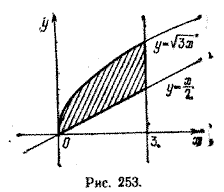Решение: Очевидно, что объем данного тела вращения равен разности объемов тел, полученных вращением криволинейных трапеций, соответствующих функциям 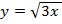и , .

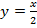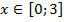Обозначим эти объемы через 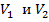. Найдем их по формуле (4):

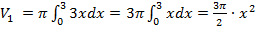
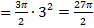
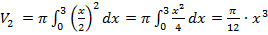
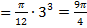
Искомый объем равен: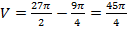

Ответ: 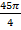(куб. ед.)