Если функция непрерывна на отрезке достигает
A.наибольшего и наименьшего значения B. наибольшего значения
C.наименьшего значения
D. постоянна.
3.продолжите фразу:
если функция непрерывна на отрезке 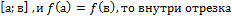
A.возрастает
B. 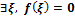
C.ограничена
D.постоянна.
4.запишите формулу углового коэффициента касательной :
A. 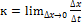 B.
B. 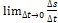
C. 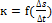 D. Это тангенс
D. Это тангенс
5.уравнение касательной к графику в т х0
A. y= 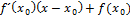
B. y= 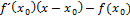
C. y= 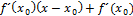
D. y= 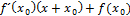
6.запишите формулу скорости материальной точки в момент времени 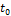 :
:
A. 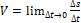 B .
B . 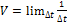
C. . 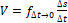 D. .
D. . 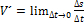
7.как называется процесс вычисления производной:
А.интегрирование В.логарифмирование
С.дифференцирование D.сложение
8.запишите формулу физического смысла производной:
А.f´(х)=а В.f´(х)=х-а
С.f´(х)=-х D. 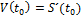
9. запишите формулу экономического смысла производной:
А.f´(х)=а В.f´(х)=х-а
С.Z´=U´(t0) D. 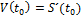
10.необходимым , но недостаточным условием дифференцируемости функции является:
А.четность В.нечетность
С.непрерывность D.возрастание
11.функция называется гладкой, если
А.сплошная линия В.непрерывна её f´(х)
С.она непрерывна D .положительна
12. функция называется кусочно -гладкой, если:
А.сплошная линия В.непрерывна её f´(х)
С. 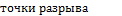 D.положительна
D.положительна
13.если в тх0 не существует предела конечного или бесконечного, то геометрически это-
А.отсутствие функции В.производная
С.отсутствие касательной D.нуль функции
14.производная обратной функции равна:
А.обратной величине производной заданной функции
В. Производной обратной функции
С.производной заданной функции в (-1) степени
D.самой функции, без изменений.
15.производная второго порядка это-
А.производная от производной первого порядка
В.производная во второй степени
С.сама производная , без функции
D. несколько производных сразу.
16.механический смысл второй производной:
А. 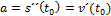 B. a=v2
B. a=v2
C.f=a-v(t) D.a=v´´
17.запишите формулу правила Лопиталя:
А. 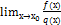
В. 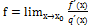
С. 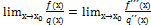
D. 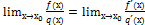
18.что позволяет сравнивать правило Лопиталя?
А.бесконечные формулы
В.бесконечно большие величины
С.бесконечности
D.переменные.
19.какие виды неопределенностей рассматривает правило Лопиталя?
А. 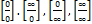 В. А.
В. А. 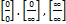
С. А. 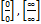 D. А.
D. А. 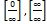
20.перечислите виды производственных издержек:
А. общие, частные
В.квартальные
С.годовые
D.постоянные, удельные, маржинальные
Тест по предмету завершен.
Дата заполнения_____________________
Экзаменационное тестовое задание
по предмету «математика для экономистов»,
2 курс
Вариант № 10
Ф.И. студента_____________________
группа_______________
1.запишите формулу эластичности функции:
А. 
С. 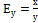 D.
D. 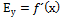
2.перечислите теории потребления:
А.кординальная В.прямолинейная
С.криволинейная ,функциональная
D.кардиналистская, ординалистская
3.назовите виды коэффициентов эластичности:
А.прямой, перекрестный В.линейный
С.не линейный D.монопольный.
4.назовите виды рынков:
А.совершенной конкуренции, монопольный
В.рыночный
С.хаотический
D.средний, высший, низший
5.основная характеристика монопольного рынка:
А.средний и предельный доход совпадают
В.с ростом реализованной продукции предельный доход падает
С.выручка всегда растет
D. предельный доход растет
6.назовите основную характеристику рынка совершенной конкуренции:
А.средний и предельный доход совпадают
В.с ростом реализованной продукции предельный доход падает
С.выручка всегда растет
D. предельный доход растет
7.запишите формулу геометрического смысла эластичности:
А. 
С. 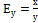 D.
D. 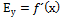
8.запишите формулу темпа изменения функции:
А. 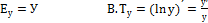
С. 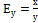 D.
D. 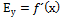
9.свойство эластичности суммы функций:
А. 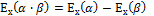
В. 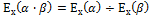
С. 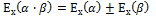
D. 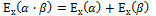
10.свойство эластичности частного:
А. 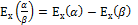
В. 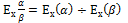
С. 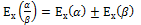
D. 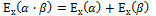
11.формула эластичности взаимно –обратных:
А. 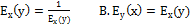
В. 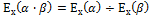
С. 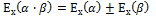
D. 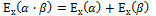
12.некоторая прямая, к которой данная прямая неограниченно приближается – это:
А.хорда В.диаметр
С.медиана D.асимптота.
13.виды асимптот:
А.касательная В.линейная
С.горизонтальная
D.горизонтальная, вертикальная, наклонная.
14.условие существования вертикальной асимптоты:
А.не пересекаться с графиком
В. 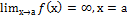
С. 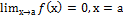
D. 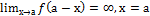
15. условие существования горизонтальной асимптоты:
А.не пересекаться с графиком
В. 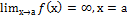
С. 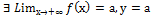
D. 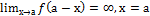
16. условие существования наклонной асимптоты: у=кх+в
А. 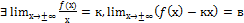
В. 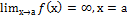
С. 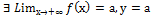
D. 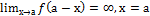
17.сколько наклонных асимптот может иметь функция:
А.5 и более В.не более двух
С.одну D.сколь угодно много
18.горизонтальная асимптота является частным случаем :
А.наклонной В.вертикальной
С.горизонтальной D.всех сразу.
19.укажите правильную формулу: 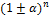
А. 
С. 
20. укажите правильную формулу: 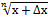
А. 
С. 
Тест по предмету завершен .
Дата заполнения_______________________.
Экзаменационное тестовое задание
по предмету «математика для экономистов»,
2 курс
Вариант № 11
Ф.И. студента_____________________
группа_______________
1.укажите правильную формулу: 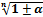
А. 
С. 
2.укажите правильную формулу:
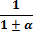
А. 
С. 
3. укажите правильную формулу:
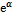
А. 
С. 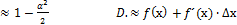
4.укажите правильную формулу:
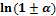
А. 
С. 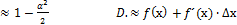
5. укажите правильную формулу:

А. 
С. 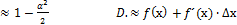
6. укажите правильную формулу:
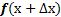
А. 
С. 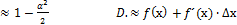
7.функция это –
А.взаимное соответствие
В.однозначное соответствие
С. связь между х и у
D.взаимно – однозначное соответствие.
