Раздел 1. Дифференциальные уравнения первого порядка
СПИСОК вопросов к модулю 1 По курсу
«Дифференциальные уравнения»
Осенний семестр, 2-й курс
Модуль 1. Дифференциальные уравнения (ДУ)
Раздел 1. Дифференциальные уравнения первого порядка
1. Какие практические задачи приводят к ДУ?
2. Что является предметом изучения в теории ДУ?
3. Какие ученые являются основоположниками теории ДУ?
4. С какими прикладными науками связана теория ДУ?
5. Все ли ДУ допускают аналитическое решение?
6. Дать определение ДУ.
7. Какое ДУ называется обыкновенным?
8. Дать определение уравнения в частных производных.
9. Как определяется порядок ДУ?
10.Дать определение решения ДУ.
11.Что понимают под интегрированием ДУ?
12.Запишите обыкновенное ДУ 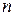 -го порядка в общем виде и раскройте смысл всех входящих в ДУ величин.
-го порядка в общем виде и раскройте смысл всех входящих в ДУ величин.
13.Дать определение интегральной кривой ДУ.
14.Записать ДУ первого порядка в общем виде и раскрыть смысл всех входящих в уравнение величин.
15.Записать ДУ первого порядка, разрешенное относительно производной.
16.Привести простейший пример ДУ первого порядка, разрешенного относительно производной, и представить решение такого ДУ.
17.Объяснить назначение начального условия ДУ.
18.Раскрыть геометрический смысл начального условия.
19.Дать определение ДУ с разделяющимися переменными.
20.Объяснить принцип решения дифференциального уравнения с разделяющимися переменными.
21.Привести дифференциальную форму ДУ с разделяющимися переменными.
22.Показать, как от дифференциальной формы ДУ с разделяющимися переменными перейти к исходной форме.
23.Привести пример ДУ, приводящегося к ДУ с разделяющимися переменными.
24.Дать определение общего решения ДУ первого порядка.
25.Дать определение частного решения ДУ.
26.Объяснить принцип определения частного решения ДУ по его общему решению.
27.Объяснить геометрический смысл общего и частного решений ДУ первого порядка.
28.Дать определение однородной функции.
29.Дать определение однородного ДУ.
30.Какая замена переменных используется при решении однородного ДУ?
31.Объяснить принцип решения однородного ДУ.
32.Записать ДУ, приводящееся к однородному ДУ.
33.Какая замена переменных используется при приведении ДУ к однородному ДУ?
34.Объяснить принцип приведения ДУ к однородному ДУ.
35.Записать общий вид ДУ, приводящегося к однородному ДУ.
36.Дать определение линейного ДУ первого порядка.
37.Какое уравнение называется однородным линейным ДУ?
38.Какое уравнение называется неоднородным линейным ДУ?
39.Объяснить метод решения линейного ДУ первого порядка.
40.Дать определение ДУ Бернулли.
41.Объяснить принцип решения ДУ Бернулли.
42.К какому типу ДУ сводится решение ДУ Бернулли?
43.Сформулировать условие Липшица для функции одной переменной.
44.Привести достаточное условие для выполнения условия Липшица.
45.Сформулировать теорему Коши для ДУ первого порядка.
46.Дать определение задачи Коши для ДУ первого порядка.
47.Привести пример ДУ первого порядка, удовлетворяющего условиям теоремы Коши.
48.Теорема Коши дает необходимые или достаточные условия существования и единственности решения ДУ первого порядка?
49.Какова роль требования выполнения условия Липшица в теореме Коши?
50.Сформулировать теорему о существовании решения ДУ без выполнения условия Липшица.
51.Дать определение особой точки ДУ первого порядка.
52.Чем обусловлено наличие особых точек ДУ первого порядка?
53.Дать определение особого решения ДУ первого порядка.
54.Чем отличается особое решение ДУ первого порядка от его частного решения?
55.Как составить ДУ первого порядка по его общему решению?
56.Как построить ДУ однопараметрического семейства кривых?
57.Дать определение ортогональных траекторий семейства кривых.
58.Как построить ДУ ортогональных траекторий семейства кривых?
59.Как получить алгебраическое уравнение ортогональных траекторий семейства кривых?
60.Запишите общий вид ДУ первого порядка, не разрешенного относительно производной.
61.Приведите общий вид ДУ первого порядка, которое не содержит аргумента и функции.
62.Дайте метод решения ДУ первого порядка, которое не содержит аргумента и функции.
63.В какой форме представляется общее решение ДУ первого порядка, которое не содержит аргумента и функции?
64.Приведите общий вид ДУ первого порядка, которое не содержит аргумента и разрешимо относительно функции.
65.Дайте метод решения ДУ первого порядка, которое не содержит аргумента и разрешимо относительно функции.
66.В какой форме представляется общее решение ДУ первого порядка, которое не содержит аргумента и разрешимо относительно функции?
67.Запишите общий вид ДУ первого порядка, которое не содержит функции и разрешимо относительно аргумента.
68.Приведите метод решения ДУ первого порядка, которое не содержит функции и разрешимо относительно аргумента.
69.В какой форме представляется общее решение ДУ первого порядка, которое не содержит функции и разрешимо относительно аргумента?
70.Дать определение ДУ Клеро.
71.Объяснить принцип решения ДУ Клеро.
72.В какой форме представляется общее решение ДУ Клеро?
73.Как найти общее решение ДУ Клеро?
74.Что представляет собой геометрически общее решение ДУ Клеро?
75.Как найти особое решение ДУ Клеро?
76.Что представляет собой геометрически особое решение ДУ Клеро?
77.Дать определение ДУ Лагранжа.
78.Чем отличается ДУ Клеро от ДУ Лагранжа?
79.К какому типу ДУ сводится решение уравнения Лагранжа?
80.Перечислите все изученные типы ДУ первого порядка, допускающие интегрирование в квадратурах.
