Остроение структуры системы управления, программная реализация регуляторов.

екция 5

Большинство систем процессорного (компьютерного) управления содержат в своем составе различные регуляторы, выполненные программным образом либо реализованные аппаратно. В настоящее время на практике используются как аналоговые, так и цифровые регуляторы.Регуляторы можно строить на основе как аналоговой, так и цифровой модели. Соответственно, для анализа и проектирования аналогового и цифрового регулятора требуются разные математические методы. Хотя цифровая технология позволяет хорошо моделировать работу аналоговой системы управления, т.е. реализовать готовые физические модели цифровыми средствами, ее возможности гораздо шире. Например, можно построить нелинейные и самонастраивающиеся регуляторы, которые не возможно создать на основе только аналоговых средств. Главная задача при цифровом управлении ‑ найти соответствующую структуру регулятора и его параметры. После определения этих параметров реализация алгоритмов управления обычно представляет собой не сложную задачу. Помимо этого, каждый регулятор должен обеспечивать защитные функции, предотвращающие опасное развитие процесса в нештатных ситуациях.

Проектирование регуляторов.

Регулятор в составе цифровой системы управления по определению является дискретным. Однако большинство динамических систем описываются обыкновенными дифференциальными уравнениями. Аналоговый регулятор можно спроектировать на основе описания непрерывной системы с помощью передаточной функции или в пространстве состояний. Для того чтобы аналоговый регулятор реализовать компьютерными средствами, его модель необходимо подвергнуть процедуре квантования. При цифровом управлении можно идти другим путем, а именно ‑ использовать в качестве исходной дискретную динамическую модель процесса, а затем спроектировать регулятор непосредственно по этой модели.

Если регулятор сначала проектируется как аналоговый, а затем преобразуется в дискретную форму, то интервал выборки обычно меньше, чем в случае, если он спроектирован на основе дискретной модели. Это означает более высокую загрузку управляющего процессора, что может затруднить или сделать невозможным построение системы управления с требуемыми характеристиками.

С некоторыми допущениями можно считать, что все линейные регуляторы с одним входом и одним выходом можно представить в обобщенном виде

u(k·h)=-r₁·u[(k-1)·h]-…-r_n·u[(k-n)·h]+

+t₀·u_з(k·h)+t₁·u_з[(k-1)·h]+ … +t_n·u_з[(k-n)·h]- (1.31)

-s₀·y(k·h)-s₁·y[(k-1)·h]-… -s_n·y[(k-n)·h]

где u ‑ это выход регулятора (управляющая переменная физического процесса, u_з ‑ опорное (задающее) значение, у ‑ выходной сигнал (управляемая переменная) физического процесса. Параметр n представляет собой порядок регулятора. Обычно регулятор может рассматриваться как частный случай обобщенного дискретного регулятора при n=2. Хотя большинство процессов в действительности нелинейны, тем не менее, с помощью линейных регуляторов возможно успешно управлять значительной частью таких систем.

Простейшие регуляторы реализуют коррекцию управлений по рассогласованию между заданным и реальным значениями управляемого параметрами. Такое рассогласование может быть обусловлено с одной стороны – изменением задающего воздействия, с другой стороны – внешними возмущениями. В первом случае имеет место "известное" возмущение. Можно построить регулятор, который будет использовать соответствующую информацию для упреждающего управления (feedforward control).

В структуре такого регулятора два контура (рис. 1.5)

Рис. 1.7. Структура регулятора с упреждением.

Контур упреждающего управления контролирует изменение задающего сигнала и формирует корректирующую поправку к выходному сигналу управления для того, что бы система более оперативно, с минимальной погрешностью реагировала на входной сигнал.

Если возмущения, действующие на управляемую систему, имеют предсказуемое поведение и их можно измерить, то можно провести упреждающее управление до того, как выходной параметр изменится значительно. В этом случае регулятор обеспечивает упреждающее управление по возмущению (feedforward from process disturbances), которое в определенных случаях позволяет существенно улучшить качество управления. Эти способы упреждающего управления базируются на предположении относительно будущего поведения системы. Для этого упреждающие регуляторы должны включать в себя модель динамики управляемой технической системы.

Основные принципы разработки структур управления.

Качество упреждающего управления в значительной степени зависит от качества измерения возмущений и точности модели процесса. Любой реальный регулятор должен сочетать в себе упреждающее управление по опорному значению и возмущению с контуром обратной связи. Упреждающее воздействие обеспечивает быструю коррекцию ошибок выходного параметра процесса, обусловленных изменением опорного значения или возмущениями, а обратная связь ‑ более медленную реакцию на изменение выхода процесса.

Главное преимущество обратной связи в том, что она компенсирует неточности модели процесса, погрешности измерений и ошибки выходной величины, связанные с неучтенными возмущениями. Ниже перечислены основные положения, которые необходимо учитывать при создании систем с обратной связью и упреждающим управлением.

Ограничения управления с обратной связью, которые могут быть компенсированы упреждающим управлением:

· Механизм обратной связи не вносит коррективы до тех пор, пока не будет обнаружено отклонение в величине выходного параметра. Поэтому "идеальное" управление, при котором управляемая величина точно повторяет измерения опорного значения или некоторое время не влияет на изменение характеристик процесса, практически невозможно.

· Даже если возмущения известны, обратная связь не может их компенсировать предсказуемым образом.

· В системах с большими постоянными времени или с большими задержками обратная связь работает неудовлетворительно. При наличии больших и частых возмущений процесс может быть прекращен из-за того, что он постоянно носит переменный характер и никогда не достигает предусмотренного установившегося состояния.

· Если точное значение выходной переменной нельзя измерить, управление с обратной связью невозможно.

Причины, затрудняющие упреждающее управление:

· Для многих приложений невозможно постоянно в оперативном режиме измерять возмущения.

· Необходимо иметь адекватную модель физического процесса ‑ качество упреждающего управления зависит от точности модели процесса.

· Во многих случаях упреждающий регулятор должен выполнять точное дифференцирование, которое практически сложно реализовать.

· Структура регулятора должна включать в себя как упреждающее управление по задающему (опорному) значению и возмущениям процесса, так и обратную связь по выходной величине процесса.

Наибольшее практическое распространение получили ПИД – регуляторы (Proportional-Integral-Derivative). На его выходе формируется сигнал, определяемый тремя составляющими. Первая – пропорциональна ошибке выходной величины, вторая – обеспечивает интегральную зависимость от входного сигнала, третья – корректирует выходной сигнал в зависимости от скорости изменения задающего воздействия.

Классический ПИД-регулятор описывается следующим уравнением

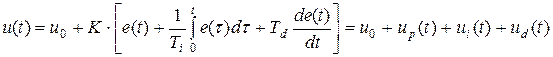(1.32)

где u₀ – начальное значение выхода регулятора (уставка), e(t) – ошибка выхода регулятора, K – коэффициент усиления регулятора, T_i – постоянная времени интегрирования, T_d – постоянная времени дифференцирования.

При реализации ПИД-регулятора на аналоговых микросхемах, изменения его параметров K, T_d, T_i производятся соответствующими подстроечными резисторами. Однако, изменение одного из них приводит к некоторому изменению настроек других – имеется взаимовлияние, обусловленное схемотехникой построения регулятора. При цифровом (программном) выполнению регулятора эти проблемы отсутствуют.

Существует два типа алгоритма регулятора ‑ позиционный и алгоритм приращений. В позиционном алгоритме (position form) выходной сигнал представляет собой абсолютное значение управляющей переменной исполнительного механизма. Дискретный ПИД-регулятор имеет вид

u(k∙h) =u₀ + u_p(k∙h) + u_i(k∙h) + u_d(k∙h) (1.33)

Даже при нулевой ошибке управления выходной сигнал отличен от нуля и определяется смещением u₀. В соответствии с уравнением (1.32) пропорциональная часть регулятора имеет вид

u_p(k∙h)=K∙e(k∙h) (1.34)

Интеграл аппроксимируется конечными разностями

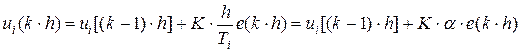(1.35)

с постоянной 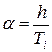(1.36)

величина второго слагаемого в уравнении (1.35) при малых h и больших T_i может стать очень малой, поэтому при алгоритмической реализации нужно позаботиться о том, чтобы обеспечить необходимую точность его машинного представления. Дифференциальная часть ПИД-регулятора

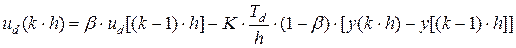(1.37)

где 0<β<1.

Альтернативным подходом является алгоритм ПИД-регулятора, в котором вычисляется лишь изменение его выходного сигнала. Алгоритм приращений (incremental form) ПИД-регулятора удобно применять, если исполнительный механизм представляет собой разновидность интегратора, например шаговый двигатель, либо устройство сохраняющее свое состояние до следующего управления. В алгоритме приращений рассматриваются только изменения управляющего выходного сигнала от момента времени (k-l)·h до момента k∙h. Алгоритм регулятора записывается в виде

Δu(k·h)=Δu_p(k∙h)+Δu_i(k·h)+Δu_d(k·h) (1.38)

Пропорциональная часть алгоритма приращений

Δu_p(k∙h)=u_p(k∙h)-u_p[(k-1)·h]=K∙[e(k∙h)-e[(k-1)∙h]=K∙Δe(k∙h) (1.39)

интегральная часть

Δu_i(k∙h)=u_i(k∙h)-u_i[(k-1)·h]=K∙α∙e(k∙h) (1.40)

дифференциальная часть регулятора

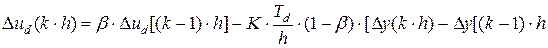(1.41)

где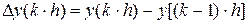

С вычислительной точки зрения алгоритм несложен. Для его применения, как правило, достаточно операций с плавающей точкой одинарной точности. В алгоритме не возникает проблем из-за насыщения регулятора. Небольшим недостатком алгоритма приращений является необходимость учитывать интегральную составляющую. Опорное значение сокращается как в пропорциональной, так и дифференциальной частях, начиная со второй выборки после его изменения. Поэтому, если используется регулятор на базе алгоритма приращений без интегральной составляющей, возможен дрейф управляемого процесса от опорного значения.

Определение частоты выборки сигналов датчиков в системах управления.

Ранее уже упоминались некоторые вопросы оцифровки аналоговых сигналов и определения необходимой частоты выборки. Определение адекватной частоты выборки для процесса управления представляет собой нетривиальную задачу. Слишком малая частота выборки может снижать эффективность управления, в особенности способность системы компенсировать возмущения. Однако если интервал выборки превосходит время реакции процесса, возмущение может повлиять на процесс и исчезнуть прежде, чем регулятор сформирует корректирующее воздействие. Поэтому при определении частоты выборки важно учитывать как динамику процесса, так и характеристики возмущения. С другой стороны, частота выборки не должна быть слишком высокой, так как это ведет к повышенной загрузке процессора. Стандартные цифровые регуляторы, работающие с небольшим числом контуров управления (от 8 до 16), используют фиксированную частоту выборки порядка долей секунды.

На определение частоты выборки также влияет соотношение сигнал/шум измерительного тракта. При его малых значениях, т.е. при больших шумах, следует избегать высокой частоты выборки, потому что отклонения в измерительном сигнале скорее связаны с высокочастотным шумом, а не с реальными изменениями в физическом процессе.