Разрешающие уравнения рассматриваемых задач

Задача растяжения панели. С учетом вида первоначально выбранных функций, а также и , в задаче растяжения равны нулю коэффициенты , а между остальными коэффициентами существует связь

; ; ; ; . (3.15)

Чтобы получить аналитическое решение задачи, оставим в ряду разложения функций перемещений по две первые 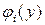и 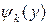, а для того чтобы начальную систему уравнений можно было решить в аналитическом виде и выделить уравнение растяжения, проведем такую ортогонализацию функци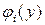й и 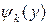, чтобы коэффициенты с индексами 12 и 21 стали равными нулю. Увеличение числа аппроксимирующих функций приводит к увеличению числа уравнений и решение системы можно реализовать только с помощью математических программ. Рассматривая выражения коэффициентов (3.15), можно заметить, что коэффициенты ; обратятся в нуль, если функция будет ортогональна с функциями и . В этом случае введем новую функцию , где и есть коэффициенты ортогонализации, которые определятся из условий

(3.16)

Здесь функции 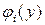можно представить как ; ; .

Коэффициенты ; ; будут равны нулю, если ввести новую функцию , ортогональную с функциями , и . Тогда функцию представим в форме , а коэффициенты ортогонализации найдутся из условий

(3.17)

Если сравнить коэффициенты и , то при интегрировании соотношений (3.17) в них и есть константы, а , и условия ортогонализации их совпадают и поэтому в новой функции отпадает необходимость использования дополнительной функции . Здесь коэффициенты можно принять в виде ; или и или . В случае полной ортогонализации функций разрешающие подсистемы (3.10) и (3.11) разделятся на две независимые и запишутся в форме

(3.18)

Первое уравнение системы (3.18) можно проинтегрировать. Поскольку , то при нагрузка есть нормальная погонная сила . Если , то , но . В данном случае это постоянная по длине и приложенная на краю панели сила, т.е. при интегрировании первого уравнения появляется константа интегрирования, которая по смыслу задачи есть нормальная сила, действующая вдоль панели. Поэтому эту константу можно сразу определить для балочной функции,

удовлетворяя условию на границе, так как константа интегрирования будет равна силе . После интегрирования первое уравнение (3.18) примет вид

или .

Подстановка во второе уравнение (3.18) дает разрешающее уравнение для функции :

.

Два последних уравнения системы (3.18) приводятся к уравнению

.

Решение приведенных уравнений будет рассмотрено ниже. Однако полная ортогонализация выбранных функций не для всех рассматриваемых задач дает нетривиальное решение, поэтому приведем вариант, когда между двумя системами остается связующий коэффициент . Для этого в решении отбросим функцию , тогда разрешаемая система примет вид

(3.19)

Для сравнения результатов, полученных с помощью представленных систем, рассмотрим также решение полной системы с ортогонализацией только первоначально выбранных функций перемещений и между собой:

(3.20)

И, наконец, рассмотрим решение полной связанной системы без ортогонализации функций и между собой:

(3.21)

Сравним решения представленных вариантов уравнений позднее.

Изгибаемая панель, нагруженная поперечными силами. Выбор аппроксимирующих функций задачи изгиба рассмотрен выше. Однако такой вид соответствует кососимметричным поперечным нагрузкам, действующим на краю панели. Для односторонне приложенной силы, например, на верхнем краю панели необходимо решить две отдельные задачи, изображенные на рис. 3.5, т.е. изгиб от кососимметричной нагрузки и сжатие конца балки симметрично приложенными силами. Вначале рассмотрим изгиб панели от кососимметричной нагрузки. Здесь функции и для продольных перемещений кососимметричны, а для поперечных – симметричны. Рассмотрим сначала вид уравнений с четырьмя выбранными функциями. С учетом вида первоначально выбранных функций можно увидеть, что ; ; , а между другими коэффициентами

Рис. 3.5. Вид несимметричного нагружения

существует связь ; ; и . Для того чтобы начальную систему уравнений привести к простому виду решения и выделить уравнение изгиба, проведем ортогонализацию функций и между собой. Представим функции и в виде и . В этом случае коэффициенты ортогонализации будут найдены и удовлетворят условиям и . При этом будут равны нулю коэффициенты . Таким образом, с учетом всех упрощений для коэффициентов системы (3.10) и (3.11) примут вид

(3.22)

Первые два уравнения соответствуют изгибу балки с учетом поперечной деформации. Аналитическое решение системы (3.22) не представляет затруднений, так как с помощью второго уравнения первое приводится к виду где – действующая поперечная сила, а в третьем исключаются неизвестные и . С помощью новой формы полученного первого уравнения из четвертого уравнения системы (3.22) исключим неизвестное . Тогда система примет окончательный для решения вид

(3.23)

где – изгибающий момент, действующий по длине панели и удовлетворяющий статическим граничным условиям при . Два последних соотношения сводятся к одному уравнению четвертого порядка относительно функции :

. (3.24)

Далее строятся решения для других трех функций, которые имеют вид

;

;

.

Решение этой системы будет рассмотрено позднее. Кроме того, там же для сравнения точности полученного решения сравним решение (3.24) с решением, в котором для функции перемещения 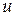будут взяты две дополнительные функции и . Однако в этом случае аналитического решения получить уже нельзя. Удастся выделить только балочную часть решения, а остальные уравнения придется решать совместно.

Приведенное выше решение соответствует кососимметричному расположению сил на краю панели (см. рис.3.5). Чтобы получить решение для панели, нагруженной силой, которая приложена с одной стороны края панели, необходимо сложить рассмотренное решение с решением для панели, нагруженной на краю симметрично действующими силами (см. рис.3.5). При рассмотрении второй симметричной задачи нагрузка, приложенная на границе панели, является самоуравновешенной и имеет только локальный эффект воздействия. Поэтому имеем затухающее решение только от этого края и условия закрепления панели на другом краю не окажут влияния на решение для достаточно длинной панели. Здесь основное перемещение направлено вдоль координаты 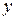и возможный вид этих функций показан на рис.3.6. Функция может быть выбрана как в линейной форме, так и в нелинейной. Однако, если необходимо учесть влияние второй границы (короткая панель или действует распределенная сжимающая нагрузка), решение необходимо дополнить функцией , которая учитывает условие закрепления (см. рис.3.1).

Поскольку все задаваемые функции учитывают депланацию поперечного сечения, то задача имеет простое аналитическое решение, когда учитываются по одной функции и вдоль каждого направления. Разрешающие уравнения имеют вид

. (3.25)

Решение этой системы не вызывает затруднений. Для случая, когда необходимо учесть влияние противоположного края панели, необходимо учесть в решении функцию (см. рис.3.6), а система уравнений примет вид

(3.26)

Рис. 3.6. Вид выбранных функций при действии сжимающих

сил (рис. 3.5)

Анализ системы показывает, что полную ортогонализацию системы проводить нельзя, так как в этом случае из решения выпадет функция . Поэтому рациональным будет ортогонализация функций, входящих в коэффициенты и . Кроме того, оказывается . Для этого функции и можно выбрать в виде ; . Здесь коэффициенты ортогонализации , а система уравнений запишется

(3.27)

Эту систему можно решать методом последовательных приближений. Для этого, например, используя решение предыдущей системы (3.25), можно получить решение для функции , которое затем пропустить через полную систему (3.26). Сложив решение задач (см. рис.3.5), получим решение поставленной задачи, т.е. решение от действия силы, приложенной с одной какой-то стороны панели. Видно, что такой подход позволяет учесть условия конкретного приложения нагрузки.

Из анализа рассмотренных выше решений задач видно, что простое решение можно получить, если депланация поперечного сечения учитывается не более чем одной функцией в каждом направлении. При увеличении числа функций депланаций решение усложняется тем, что повышается степень характеристического уравнения для определения корней дифференциальных уравнений разрешающей системы.

Приведем решение еще одной задачи, которое соответствует длинномерным панелям с относительно небольшой строительной высотой. Рассмотрим решение удлиненной панели, нагруженной поперечной кососимметричной нагрузкой (см. рис.3 .5), в которой пренебрежем поперечным обжатием сечения. Здесь для решения выберем три функции : , которая учитывает перемещение сечения панели как балки, и и , учитывающие депланацию сечения и условия точечного закрепления одного края. Коэффициенты ортогонализации определяются при удовлетворении условий ; и . Функция поперечного перемещения учитывает только недеформируемое поперечное смещение сечения. В этом случае разрешающая система имеет вид

.

С учетом того, что между коэффициентами существует связь ; ; , первое и четвертое уравнения приводятся к виду

;

.

Исключая функции и из второго и третьего уравнений, находим функции и , сводя их к одному разрешающему уравнению четвертого порядка относительно функции .

Рассмотренные решения характерны для большинства возможных практических задач для панелей и силового каркаса, например для лонжеронов и нервюр крыла самолетов. Позволяют выявлять места концентраций напряжений в краевых зонах, чтобы в дальнейшем уточнять изменение свойств материала за счет появления трещин, использовать полученные напряженные состояния в задачах устойчивости конструкций. Таким образом, построены математические расчетные модели для решения сформулированных задач.