Динамика материальной точки и
КИНЕМАТИКА ПОСТУПАТЕЛЬНОГО
И ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
1.Велосипедист проехал первую половину времени своего движения со скоростью u1 = 16 км/ч, вторую половину времени – со скоростью u2 = 12 км/ч. Определить среднюю скорость движения велосипедиста.
Ответ: 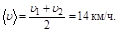
2.Точка прошла половину пути со скоростью u0. На оставшейся части пути она половину времени двигалась со скоростью u1, а последний участок прошла со скоростью u2. Найти среднюю за все время движения скорость точки.
Ответ: 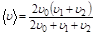 .
.
3.За промежуток времени t точка прошла половину окружности радиуса R. Вычислить за это время: а) среднее значение модуля скорости 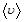 ; б) модуль среднего вектора скорости
; б) модуль среднего вектора скорости 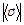 ; в) модуль среднего вектора полного ускорения
; в) модуль среднего вектора полного ускорения 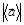 , если точка двигалась с постоянным тангенциальным ускорением.
, если точка двигалась с постоянным тангенциальным ускорением.
Ответ: а) 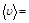
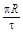 ;
;
б) 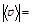
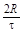 ;
;
в) 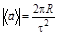 .
.
4.От бакена, который находится на середине широкой реки, отошли две лодки: А и В. Обе лодки стали двигаться по взаимно перпендикулярным прямым: лодка А – вдоль реки, а В – поперек. Удалившись на одинаковое расстояние от бакена, лодки вернулись затем обратно. Найти отношение времен движения лодок 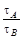 , если скорость каждой лодки относительно воды в h = 1,2 раза больше скорости течения.
, если скорость каждой лодки относительно воды в h = 1,2 раза больше скорости течения.
Ответ: 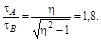
5.Из пункта А, находящегося на шоссе (cм. рис.), необходимо за кратчайшее время попасть на машине в пункт В, расположенный в поле на расстоянии l от шоссе. Известно, что скорость машины по полю в hраз меньше ее скорости по шоссе. На каком расстоянии от точки D следует свернуть с шоссе? Ответ: 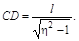 | 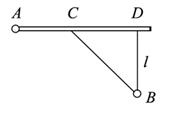 |
6.Зависимость пройденного телом пути от времени задается уравнением s = A–Bt+Ct2+Dt3, где A = 6,0 м, B = 3,0 м/с, C = 3,0 м/c2, D = 1,0 м/с3. Определить для тела в интервале времени от t1 = 1,0 с до t2 = 4,0 с: а) среднюю скорость 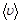 ; б) среднее ускорение
; б) среднее ускорение 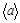 .
.
Ответ: а) 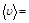
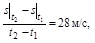
б) 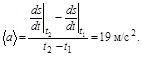
7.Радиус-вектор точки А относительно начала координат меняется со временем t по закону 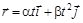 , где a и b – постоянные,
, где a и b – постоянные, 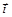 и
и 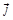 – орты осей x и y. Найти: а) уравнение траектории точки y (x), изобразить ее график; б) зависимости от времени скорости
– орты осей x и y. Найти: а) уравнение траектории точки y (x), изобразить ее график; б) зависимости от времени скорости 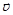 , ускорения
, ускорения 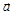 и модулей этих величин; в) зависимость от времени угла j между векторами
и модулей этих величин; в) зависимость от времени угла j между векторами 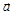 и
и 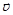 .
.
Ответ: а) 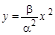 ;
;
б) 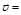
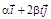 ,
, 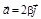 ,
, 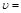
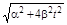 ,
, 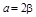 ;
;
в) 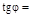
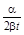 .
.
8.Точка движется в плоскости xy из положения с координатами x = y = 0, со скоростью 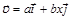 , где a и b – постоянные,
, где a и b – постоянные, 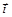 и
и 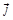 – орты осей x и y соответственно. Определить: а) уравнение траектории точки y (x); б) форму траектории.
– орты осей x и y соответственно. Определить: а) уравнение траектории точки y (x); б) форму траектории.
Ответ: а) 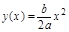 ; б) парабола.
; б) парабола.
9.Зависимость пройденного телом пути по окружности радиусом r = 3,0 м задается уравнением 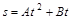 , где
, где 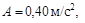 а
а 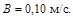 Определить для момента времени t = 1,0 с после начала движения следующие ускорения: а) нормальное; б) тангенциальное; в) полное.
Определить для момента времени t = 1,0 с после начала движения следующие ускорения: а) нормальное; б) тангенциальное; в) полное.
Ответ: а) 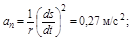
б) 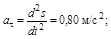
в) 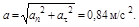
10.В момент t = 0 частица вышла из начала координат в положительном направлении оси х. Ее скорость меняется со временем по закону 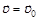
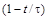 , где
, где 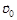 – начальная скорость, модуль которой u0 = 10 см/с, t = 5,0 с. Найти координату х частицы в момент времени 6,0; 10 и 20 с.
– начальная скорость, модуль которой u0 = 10 см/с, t = 5,0 с. Найти координату х частицы в момент времени 6,0; 10 и 20 с.
Ответ: x = u0t(1 – t/2t) и соответственно x = 0,24; 0 и –4,0 м.
11.Радиус-вектор частицы меняется со временем t по закону 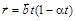 , где
, где 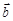 – постоянный вектор, a – положительная постоянная. Найти: а) скорость
– постоянный вектор, a – положительная постоянная. Найти: а) скорость 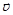 и ускорение
и ускорение 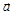 частицы в зависимости от времени; б) промежуток времени Dt, по истечении которого частица вернется в исходную точку, а также путь s, который она пройдет при этом.
частицы в зависимости от времени; б) промежуток времени Dt, по истечении которого частица вернется в исходную точку, а также путь s, который она пройдет при этом.
Ответ: a) 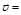
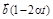 ,
, 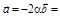 const;
const;
б) Dt = 1/a, s = b/2a.
12.Точка движется в плоскости xy по закону x = at, y = at (1 – bt), где a и b – положительные постоянные. Найти: а) уравнение траектории точки y (x); изобразить ее график; б) скорость u и ускорение а точки в зависи-мости от t; в) момент t0, когда угол между скоростью и ускорением равен p/4.
Ответ: а) y = x–x2b/a;
б) u = 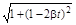 ; a = 2ba;
; a = 2ba;
в) t0 = 1/b.
13.Диск радиусом R = 10 см вращается так, что зависимость линейной скорости точек, лежащих на ободе диска , от времени задается уравне-нием 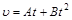 , где
, где 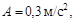 а
а 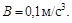 Определить момент времени, для которого вектор полного ускорения
Определить момент времени, для которого вектор полного ускорения 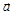 образует с радиусом колеса угол
образует с радиусом колеса угол 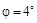 .
.
Ответ: t = 2 с.
14.Диск вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением 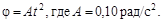 Определить полное ускорение a точки диска к концу второй секунды движения, если ее линейная скорость в этот момент u = 0,40 м/с.
Определить полное ускорение a точки диска к концу второй секунды движения, если ее линейная скорость в этот момент u = 0,40 м/с.
Ответ: 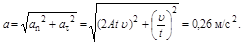
15.Твердое тело вращается вокруг неподвижной оси так, что угол его поворота меняется в зависимости от времени по закону 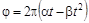 , где a и b – положительные постоянные. Найти момент времени t, в который тело останавливается, а также число оборотов N тела до остановки.
, где a и b – положительные постоянные. Найти момент времени t, в который тело останавливается, а также число оборотов N тела до остановки.
Ответ: 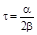 ,
, 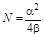 .
.
16.Твердое тело вращается вокруг неподвижной оси по закону j = at – bt3, где а и b – положительные постоянные. Найти: а) средние значения угловой скорости и углового ускорения за промежуток времени от t = 0 до остановки; б) угловое ускорение в момент остановки тела.
Ответ: а) <w> = 2а/3, <b> = 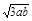 ;
;
б) b = 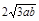 .
.
17.Твердое тело вращается, замедляясь, вокруг неподвижной оси с угловым ускорением b ~ 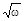 , где w – его угловая скорость. Найти среднюю угловую скорость тела за время, в течение которого оно будет вращаться, если в начальный момент его угловая скорость была равна w0.
, где w – его угловая скорость. Найти среднюю угловую скорость тела за время, в течение которого оно будет вращаться, если в начальный момент его угловая скорость была равна w0.
Ответ: 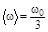 .
.
18.Круглый конус с углом полураствора a и радиусом основания R катится равномерно без скольжения по горизонтальной плоскости, как показано на рис. Вершина конуса закреплена шарнирно в точке О, которая находится на одном уровне с точкой С – центром основания конуса. Скорость точки С равна u. Найти модули:
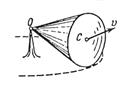 | а) угловой скорости конуса; б) углового ускорения конуса. Ответ: а) w = u / (R cos a); б) 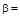 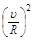 tg a. tg a. |
ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ И
