Задания для выполнения контрольных работ. Общее количество контрольных работ и число контрольных работ в семестре, которые должен выполнить студент той или иной специальности
Общее количество контрольных работ и число контрольных работ в семестре, которые должен выполнить студент той или иной специальности, определяется Учебным планом этой специальности. Объем контрольной работы, а также, какие именно задания входят в ту или иную контрольную работу, определяется решением кафедры высшей математики и лектор доводит эти сведения до студентов.
Каждое задание содержит 10 вариантов. Студент выбирает вариант, номер которого совпадает с последней цифрой номера его студенческого билета (зачетной книжки).
При оформлении контрольной работы необходимо записать условие каждого задания и привести его решение в полном объеме со всеми необходимыми теоретическими ссылками и объяснениями. Решение должно в обязательном порядке заканчиваться соответствующим ответом или ответами на все вопросы задачи.
Элементы линейной алгебры и аналитической геометрии
Задание 1.
1-10. Решить данную систему следующими методами: а) методом Крамера, в) матричным методом.
1. 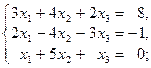 | 6. 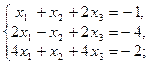 |
2. 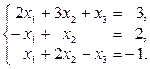 | 7. 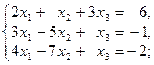 |
3. 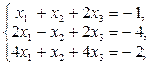 | 8. 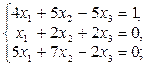 |
4. 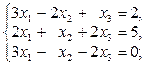 | 9. 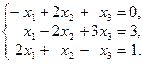 |
5. 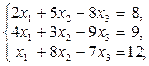 | 10. 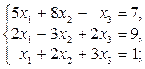 |
Задание 2.
11-20. Выясните, образуют ли вектора  ,
,  ,
, 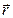 базис. Если образуют, то разложить вектор
базис. Если образуют, то разложить вектор 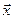 по этому базису.
по этому базису.
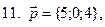
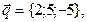
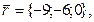
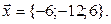
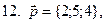
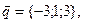
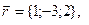
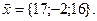
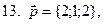
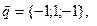
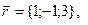
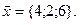
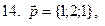
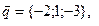
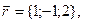
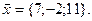
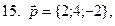
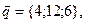
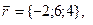
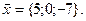
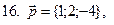
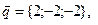
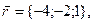
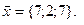
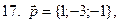
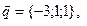

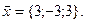
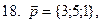
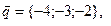
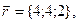
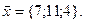
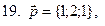
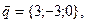
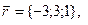
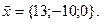
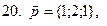
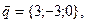
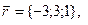
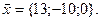
Задание 3.
21-30. Даны координаты вершин пирамиды 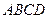 . Сделать чертеж и найти:
. Сделать чертеж и найти:
1) Длину ребра 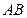
2) Угол между ребрами 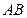 и
и 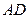
3) Угол между ребром 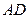 и гранью
и гранью 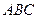
4) Площадь грани 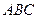
5) Объем пирамиды 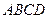
6) Уравнение прямой 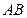
7) Уравнение плоскости 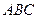
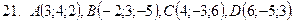
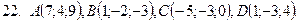
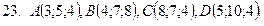
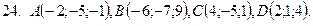
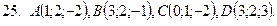
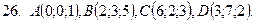
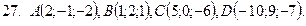
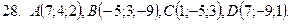
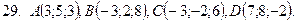
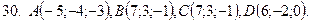
Задание 4.
31-40. Решить задачу
31. Составить уравнения сторон треугольника, зная одну его вершину 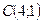 , уравнение высоты
, уравнение высоты 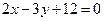 и медианы
и медианы 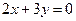 , проведенных из одной вершины.
, проведенных из одной вершины.
32. Найти длины высот треугольника, стороны которого имеют уравнения 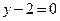 ,
, 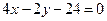 ,
, 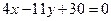 .
.
33. Найти уравнения прямых, параллельных данной прямой 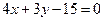 и отстоящих от нее на расстоянии
и отстоящих от нее на расстоянии 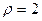 .
.
34. Даны две точки 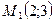 и
и 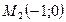 . Составить уравнение прямой, проходящей через точку
. Составить уравнение прямой, проходящей через точку 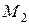 перпендикулярно отрезку
перпендикулярно отрезку 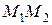 . Записать уравнение прямой в параметрическом виде.
. Записать уравнение прямой в параметрическом виде.
35. Записать общее уравнение прямой, проходящей через две точки 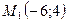 и
и 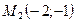 . Найти угловой коэффициент этой прямой.
. Найти угловой коэффициент этой прямой.
36. Даны две смежные вершины параллелограмма 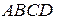
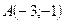 и
и 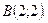 Точка
Точка 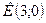 – точка пересечения его диагоналей. Составить уравнения сторон.
– точка пересечения его диагоналей. Составить уравнения сторон.
37. Даны две вершины 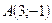 и
и 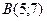 треугольника
треугольника 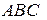 и точка пересечения его высот
и точка пересечения его высот 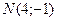 . Составить уравнения сторон этого треугольника.
. Составить уравнения сторон этого треугольника.
38. Через точки 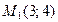 и
и 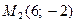 проведена прямая. Найти точки пересечения этой прямой с осями координат.
проведена прямая. Найти точки пересечения этой прямой с осями координат.
39. На прямую, проходящую через точки 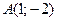 и
и 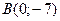 опущен перпендикуляр из точки
опущен перпендикуляр из точки 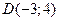 . Вычислить длину этого перпендикуляра.
. Вычислить длину этого перпендикуляра.
40. Написать параметрические уравнения прямой, проходящей через точки 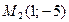 и
и 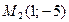 ; найти угловой коэффициент этой прямой.
; найти угловой коэффициент этой прямой.
Задание 5.
41-50. Привести уравнение кривой второго порядка к каноническому виду и построить ее. Указать координаты вершин и фокусов.
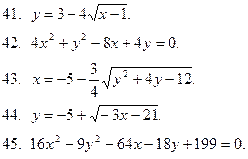 | 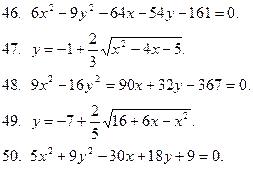 |
Задание 6.
51-60. Построить кривую в полярной системе координат
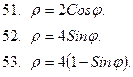
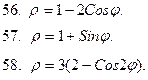
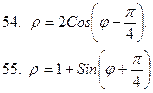 | 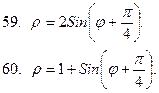 |
Задание 7.
61-70.Дано комплексное число 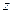 . Записать число
. Записать число 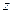 в алгебраической и тригонометрической формах.
в алгебраической и тригонометрической формах.
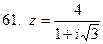 | 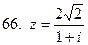 |
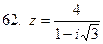 | 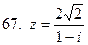 |
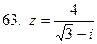 | 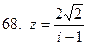 |
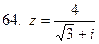 | 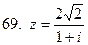 |
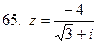 | 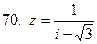 |
Введение в математический анализ
Задание 8.
71-80.Найти пределы функций, не пользуясь правилом Лопиталя.
| 71. | а) 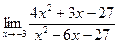 | б) 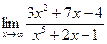 |
в) 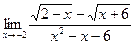 | г) 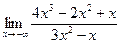 | |
д) 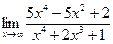 | е) 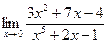 | |
ж) 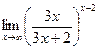 | ||
| 72. | а) 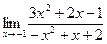 | б) 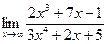 |
в) 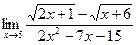 | г) 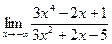 | |
д) 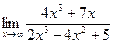 | е) 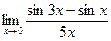 | |
ж) 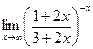 | ||
| 73. | а) 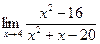 | б) 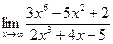 |
в) 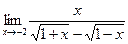 | г) 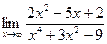 | |
д) 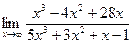 | е) 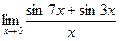 | |
ж) 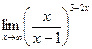 | ||
| 74. | а) 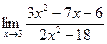 | б) 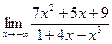 |
в) 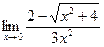 | г) 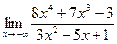 | |
д) 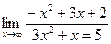 | е) 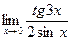 | |
ж) 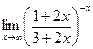 | ||
| 75. | а) 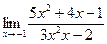 | б) 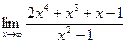 |
в) 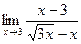 | г) 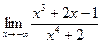 | |
д) 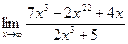 | е) 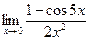 | |
ж) 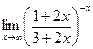 | ||
| 76. | а) 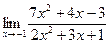 | б) 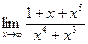 |
в) 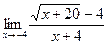 | г) 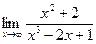 | |
д) 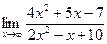 | е) 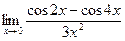 | |
ж) 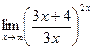 | ||
| 77. | а) 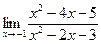 | б) 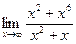 |
в) 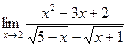 | г) 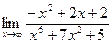 | |
д) 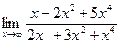 | е) 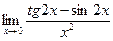 | |
ж) 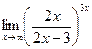 | ||
| 78. | а) 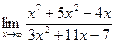 | б) 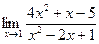 |
в) 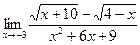 | г) 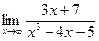 | |
д) 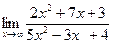 | е) 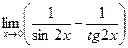 | |
ж) 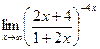 | ||
| 79. | а) 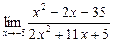 | б) 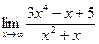 |
в) 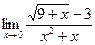 | г) 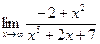 | |
д) 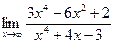 | е) 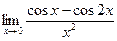 | |
ж) 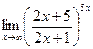 | ||
| 80. | а) 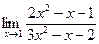 | б) 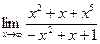 |
в) 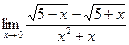 | г) 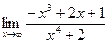 | |
д) 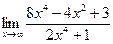 | е) 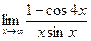 | |
ж) 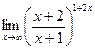 |
Задание 9.
81-90. Исследовать на непрерывность, выяснить характер точек разрыва и изобразить графически следующие функции
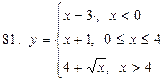 | 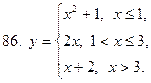 |
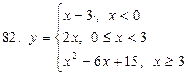 | 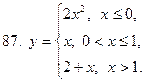 |
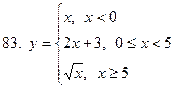 | 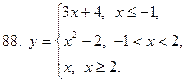 |
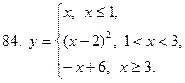 | 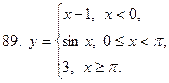 |
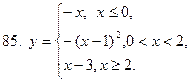 | 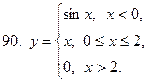 |
Задание 10.
91-100. Найти производные следующих функций:
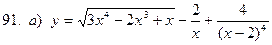 | 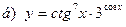 | |||||
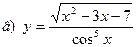 | 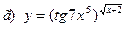 | |||||
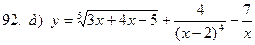 | 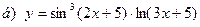 | |||||
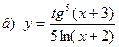 | 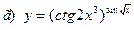 | |||||
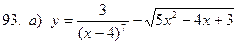 | 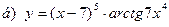 | |||||
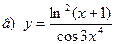 | 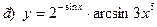 | |||||
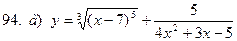 | 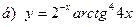 | |||||
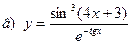 | 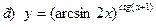 | |||||
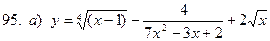 | 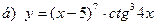 | |||||
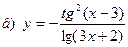 | 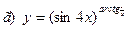 | |||||
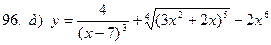 | 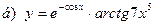 | |||||
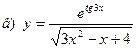 | 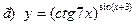 | |||||
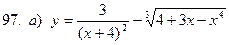 | 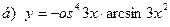 | |||||
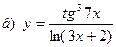 | 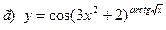 | |||||
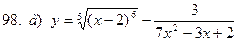 | 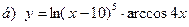 | |||||
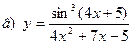 | 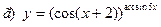 | |||||
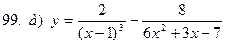 | 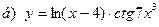 | |||||
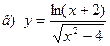 | 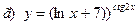 | |||||
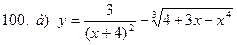 | 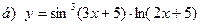 | |||||
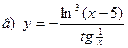 | 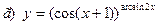 | |||||
Задание 11.
101-110. Найти 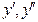 для функции, заданной параметрически:
для функции, заданной параметрически:
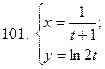 | 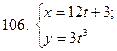 |
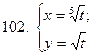 | 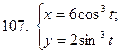 |
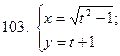 | 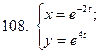 |
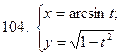 | 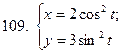 |
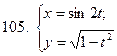 | 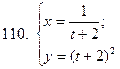 |
Задание 12.
111-120. Исследовать методами дифференциального исчисления функцию 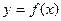 . На основании результатов исследования построить график этой функции.
. На основании результатов исследования построить график этой функции.
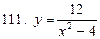 | 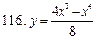 |
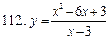 | 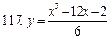 |
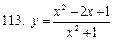 | 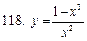 |
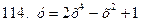 | 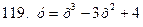 |
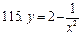 | 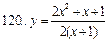 |
Задание 13.
121-130.Найти частные производные 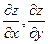 функции z=f(x;y)
функции z=f(x;y)
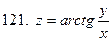 | 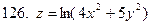 |
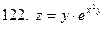 | 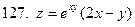 |
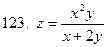 | 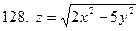 |
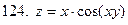 | 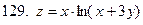 |
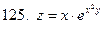 | 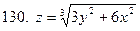 |
Задание 14.
131-140.Найти неопределенные интегралы.
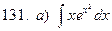 | б) 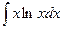 |
в) 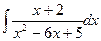 | г) 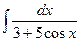 |
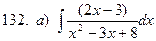 б)
б) 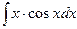
в) 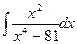 г)
г) 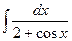
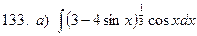 б)
б) 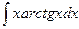
в) 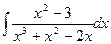 г)
г) 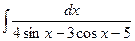
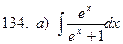 б)
б) 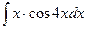
в) 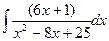 г)
г) 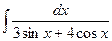
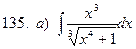 б)
б) 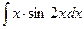
в) 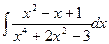 г)
г) 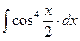
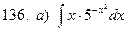 б)
б) 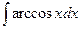
в) 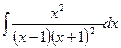 г)
г) 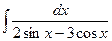
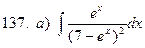 б)
б) 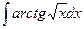
в) 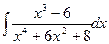 г)
г) 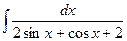
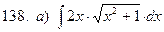 б)
б) 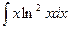
в) 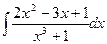 г)
г) 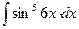
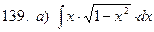 б)
б) 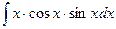
в) 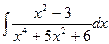 г)
г) 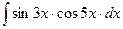
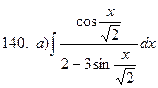 б)
б) 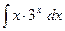
в) 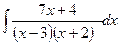 г)
г) 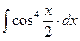
Задание 15.
141-150.Вычислить площадь плоской фигуры, ограниченной указанными линиями. Сделать чертеж.
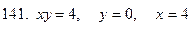
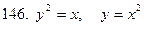
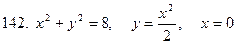
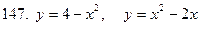
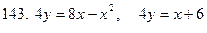
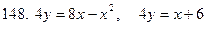
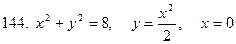
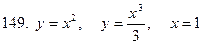
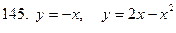
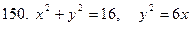
Задание 16.
151- 160.Вычислить объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной данными линиями.
151. Параболой 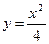 , прямой
, прямой 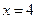 и осью Ох.
и осью Ох.
152. Полуэллипсом 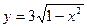 , параболой
, параболой 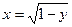 и осью Оy.
и осью Оy.
153.Параболой 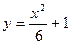 и прямыми
и прямыми 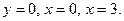
154. Параболами 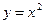 и
и 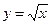 .
.
155. Гиперболой 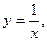 и прямыми
и прямыми 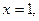
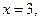
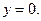
156. Осью Ох и параболой 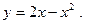
157. Параболой 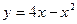 и прямыми
и прямыми 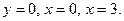
158. Линиями 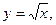
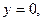
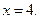
159. Параболой 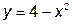 и осью Oх.
и осью Oх.
160. Параболой 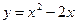 и осью Oх.
и осью Oх.
Задание 17.
161-170.Вычислить несобственный интеграл или доказать его расходимость.
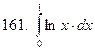
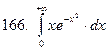
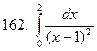
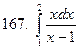
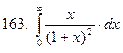
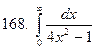
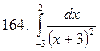
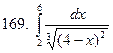
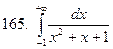
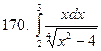
Задание 18.
171-180.Найти общее решение дифференциального уравнения первого порядка.
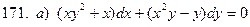
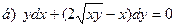
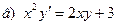
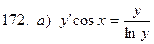
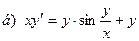
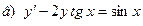
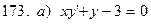
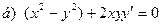
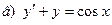
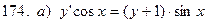
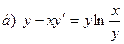
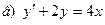
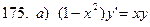
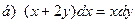
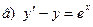
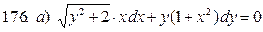
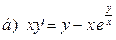
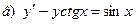
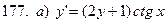
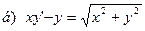
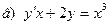
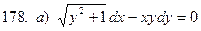
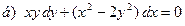
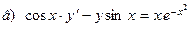
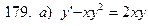
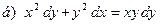
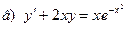
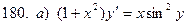
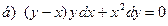
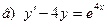
Задание 19.
181-190.Найти общее решение дифференциального уравнения второго порядка, допускающего понижение порядка
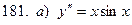
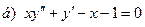
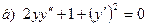
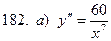
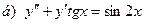
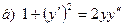
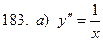
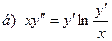
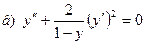
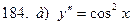
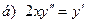
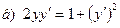
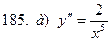
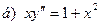
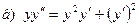
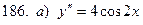
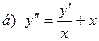
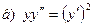
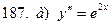
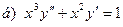
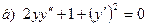
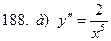
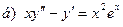
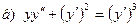
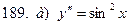
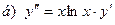
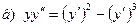
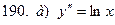
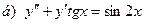
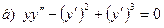
Задание 20.
191-200. Решить задачу Коши
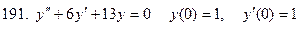
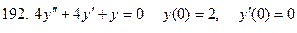
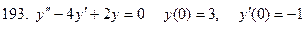
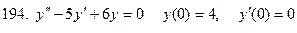
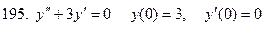
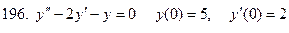
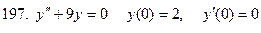
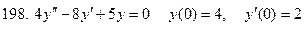
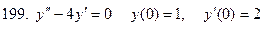
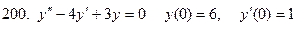
Задание 21.
201-210. Решить линейное неоднородное дифференциальное уравнение:
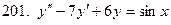
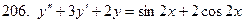
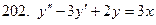
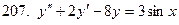
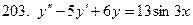
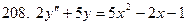
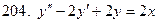
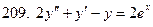
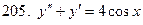
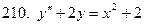
Задание 22.
211-220.Решить систему дифференциальных уравнений
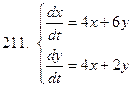 | 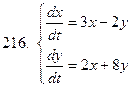 |
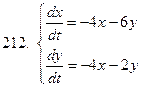 | 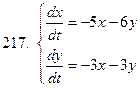 |
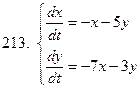 | 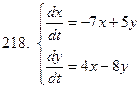 |
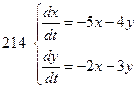 | 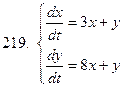 |
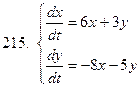 | 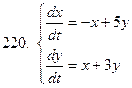 |
Задание 23.
221-230.С помощью двойного интеграла вычислить площадь фигуры, ограниченной линиями.
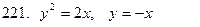 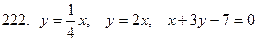 |
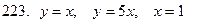
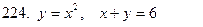
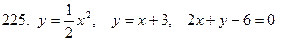
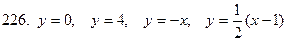
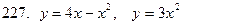
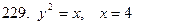
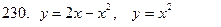
Задание 24.
231-240. С помощью тройного интеграла вычислить объем тела, ограниченного указанными поверхностями. Сделать чертеж проекции данного тела на плоскость Оху.
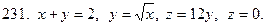
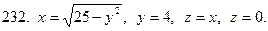
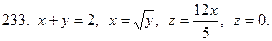
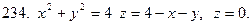
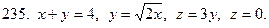
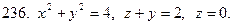
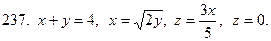
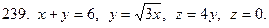
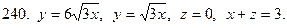
Задание 25.
241-250. Вычислить криволинейный интеграл первого рода
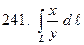 , если
, если 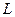 – дуга окружности
– дуга окружности 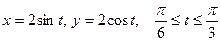 .
.
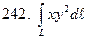 по кривой
по кривой 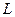 :
: 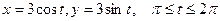 .
.
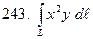 по кривой
по кривой 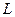 :
: 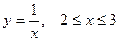 .
.
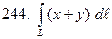 по кривой
по кривой 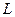 :
: 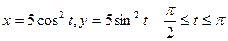 .
.
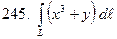 по кривой
по кривой 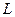 :
: 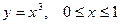 .
.
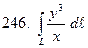 по кривой
по кривой 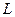 :
: 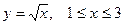 .
.
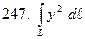 по кривой
по кривой 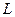 :
: 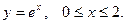
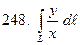 , если
, если 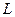 – дуга параболы
– дуга параболы 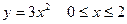 .
.
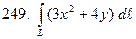 , если
, если 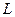 –дуга окружности
–дуга окружности 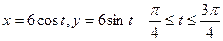 .
.
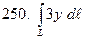 , если
, если 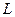 – дуга кубической параболы
– дуга кубической параболы 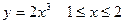 .
.
Задание 26.
251-260. Вычислить криволинейный интеграл второго рода
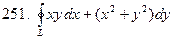 , где
, где 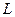 – контур четырехугольника АВСD с вершинами А(-1,0), В(1,0), С(2,1), D(2,2) при положительном направлении обхода.
– контур четырехугольника АВСD с вершинами А(-1,0), В(1,0), С(2,1), D(2,2) при положительном направлении обхода.
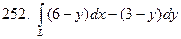 , где
, где 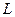 – арка циклоиды
– арка циклоиды
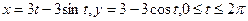 .
.
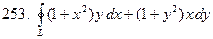 , где
, где 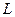 – контур треугольника АВС с вершинами А(0,0), В(2,0), С(4,2) при положительном направлении обхода.
– контур треугольника АВС с вершинами А(0,0), В(2,0), С(4,2) при положительном направлении обхода.
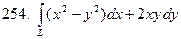 , где
, где 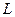 – дуга параболы
– дуга параболы 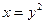 при
при 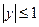 .
.
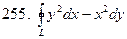 , где
, где 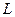 – контур треугольника ОАВ с вершинами О(0,0), А(2,2), В(0,2) при положительном направлении обхода.
– контур треугольника ОАВ с вершинами О(0,0), А(2,2), В(0,2) при положительном направлении обхода.
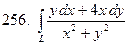 , где
, где 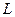 – отрезок прямой от точки А(1,2) до точки В(2,8).
– отрезок прямой от точки А(1,2) до точки В(2,8).
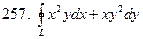 , где
, где 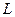 – дуга эллипса
– дуга эллипса 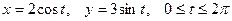 при положительном направлении обхода.
при положительном направлении обхода.
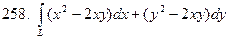 , где
, где 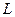 - дуга параболы
- дуга параболы 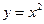 при
при 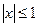 при положительном направлении обхода
при положительном направлении обхода
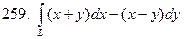 вдоль ломаной
вдоль ломаной 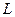 =ОАВ где О(0,0), А(2,0), В(4,5)
=ОАВ где О(0,0), А(2,0), В(4,5)
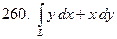 , где
, где 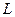 – четверть дуги окружности
– четверть дуги окружности 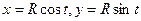 , лежащая в первой координатной четверти при положительном направлении обхода.
, лежащая в первой координатной четверти при положительном направлении обхода.
Задание 27.
261-270. Даны векторное поле 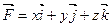 и плоскость
и плоскость 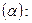 Ах+Ву+Сz+D=0, которая совместно с координатными плоскостями образует пирамиду
Ах+Ву+Сz+D=0, которая совместно с координатными плоскостями образует пирамиду 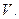 Пусть
Пусть 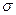 - основание пирамиды, принадлежащие плоскости
- основание пирамиды, принадлежащие плоскости 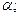
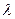 - контур, ограничивающий
- контур, ограничивающий 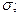 n-нормаль к
n-нормаль к 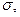 направленная вне пирамиды
направленная вне пирамиды 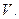 Вычислить:
Вычислить:
1) поток векторного поля 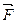 через поверхности
через поверхности 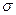 в направлениинормали n;
в направлениинормали n;
2) циркуляцию векторного поля 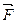 по замкнутому контуру
по замкнутому контуру 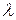 непосредственно и применив формулу Стокса к контуру
непосредственно и применив формулу Стокса к контуру 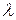 и ограниченной им поверхности
и ограниченной им поверхности 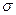 с нормалью n;
с нормалью n;
3) поток векторного поля 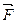 через полную поверхность пирамиды
через полную поверхность пирамиды 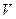 в направлении внешней нормали к ее поверхности непосредственно и по формуле Остроградского. Сделать чертеж.
в направлении внешней нормали к ее поверхности непосредственно и по формуле Остроградского. Сделать чертеж.
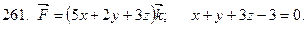
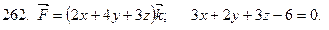
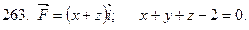
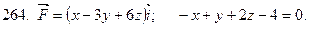
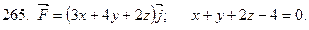
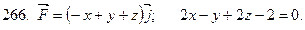
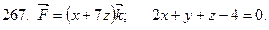
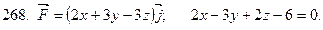
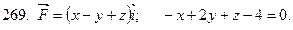
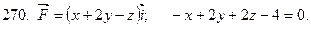
Задание 28.
