Прямая, как линия пресечения двух плоскостей
Даны две плоскости: 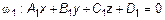 и
и 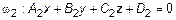 с перпендикулярами
с перпендикулярами 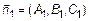 и
и 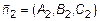 . Пусть эти плоскости пересекаются. Пересечение плоскостей образует прямую
. Пусть эти плоскости пересекаются. Пересечение плоскостей образует прямую 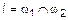 . Т. е.
. Т. е. 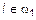 и
и 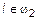 . Следовательно, общее уравнение прямой l будет определятся системой уравнений
. Следовательно, общее уравнение прямой l будет определятся системой уравнений
| |
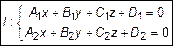 . (8)
. (8) 3.1. Переход от общего уравнения прямой к каноническому
Поскольку 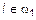 и
и 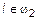 , то
, то 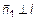 и
и 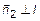 . Следовательно
. Следовательно 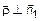 и
и 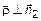 . То есть
. То есть 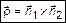 . Решим систему (8). Поскольку плоскости пересекаются
. Решим систему (8). Поскольку плоскости пересекаются 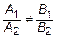 , то
, то 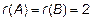 . Свободных неизвестных: 3-2=1. Пусть
. Свободных неизвестных: 3-2=1. Пусть 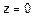 , тогда, подставляя ее в (8), получим систему уравнений определяющих точку прямой
, тогда, подставляя ее в (8), получим систему уравнений определяющих точку прямой 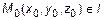 .
.
ПРИМЕР 1.
Прямая задана системой 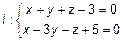 . Представим это уравнение в каноническом виде. Определим направляющий вектор
. Представим это уравнение в каноническом виде. Определим направляющий вектор
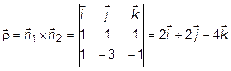 .
.
Определим точку 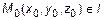 . Примем
. Примем 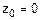 .
.
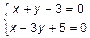 .
.
Вычитаем из первого уравнения второе и получим 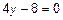 , откуда
, откуда 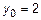 ,
, 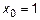 , а точка
, а точка 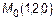 , а уравнение прямой в каноническом виде
, а уравнение прямой в каноническом виде
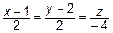 .
.
3.2. Переход от канонического уравнения прямой к общему
Запишем (7) в виде системы уравнений
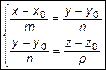 . (9)
. (9)
| |
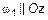 и
и 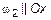 или двумя плоскостями, параллельными двум координатным осям.
или двумя плоскостями, параллельными двум координатным осям. 4. Угол между двумя прямыми в пространстве
Заданы две прямые в пространстве 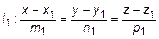 и
и 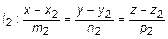 . Определим угол
. Определим угол 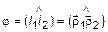 . Угол между прямыми определяется углом между направляющими векторами
. Угол между прямыми определяется углом между направляющими векторами
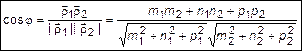 . (10)
. (10)
4.1. Условие перпендикулярности прямых
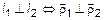 или
или 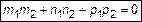 .
.
4.2. Условие параллельности прямых
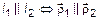 или
или 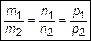 .
.
5. Угол прямой с плоскостью
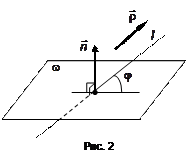 Дана плоскость
Дана плоскость 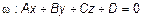 и прямая
и прямая
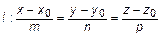 .
.
Определение 1.
Углом прямой с плоскостью называется угол, образованный этой прямой и ее проекцией на плоскость 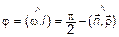 .
.
Учитывая 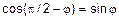 и правило скалярного произведения, определим
и правило скалярного произведения, определим
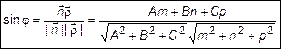 . (10)
. (10)
| |
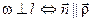 или
или 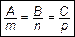 .
.
5.2. Условие параллельности прямой и плоскости
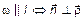 или
или 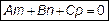 .
.
ПРИМЕР 2.
Даны: 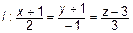 и
и 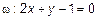 . Их расположение:
. Их расположение:
а) 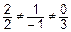
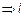 и
и 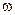 не перпендикулярны.
не перпендикулярны.
б) 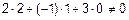
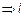 и
и 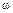 не параллельны.
не параллельны.
в) 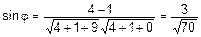 .
.
6. Точка пересечения прямой и плоскости
Дана плоскость 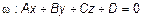 и прямая
и прямая 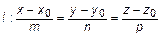 . Тогда точка пересечения будет определяться системой уравнений
. Тогда точка пересечения будет определяться системой уравнений
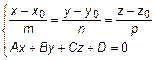 =
= 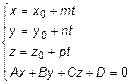 . (11)
. (11)
Откуда 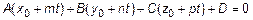 ,
,
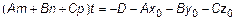 .
.
Рассмотрим три случая:
1. Если 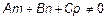 , то
, то 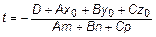 . Тогда t подставляем в (11).
. Тогда t подставляем в (11).
2. Если 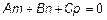 и
и 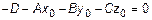 , тогда t – множество и
, тогда t – множество и 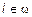 .
.
3. Если 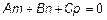 , но
, но 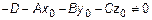 , тогда решений нет и l не пересекает
, тогда решений нет и l не пересекает 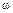 , т. е.
, т. е. 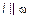 .
.
| |
Даны: точка 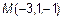 и плоскость
и плоскость 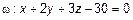 . Определить точку проекции М1на плоскость. Определим их положение.
. Определить точку проекции М1на плоскость. Определим их положение.
Запишем с учетом 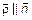 уравнение прямой, проходящей через точку М
уравнение прямой, проходящей через точку М 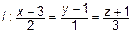 , тогда точка пересечения будет определяться системой
, тогда точка пересечения будет определяться системой 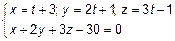 , откуда
, откуда 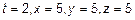 . Т. е.
. Т. е. 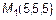 .
.
Заключение
В лекции рассматривалось уравнение прямой в пространстве. Важно понять, что плоскость – это частный случай уравнения прямой. Отметим, что условия параллельности и перпендикулярности прямых в пространстве аналогичны условиям для плоскостей. При определении прямой как линии пересечения двух плоскостей необходимо знать правило векторного умножения. В следующей лекции будет рассматриваться частный случай прямой в декартовой системе координат на плоскости. Отметим следующее:
- в каноническом уравнении прямой в пространстве двойное равенство;
- общее уравнение прямой в пространстве задается системой двух уравнений плоскости в пространстве;
- если в уравнении прямой отсутствует переменная, то это уравнение плоскости в 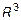 ;
;
- угол между плоскостями определяется на основе скалярного произведения векторов нормалей к плоскостям;
- угол между прямой и плоскостью определяется не через косинус, а через синус угла;
- при определении точки пересечения прямой и плоскости необходимо решать систему уравнений.
Литература
1. Рыжков В.В. Лекции по аналитической геометрии. - М.: Факториал пресс, 2000. – 208 с.
2. Ефимов Н.В. Краткий курс аналитической геометрии. – М.: Физматлит, 2002.
3. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. – М.: Наука, 1989, - 659 с.
| |
