Основные расчетные соотношения. В нелинейных элементах (НЭ) электрической цепи нелинейно связаны между собой ток и напряжение (в сопротивлении)

В нелинейных элементах (НЭ) электрической цепи нелинейно связаны между собой ток и напряжение (в сопротивлении), заряд и напряжение (в емкости), потокосцепление и ток (в индуктивности). В четвертой самостоятельной работе выполняются расчеты резистивных цепей, имеющих нелинейную вольт-амперную характеристику (ВАХ).

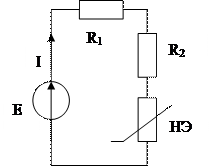
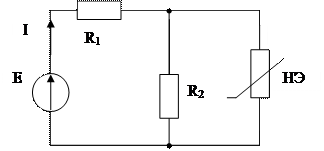
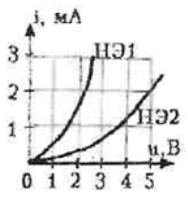
В ряде случаев исследование процессов в простейших нелинейных резистивных цепях удается провести без составления уравнений электрического равновесия, используя графические методы их анализа. Например, при последовательном соединении двух нелинейных сопротивлений (Рис. 3.1) графически суммируются их вольт-амперные характеристики и по результирующей ВАХ определяется протекающий через них ток по приложенному к цепи напряжению. Найденное значение тока, по ВАХ нелинейных элементов далее позволяет определить напряжение на каждом из них.

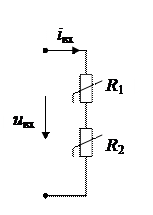
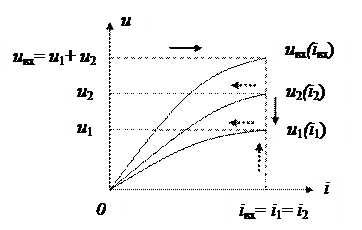
Рис. 3.1 - Определение напряжения на последовательно соединенных резистивных НЭ

Аналогично поступают и при большем количестве соединенных последовательно сопротивлений, некоторые из которых могут быть линейными (имеют линейную ВАХ). В результате таких преобразований нелинейные элементы заменяются одним с суммарной ВАХ. Если последовательно с НЭ в ветвь включен источник постоянной ЭДС, то ВАХ нелинейного элемента смещается вверх или вниз в соответствии с полярностью источника на величину его напряжения.

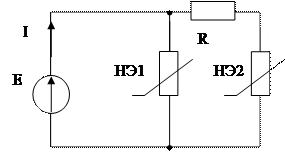
При параллельном соединении двух нелинейных сопротивлений суммируются зависимости i₁(u₁) и i₂(u₂) для получения ВАХ i_вх(u_вх) нелинейного сопротивления, которым можно заменить исследуемый участок цепи (Рис. 3.2).

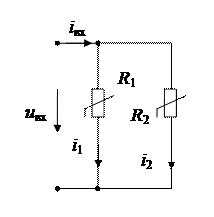
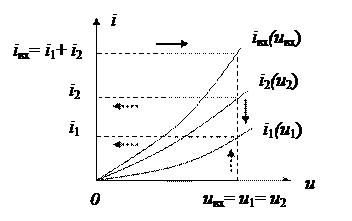
Рис. 3.2 - Определение тока через параллельно соединенные резистивные НЭ

При параллельном подключении к НЭ источника постоянного тока результирующая ВАХ смещается вверх-вниз в соответствие с направлением и величиной тока источника.

В ряде случаев, заданные в виде таблиц и графиков экспериментальные ВАХ описывают приближенными аналитическими соотношениями - аппроксимациями. В качестве аппроксимаций нелинейных ВАХ применяются: кусочно-линейная, полиномиальная, экспоненциальная, трансцендентными функциями и некоторые другие. При выполнении заданий четвертой самостоятельной работы используются полиномиальная и кусочно-линейная аппроксимации.

Вид аппроксимирующей функции должен определяться исходя из соотношения входного сигнала и вольт-амперной характеристики НЭ. Отметим, что при работе с режимом отсечки тока должна использоваться кусочно-линейная аппроксимация – это так называемый существенно-нелинейный режим работы. При этом ВАХ нелинейного элемента представляется в виде

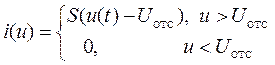,(3.1)

где U_отс – напряжение отсечки или напряжение начала характеристики,

u(t) =U_см +U_m cos w₀t.

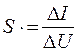– крутизна линейного участка вольт-амперной характеристики.

Следует отметить, что U_отс и S являются параметрами аппроксимирующего ВАХ полинома первой степени.

При гармоническом воздействии в этом режиме работы на выходе нелинейного элемента присутствует бесконечное количество гармоник, кратных частоте входного сигнала. Амплитуды этих гармонических составляющих определяются через амплитуду входного сигнала U_m с использованием коэффициентов Берга в соответствие с выражением

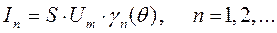(3.2)

Сами же коэффициенты Берга могут быть определены с использованием соотношения

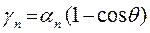, (3.3)

где коэффициенты 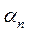представлены графически (Рис.2.3), а угол отсечки 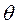определяется выражением

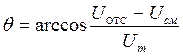(3.4)

в котором 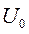- напряжение смещения.

Рис. 2.3 - Зависимость коэффициентов Берга от угла отсечки

В слабо-нелинейном режиме работы (без отсечки тока) используется полиномиальная аппроксимация

i(t) =а₀+a₁(U(t) –U₀)+a₂(U(t)–U₀)²+…+a_n(U(t)–U₀)ⁿ (3.5)

Здесь амплитуды гармоник определяются в виде

и т.д. В которой коэффициенты аппроксимации 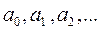определяются

в результате решения системы уравнений (число уравнений равно числу неизвестных коэффициентов), составленных по ВАХ для пар точек u,i равномерно расположенных в диапазоне аппроксимации характеристики.

Средняя крутизна нелинейного элемента по первой гармонике в этом случае равна

S₁ = I₁ / U_m = a₁+2a₂E+3a₃E²+ 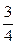a₃E³+ …, (3.6)

где I₁ - амплитуда первой гармонии тока стока, E = U_см –U₀.

Приложение 1

Метод трех и пяти ординат .

Формулы трех ординат позволяют вычислить постоянную составляющую I₀ и амплитуды двух гармоник I₁, I₂:

I₀ = (i_max + i_min + 2I₀)/4

I₁ = (i_max - i_min)/2 (П 1.1)

I₂ = (i_max + i_min - 2i₀)/4

где i_max, i_min, i₀ - значение тока соответственно при управляющем напряжении (на затворе полевого транзистора) u = E + U_m, при u = E - U_m, при u = E.

Здесь E - напряжение смещения в выбранной рабочей точке, U_m - амплитуда гармонического нпряжения на затворе.

Формулы пяти ординат позволяют найти:

I₀ = (i_max + i_min + 2(i₁ +i₂) )/6

I₁ = (i_max - i_min + (i₁ - i₂))/3

I₂ = (i_max + i_min - 2i₀)/4 (П1.2)

I₃ = (i_max - i_min - 2(i₁ - i₂))/6

I₄ = (i_max + i_min - 4(i₁ +i₂) + 6i₀)/12

Приложение 2

Коэффициенты разложения g_n(q) для последовательности косинусоидальных импульсов

q0	соs q	100g0	100g1	100g2	100g3	100g4	100g5
	0.996	0.007	0.014	0.014	0.014	0.014	0.014
	0.985	0.056	0.112	0.111	0.109	0.107	0.104
	0.966	0.189	0.376	0.368	0.355	0.338	0.317
	0.940	0.446	0.881	0.840	0.798	0.730	0.648
	0.906	0.865	1.697	1.602	1.452	1.258	1.037
	0.866	1.482	2.883	2.653	2.297	1.857	1.378
	0.819	2.33	4/49	4.00	3.28	2.42	1.55
	0.766	3.44	6.55	5.64	4.32	2.84	1.46
	0.707	4.83	9.09	7.50	5.31	3.00	1.06
	0.643	6.53	12.1	9.54	6.13	2.82	0.357
	0.574	8.59	15.6	11.7	6.69	2.27	-0.493
	0.5	10.9	19.6	13.8	6.89	1.38	-1.38
	0.423	13.6	23.9	15.8	6.68	0.226	-2.01
	0.342	16.6	28.7	17.6	6.02	-1.05	-2.49
	0.259	20.0	33.7	19.1	4.95	- 2.29	-2.44
	0.174	23.6	39.0	20.3	3.52	-3.22	-1.94
	0.087	27.6	44.4	21.0	1.83	-4.01	-1.08
	0.000	31.8	50.0	21.2	0.00	-4.24	0.00

Варианты заданий

Вариант №1 R1=R2=0,1 кОМ; Е=0,5 В; ВАХ НЭ известна. Определить значение тока I.

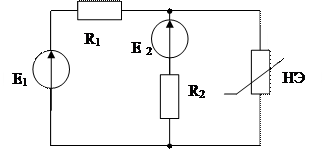
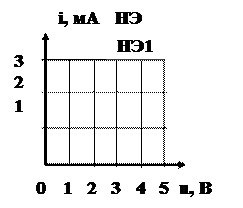
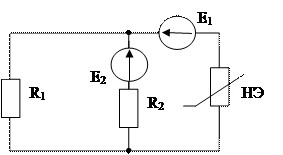
R1=1 кОм; R2=2 кОм, Е1=1 В, E2=4 В. ВАХ НЭ известна. Рассчитать ток, протекающий через НЭ.

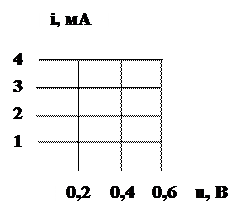
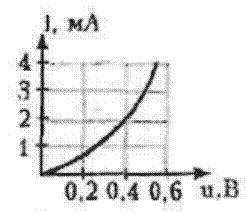
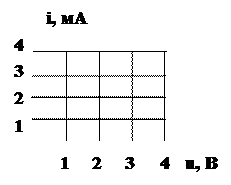
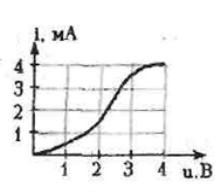
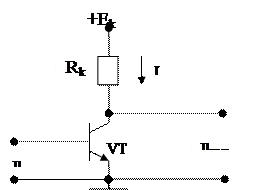
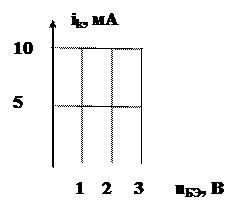
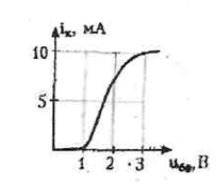
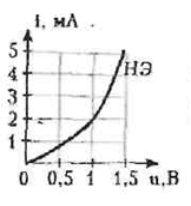
На вход усилителя подаётся напряжение uвх(t)=(1+cos10t) В. Проходная ВАХ транзистора известна. Построить график тока ik(ωt).

Для цепи и данных в задаче 3 записать функцию, аппроксимирующую рабочий участок ВАХ , и определить коэффициенты этой кусочно-линейной аппроксимации . Рис. 5

Рассчитать спектральные составляющие I0, I1, I2 тока ik для цепи в задаче 3. Построить спектр тока.

Вариант №2

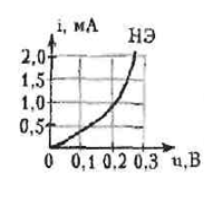R₁=600 Ом; R₂=50 Ом; Е=0,25 В; ВАХ НЭ известна. Определить ток I.

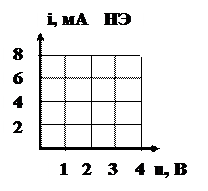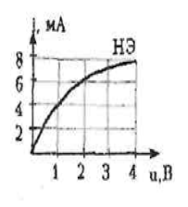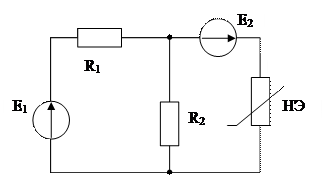
R₁= R₂=1 кОм; Е₁=2 В, E₂=3 В; ВАХ НЭ известна.

Рассчитать ток, протекающий через НЭ.

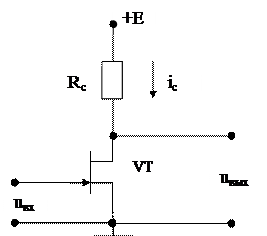
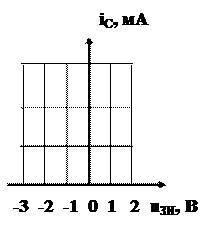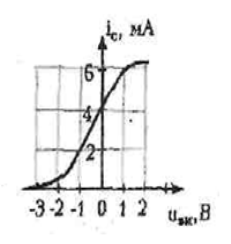На вход усилителя подаётся напряжение u_вх(t)=(-3+4cos100t), В.

Проходная ВАХ транзистора известна. Построить график тока i_С(ωt).

Для цепи и данных в задаче 3 записать функцию, аппроксимирующую рабочий участок ВАХ , и определить коэффициенты этой кусочно-линейной аппроксимации .

Рис. 5

Рассчитать спектральные составляющие I₀, I₁, I₂ тока i_С для цепи в задаче 3. Построить спектр тока.

Вариант №3 R=0,5 кОм, Е=2 В; ВАХ НЭ известны; Определить значение тока I.

R1= R2=1 кОм; Е1=2 В, E2=6 В; ВАХ НЭ известна. Наши рекомендации Напряжение, мощность и энергия. Пассивные и активные элементы электрической цепи Назовите основные разделы литературоведения и определите их функции в науке о литературе и то, как они связаны между собой. Синусоидальный ток в отдельных элементах электрической цепи Краткие теоретические сведения. Большинство промышленных и даже бытовых электрических сетей – трехфазные, в которых отдельные фазы цепи электрически связаны между собой Основные расчетные соотношения. Исходным положением для анализа переходного процесса в линейных электрических цепях является то, что переход реальной цепи от одного установившегося режима к Краткая теория. Под резонансом в электрической цепи понимают такое состояние цепи, когда ток и напряжение совпадают по фазе Мощность на элементах электрической цепи при гармоническом воздействии ЭДС и напряжение электрической цепи Способ снижения риска, предусматривающий распределение инвестированных средств между различными объектами вложения, которые не связаны между собой. ЭДС и напряжение в электрической цепи ← Предыдущая страница | Следующая страница →