Взаимное расположение прямой на плоскости

P:A₁x+B₁y+C₁z+D₁=0^N₁{A₁,B₁}

Q:A₂x+B₂y+C₂z+D₂=0^N₂{A₂,B₂}

а)

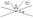
то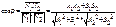

б)

p­­q<=> N₁||N₂, то A₁/A₂=B₁/B₂

в)

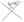p||q<=> N₁^N₂, то A₁A₂+B₁B₂=0

17. Общее ур-е прямой линии на плоскости. Его частные случаи.

Сначала запишем ур-е прямой, проходящей через заданную точку ^ заданному вектору.

M₀(x₀,y₀)

M₀M{x-x₀,y-y₀}

n*M₀M=0

A(x-x₀)+B(y-y₀)=0

Ax+By-Ax₀-By₀=0

-Ax₀-By₀=C

Ax+By+C=0-общее уравнение прямой на плоскости.

18.19. Каноническое ур-е прямой линии на плоскости. Ур-е прямой, проходящей ч/з 2 точки. Ур-е с угловым коэффициентом.

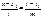
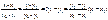
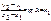
y-y₁=k₁(x-x₁)

y=k₁x-k₁x₁+y₁

y₁-k₁x₁=b

y=k₁x+b

ур-е прямой с угловым коэффициентом k.

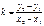
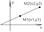Пусть даны 2 точки M₁(x₁,y₁), M₂(x₂,y₂) и x₁¹x₂, y₁¹y₂. Для составления уравнения прямой М₁М₂ запишем уравнения пучка прямых, проходящих через точку М₁: y-y₁=k(x-x₁). Т.к. М₂лежит на данной прямой, то чтобы выделить ее из пучка, подставим координаты точки М₂ в уравнение пучка М₁: y-y₁=k(x-x₁) и найдем k:

Теперь вид искомой прямой имеет вид:

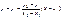или: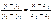

- Ур-е прямой, проходящей ч/з 2

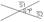20,21. Угол м/ду прямыми на плоскости. Условия || и^.

а)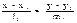

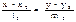
S₁{l₁,m₁} S₂{l₂,m₂},

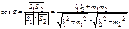
или

p:y=k₁x+b₁, k₁=tgj₁

q:y=k₂x+b₂, k₂=tgj₂ =>tgj=tg(j₂-j₁)=

=(tgj₂-tgj₁)/(1+ tgj₁tgj₂)=

=(k₂-k₁)/(1+k₁k₂).

б) p||q, tgj=0, k₁=k₂

в)p^q,то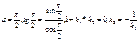

Расстояние от точки до прямой на плоскости и до плоскости в пространстве.

1. Ax+By+C=0, M₀(x₀,y₀)

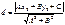
2. Пусть плоскость задана ур-ем Ax+By+Cz+D=0

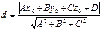
Кривые линии 2-го порядка.

Кривые 2го порядка описываются с помощью общего ур-я:

Ax²+2Bxy+Cy²+2Dx+2Ey+F=0, где

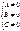
а) Каноническое ур-е эллипса

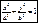- Каноническое ур-е эллипса

Если a=b, то x²+b²=a² - ур-е окружности.

б) Ур-е гиперболы: x²/a²-y²/b²=1

в) ур-е параболы: y²=2px или y=ax²

г) ур-е сферы: x²+y²+z²=а² (r²=(x-a)²+(y-b)²+(z-c)²)

д) ур-е эллипса: x²/a²-y²/b²+z²/c²=1

Парабола и ее свойства.

Множество точек плоскости, координаты которых по отношению к системе декартовых координат удовлетворяет уравнению y=ax², где х и у - текущие координаты, а- нек. число, наз. параболой.

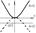Если вершина нах. в О(0,0), то ур-е примет вид

y²=2px-симметрично отн. оси ОХ

х²=2pу-симметрично отн. оси ОУ

Точка F(p/2,0) наз. фокусом параболы, а прямая x=-p/2 - ее директриса.

Любой точке М(х,у), принадлежащей параболе, расстояние до фокуса = r=p/2

Св-ва:

1. парабола предст. собой ¥ точек плоскости, равноотстающих от фокуса и от директрисы y=ax².

25.Эллипс и его св-ва:

Кривая второго порядка наз. эллипсом если коэффициенты А и L имеют одинаковые знаки

Аx²+Cy²=d

ур.-е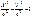

наз. канонич. ур.-ем эллипса, где 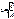При а=в представляет собой ур-е окружности х²+y²=а²

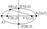
Точки F₁(-c,0) и F₂(c,0) - наз. фокусами эллипса а.

Отношение e=с/а наз. его эксцентриситетом (0<=e<=1)

Точки A₁,A₂,B₁,B₂ -вершины эллипса.

Св-во:
Для любой точки эллипса сумма расстояний этой точки до фокусов есть величина постоянной, =2а.

Гипербола и ее св-ва.

Кривая 2го порядка наз. гиперболой, если в ур-ии Ax²+Cy²=d, коэффициент А и С имеют противоположные знаки, т.е. А*С<0

б) Если d>0, то каноническое ур-е гиперболы примет вид: x²/a²-y²/b²=1, F1(c,o) и F₂(-c,0) - фокусы ее, e>0, e=c/a - эксцентриситет.

Св-во:
для любой точки гиперболы абсолютная величина разности ее расстояний до фокусов есть величина постоянная = 2а.

б) если d=0, ур-е примет вид x²/a²-y²/b²=0, получаем 2 перекрестные прямые х/а±у/b=0

в) если d<0, то x²/a²-y²/b²=-1 - ур-е сопряженной гиперболы.