Условия для магнитного поля на границе раздела двух изо-тропных сред (для самостоятельной работы)

Рассмотрим поведение линий индукции на границе двух веществ с разными магнитными проницаемостями. Предположим, что мы име-ем границу веществ, магнитные проницаемости которых обозначим через μ₁ и μ₂. Если мы возьмем малый участок S границы раздела, то его можно считать плоским, а поле вблизи него – с каждой стороны однородным. Значение вектора индукции в веществе с магнитной проницаемостью μ₁ обозначим через B₁, а в веществе с магнитной

проницаемостью μ₂ – через B₂ . Вблизи точек границы вектор магнит-ной индукции можно разложить на две составляющие, из которых од-на В_n будет перпендикулярна к границе раздела, а другая В_τ – парал-

лельна ей.
Тогда: B1	= B1n + B1τ , а B2	= B2 n + B2τ .
Установим	связь	между	нормальными составляющими векторов

магнитной индукции с двух сторон границы. Для этого рассмотрим поток магнитной индукции через замкнутую поверхность в виде ломаного ци-линдра, основания которого S₁ и S₂ равны и параллельны участку S границы, а образующие параллельны линиям индукции в тех веществах, в которых расположена данная часть цилиндра (рис. 4.6.1). Направим нор-маль n к границе раздела от первого вещества ко второму. Тогда для ос-нования S₂ это направление будет внешней нормалью, для основания S₁оно будет противоположно направлению внешней нормали.Согласно

теореме Гаусса ∫ Bn dS = 0 имеем: –B1n	S1+ B2n S2= 0.
S
S
B1		μ1
		μ2
n	B2	S

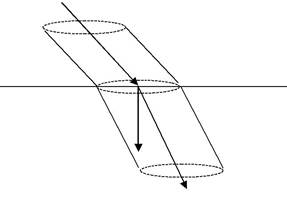
Рис.6.1.1

Знак минус получается вследствие того, что В_1n представляет со-бой проекцию B₁ на направление, противоположное направлению

внешней нормали к элементу поверхности S1. Замечая, что	S1= S2,
имеем: –B1n + B2n = 0, откуда
В1n= В2n.	(4.6.1)

Таким образом, нормальная составляющая вектора магнитной индукции не меняется при переходе из одного вещества в другое.

Определим соотношение между касательными составляющими векторов магнитной индукции H₁ и H₂ . В качестве контура, по кото-

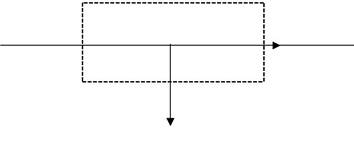
рому берется циркуляция вектора напряженности магнитного поля, выберем замкнутый контур аbсd (рис. 4.6.2), стороны аd и bс которого параллельны границе раздела веществ, а стороны аb и dс бесконечно малы. Так как на границе веществ предполагается отсутствие токов,

то согласно теореме о циркуляции вектора Н: _∫ Hdl = 0. Будем об-

abcda

ходить контур аbсdа по часовой стрелке и выберем за положительное направление касательной к границе раздела слева направо . Так как участки аb и dс предполагаются бесконечно малыми, то вся циркуля-ция выражается через участки bс и dа. Обозначая через Н₁ и Н₂ на-пряженности в обоих веществах соответственно, получаем:

H _1τbc − H _2τda =0.

b c

μ₁

τ μ2

a d

n

Рис. 4.6.2

Знак минус во втором члене получается вследствие того, что в нижней среде выбранное направление обхода противоположно поло-жительному направлению касательной. Учитывая, что bс = dа, имеем:

H1τ– H2τ= 0⇒ H1τ= H2τ.

(4.6.2)

Следовательно , касательная составляющая вектора напряжен-ности не меняется при переходе через границу раздела двух веществ.

Переходя к вектору магнитной индукции, в силу соотношения

B =μμ₀H,получим: ^B1τ=^μ1.

^B2τ ^μ2

Таким образом, касательные составляющие вектора магнитной индукции B с двух сторон границы веществ относятся, как магнит-

ные проницаемости μ этих веществ. В том случае, когда граница не перпендикулярна к линиям индукции, линии индукции претерпевают

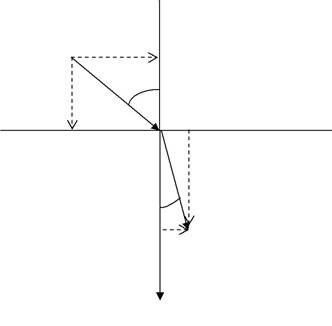
преломление. Разлагая векторы B₁ и B₂ на составляющие, параллель-ные границе и перпендикулярные к границе получим (рис. 4.6.3):

tgα1

B1τ

B1τB2 n

μ1

=

B1n

=

=

,

(4.6.3)

tgα

B2τ

B

B

μ

1n

2τ

^B2n

т. е. тангенсы угла наклона векторов индукции к нормали в двух ве-ществах относятся, как магнитные проницаемости веществ.

		B1τ
B1n	B	α1	μ1
			μ2

α₂

^B2n

B₂

^B2τ

n

Рис. 4.6.3

На законе преломления линий индукции основана магнитная защи-та. Она обусловлена тем, что благодаря преломлению линий индукции внутри полости, находящейся в веществе с большим значением магнит-ной проницаемости, магнитное поле оказывается близким к нулю.