Момент импульса и закон его сохранения

Моментом импульса (количеством движения) материальной точки A относительно неподвижной точки O называется физическая величина, определяемая векторным произведением:

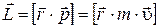
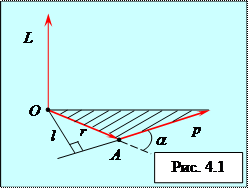
где r – радиус-вектор, проведённый из точки O в точку A; 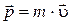– импульс материальной точки (рис. 4.1.); L – псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от r к p.

Модуль вектора момента импульса:

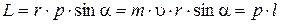
где a – угол между векторами r и p; l – плечо вектора p относительно точки O.

Моментом импульса материальной точки A относительно неподвижной оси Z называется скалярная величина L_z, равная проекции на эту ось вектора момента импульса. Значение момента импульса L_z не зависит от положения точки O на оси Z.

Проекцией момента импульса материальной точки называется:

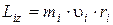
она направлена по оси в сторону, определяемую правилом правого винта.

Момент импульса твердого тела относительно оси есть сумма моментов импульсов отдельных материальных точек:

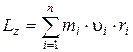
Используя формулу 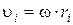, получим:

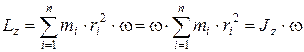
таким образом:

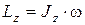
где J_z – момент инерции тела; w – угловая скорость.

Продифференцировав последнее уравнение по времени, получим:

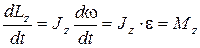
т.е. .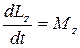

Это выражение - ещё одна форма уравнения (закона) динамики вращательного движения твёрдого тела относительно неподвижной оси.

В замкнутой системе вектор момента внешних сил M=0 и 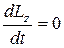, откуда:

.

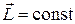Выражение представляет собой закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т.е. не меняется с течением времени.

Основная связь между величинами и уравнениями, определяющие вращение тела вокруг неподвижной оси и его поступательном движении:

№	Поступательное движение	Вращательное движение
1.	Масса	m	Момент инерции	J
2.	Скорость		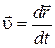Угловая скорость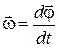
3.	Ускорение		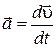Угловое ускорение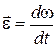
4.	Сила	F	Момент силы	Mz или M
5.	Импульс		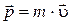Момент импульса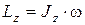
6.	Основное уравнение динамики		Основное уравнение динамики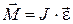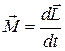
7.	Работа		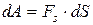Работа при вращательном движении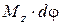
8.	Кинетическая энергия		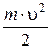Кинетическая энергия вращения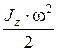

Деформации твердого тела

Рассматривая механику твердого тела, мы пользовались понятием абсолютно твердого тела. Однако в природе абсолютно твердых тел нет, так как все реальные тела под действием сил изменяют свою форму и размеры, т. е. деформируются.

Деформация– изменение форм и размеров тела.

Деформация называется упругой, если после прекращения действия внешних сил тело принимает первоначальные размеры и форму.

Деформации, которые сохраняются в теле после прекращения действия внешних сил, называются пластическими (или остаточными).

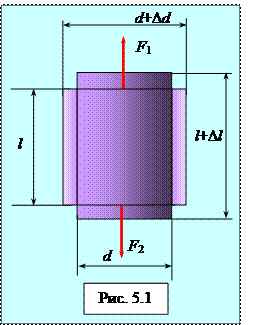Рассмотрим однородный стержень длиной l и площадью поперечного сечения S (рис, 1.1), к концам которого приложены направленные вдоль его оси силы F₁ и F₂(F₁=F₂=F), в результате чего длина стер­жня меняется на величину Dl.

Сила, действующая на единицу площади поперечного сечения, называется напряжением:

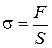(5.1)

Если сила направлена по нормали к по­верхности, напряжение называется нормальным, если же по касательной к поверхности — тангенциальным.

Количественной мерой, характеризую­щей степень деформации, испытываемой телом, является его относительная деформация. Так, относительное изменение длины стержня (продольная деформация)

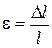(5.2)

относительное поперечное растяжение (сжатие)

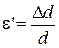
где d– диаметр стержня.

Деформации e иe'всегда имеют разные знаки (при растяжении Dlположительно, а Ddотрицательно, при сжатии Dlотрицательно, a Dd положительно).

Взаимосвязь e иe':

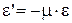
где m - положительный коэффициент, зависящий от свойств материала, называется коэффициент Пуассона.

Для малых деформаций относительное удлинение e и напряжение s прямо пропорциональны друг другу:

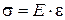(5.3)

где коэффициент пропорциональности Е называется модулем Юнга. Модуль Юнга определяется напряжением, вызывающим относительное удлинение, равное единице.

Из формул (5.2), (5.3) и (5-1) вытекает, что

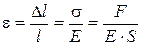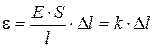или (5.4)

где k – коэффициент упругости.

Выражение (5.4) также задает закон Р. Гука (1635–1703 гг), согласно которому удлинение стержня при упругой деформации пропорционально действующей на стержень силе.

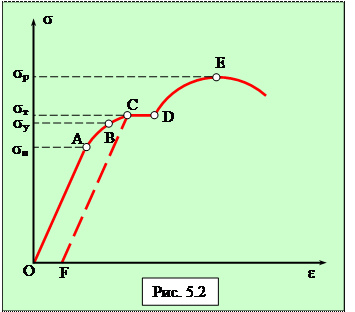Закон Гука, выполняется лишь на участке ОА, до предела пропорциональности(s_п). При дальнейшем увеличении напряжения деформация ещё упругая (хотя зависимость не линейна) и до предела упругости(s_у) остаточчые деформации не возникают.

За пределом упругости в теле возникают остаточные деформации и график, описывающий возвращение тела в первоначальное состояние после прекращения действия силы, изобразится не кривой ВО, апараллельной ей CF.

Напряжение, при котором появляется заметная остаточная деформация (»0,2%), называется пределом текучести(s_т) – точка С на кривой.

В области CD деформация возрастает без увеличения напряжения, т. е. тело как бы «течёт». Эта область называется областью текучести(или областью пластическихдеформаций).

Материалы, для которых область текучести значительна, называются вязкими,для которых же она практически отсутствует хрупкими.

При дальнейшем растяжении (за точку D) происходит разрушение тела. Максимальное напряжение, возникающее в теле до разрушения, называется пределом прочности(s_р).

Потенциальная энергия упруго растянутого (сжатого) стержня, равна работе, совершаемой внешними силами при деформации:

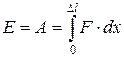
где х – абсолютное удлинение стержня, изменяющееся в процессе деформации от 0 до Dl. Согласно закону Гука (5.4),

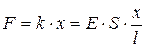
Поэтому

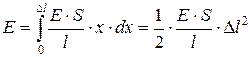
т.е. потенциальная энергия упругорастянутого стержня пропорциональна квадрату деформации Dl².

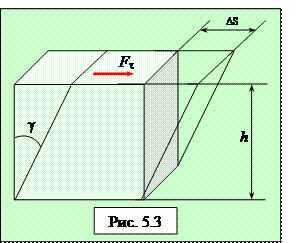Деформацию сдвига проще всего осуществить, если взять брусок, имеющий форму прямоугольного параллелепипеда, и приложить к нему силу F_t,(рис. 5.3), касательную к его поверхности (нижняя часть бруска закреплена неподвижно).

Относительная деформация сдвига определяется из формулы

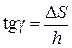
где DS – абсолютный сдвиг параллельных слоев тела относительно друг друга;

h – расстояние между слоями (для малых углов tgg»g).

ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ