Элементы векторной алгебры.
Скалярное, векторное, смешанное произведение.
Скалярное произведение 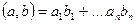 хорошо известно из школьного курса.
хорошо известно из школьного курса.
А сейчас мы научимся с помощью матриц и определителей находить общий перпендикуляр для пары векторов.
Векторное произведение.
Определение. Вектор 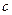 называется векторным произведением векторов называется векторным произведением векторов 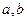 , обозначается , обозначается 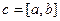 , если выполнены 3 условия: 1) , если выполнены 3 условия: 1) 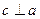 , , 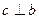 . 2) Векторы . 2) Векторы 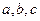 образуют правоориентированную тройку, то есть с конца вектора образуют правоориентированную тройку, то есть с конца вектора 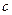 кратчайший поворот от кратчайший поворот от 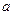 к к 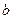 виден против часовой стрелки. 3) виден против часовой стрелки. 3) 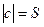 параллелограмма, образованного парой векторов параллелограмма, образованного парой векторов 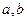 , то есть , то есть 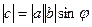 . . | 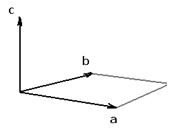 |
Таблица свойств скалярного и векторного произведений: сходство и различия.
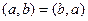 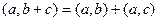 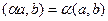 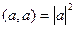 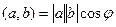 | 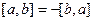 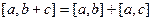 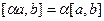 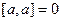 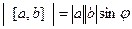 |
Метод нахождения векторного произведения с помощью определителя: Можно записать в 1-ю и 2-ю строку исходные два вектора, в третьей строке добавить произвольные обозначения осей 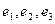 , и вычислить этот определитель.
, и вычислить этот определитель.
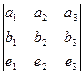 =
= 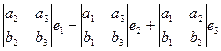 . Миноры порядка 2 вычислятся, эти числа как раз и будут координатами
. Миноры порядка 2 вычислятся, эти числа как раз и будут координатами 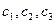 нового вектора, который является векторным произведением.
нового вектора, который является векторным произведением.
Пример. Найти векторное произведение векторов (1,1,1) и (1,2,3)
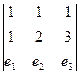 =
= 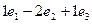 =
= 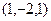 . Ответ (1,-2,1).
. Ответ (1,-2,1).
Также можно проверить, что он действительно перпендикулярен исходным векторам (скалярно умножить на 1-й или на 2-й вектор, получим 0).
Примечание. Определитель можно вычислять либо разложением по 3-й строке, либо ранее известными методами, в том числе добавить копии двух первых столбцов справа.
Смешанное произведение. Определеятся так: 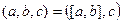 .
.
Этот объект корректно определён и существует: векторное произведение первой пары есть какой-то вектор, и его можно скалярно умножить на ещё один, третий вектор, в итоге получится константа.
Смешанное произведение вычисляется с помощью определителя так: 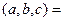
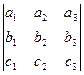 .
.
Обоснование: Если рассмотреть разложение этого определителя по третьей строке, то получится
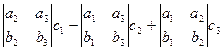 , то есть 1-я координата векторного произведения
, то есть 1-я координата векторного произведения 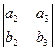 как раз и умножается на 1-ю координату вектора
как раз и умножается на 1-ю координату вектора 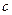 , 2-я на 2-ю и т.д. то есть это и есть
, 2-я на 2-ю и т.д. то есть это и есть 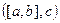 .
.
Геометрический смысл: объём параллелепипеда, образованного тремя векторами.
Глава 2. Системы линейных уравнений.
Введение, основные методы решения.
Произвольная система
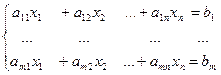
система из m линейных уравнений с m неизвестными.
Примечание. Не обязательно все n переменных есть в каждом уравнении, в некоторых какие-то могут быть пропущены, то есть коэффициенты 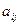 = 0.
= 0.
Уравнения здесь называются линейными потому, что все неизвестные именно в первой степени, то есть нигде не возводятся в квадрат, не умножаются между собой, не извлекается корень и т.д.
Если при этом ещё и все 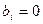 , то система называется однородной.
, то система называется однородной.
Решением системыназывается такой набор констант 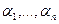 , что при подстановке их вместо
, что при подстановке их вместо 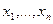 во всех уравнениях получатся тождества. Можно представлять также и в виде вектора
во всех уравнениях получатся тождества. Можно представлять также и в виде вектора 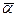 .
.
Обычный, матричный и векторный виды записи системы уравнений:
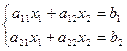 ,
, 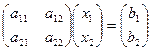 ,
,
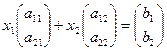 .
.
Основная (А) и расширенная матрица (С).
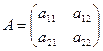 ,
, 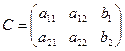 .
.
Определение. Если существует хотя бы одно решение (то есть набор 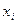 , обращающий в тождества все уравнения) то система называется совместной, а если решения не существует, то несовместной, или противоречивой.
, обращающий в тождества все уравнения) то система называется совместной, а если решения не существует, то несовместной, или противоречивой.
Слово «совместная» система означает, что уравнения совместны между собой, не противоречат друг другу. Примеры:
Совместная: 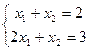 есть решение (1,1).
есть решение (1,1).
Несовместная 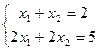 если вычесть из 2-го уравнения удвоенное первое, получим противоречие: 0=1.
если вычесть из 2-го уравнения удвоенное первое, получим противоречие: 0=1.
Если в правой части 2-го уравнения было бы 4, а не 5, то система была бы совместной.
ЛЕКЦИЯ № 4. 23.09.2016
Теорема Кронекера-Капелли о совместности системы уравнений.
Система линейных уравнений совмстна тогда и только тогда, когда 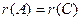 (ранг основной матрицы равен рангу расширенной матрицы).
(ранг основной матрицы равен рангу расширенной матрицы).
Замечание. Вообще, при добавлении нового столбца ранг может или остаться прежним, или увеличиться на 1.
Идея доказательства. Если вектор 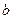 (вспомним векторный вид системы) является линейной комбинацией столбцов матрицы А, то существуют
(вспомним векторный вид системы) является линейной комбинацией столбцов матрицы А, то существуют 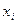 - коэффициенты, и решение существует, а если он не является линейной комбинацией столбцов матрицы А, то
- коэффициенты, и решение существует, а если он не является линейной комбинацией столбцов матрицы А, то 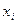 не существует, и решения нет.
не существует, и решения нет.
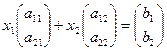 или
или 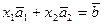 .
.
Рассмотрим расширенную матрицу для системы из недавнего примера:
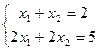 ,
, 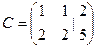
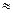
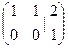 . Если рассматривать основную матрицу (до черты) там ранг = 1, потому что во 2-й строке только нули. А если всю расширенную матрицу, то там есть невырожденный минор 2-го порядка:
. Если рассматривать основную матрицу (до черты) там ранг = 1, потому что во 2-й строке только нули. А если всю расширенную матрицу, то там есть невырожденный минор 2-го порядка: 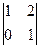 . Ранги основной и расширенной матриц не совпадают.
. Ранги основной и расширенной матриц не совпадают.
