Упражнения для самостоятельной работы
 3х + (20 – х) = 35,2,
3х + (20 – х) = 35,2,

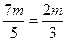 ,
, 
 (х – 3)
(х – 3)  - х
- х 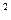 = 7 – 5х.
= 7 – 5х.
 (х + 2)
(х + 2) 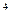 - 11(х + 2)
- 11(х + 2) 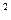
 = 12.
= 12.
 х
х 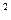 = х
= х 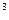 ,
,
 3у
3у 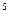 = 96,
= 96,
 х
х 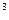 + х
+ х 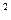 + х + 1 = 0,
+ х + 1 = 0,
 – 5,5n(n – 1)(n + 2,5)(n -
– 5,5n(n – 1)(n + 2,5)(n - 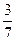 ) =0.
) =0.

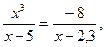 а)2 +
а)2 + 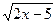 =4,
=4,

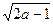 =-5,
=-5,

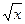 = - x. а)
= - x. а) 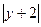 =
= 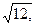
 2а
2а 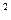 х – 5 = 17.
х – 5 = 17.
 х
х 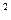 + 2х - 15=0;
+ 2х - 15=0;
 (х
(х 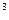 - 4х)
- 4х) 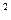 - 7(х
- 7(х 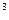 - 4х) +12=0;
- 4х) +12=0;
 х
х 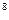 +9х
+9х 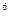
 - х
- х 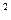 -9=0;
-9=0;
 у
у 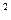 -15
-15 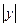 =0;
=0;
 х
х 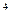 - 625=0.
- 625=0.
Список литературы
25.Пехлецкий И. Д. Математика, СПО. - М.: Академия, 2008.
26. Григорьев С.Г., Задулина С.В. Математика, СПО. - М.: Академия, 2009.
27. Спирина М.С., Спирин П.А. Теория вероятностей и математическая статистика, СПО. - М.: Академия, 2007.
28. Валуце И.И., Дилигул Г.Д. Математика для техникумов. - М.: Наука, 1980.
29. Подольский В. А., Суходский А.М. Сборник задач по высшей математике. - М.: Высшая школа, 1974.
30. Башмаков М.И. Математика, 10 кл. - М.: Академия, 2009.
31. Башмаков М.И. Математика, 11 кл. - М.: Академия, 2009.
32. Шибасов Л.П., Шибасова З.Ф. За страницами учебника математики. - М.: Просвещение, 1997.
ПРАКТИЧЕСКАЯ РАБОТА № 7
«Производная»
Цели урока:
1) Обобщить теоретические знания по теме: «Производная».
2) Рассмотреть алгоритмы решений заданий теме « Производная» , решить задачи самостоятельной работы с использованием геометрического и механического смысла производной .
3) Формировать ответственность; самоконтроль, рассудительность.
Теоретический материал
Ход работы:
Используя определения теории дифференциалов, представленные ниже выполните задания своего варианта.
1.Производнойфункции 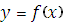 в данной точке
в данной точке 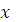 называют предел отношения приращения функции ∆y к соответствующему приращению аргумента ∆x при условии, что ∆x→0, т.е.
называют предел отношения приращения функции ∆y к соответствующему приращению аргумента ∆x при условии, что ∆x→0, т.е.
2 Геометрическая интерпретация производной, , состоит в следующем: значение производной функции 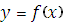 в точке x равно угловому коэффициенту касательной, проведённой к графику функции в той же точке x,т.е.
в точке x равно угловому коэффициенту касательной, проведённой к графику функции в той же точке x,т.е. 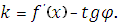
Уравнение касательной, как всякой прямой, проходящей через данную точку в данном направлении, имеет вид 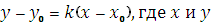 – текущие координаты. Но
– текущие координаты. Но 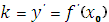 и уравнение касательной запишется так:
и уравнение касательной запишется так: 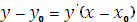 . Уравнение нормали запишется в виде
. Уравнение нормали запишется в виде 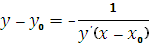 .
.

 3. Механическое истолкование производной заключается в следующем: скорость движения материальной точки в данный момент времени равна производной пути по времени, т.е.
3. Механическое истолкование производной заключается в следующем: скорость движения материальной точки в данный момент времени равна производной пути по времени, т.е. 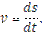
Вариант № 1 1.Напишите уравнение касательной, проведенной к графику функции у = х²+2x через точку с абсциссой х = 3. 2.Тело движется по прямой и при этом его координата меняется в зависимости от времени по закону х = 3t4+ 5t + 6 (м).Найдите скорость тела и его ускорение в момент t = 7с. 3.Составьте и решите неравенство 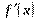 > 0 , если > 0 , если 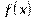 = = 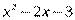 | Вариант №2 1.К графику функции y = f(x) = x²+ 6x +7 проведена касательная через точку с абсциссой х = -1. Найдите угловой коэффициент касательной. 2.Тело движется по прямой и при этом его координата меняется в зависимости от времени по закону х = 2t3+ 3t2 + 4 (м).Найдите скорость тела и его ускорение в момент t = 2с. 3. Составьте и решите неравенство 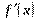 > 0 , если > 0 , если 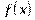 = = 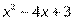 | Вариант №3 1.Маховик вращается и точки его поверхности движутся по закону j(t)=t +6t²+12t(рад). Найдите угловую скорость и угловое ускорение точек в момент t = 1с. 2.К графику функции y = f(x) = 3x4+ 8x +9 проведена касательная через точку с абсциссой х = -1. Найдите угловой коэффициент касательной. 3. Составьте и решите неравенство 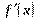 > 0 , если > 0 , если 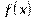 = = 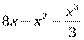 |
Список литературы
33.Пехлецкий И. Д. Математика, СПО. - М.: Академия, 2008.
34. Григорьев С.Г., Задулина С.В. Математика, СПО. - М.: Академия, 2009.
35. Спирина М.С., Спирин П.А. Теория вероятностей и математическая статистика, СПО. - М.: Академия, 2007.
36. Валуце И.И., Дилигул Г.Д. Математика для техникумов. - М.: Наука, 1980.
37. Подольский В. А., Суходский А.М. Сборник задач по высшей математике. - М.: Высшая школа, 1974.
38. Башмаков М.И. Математика, 10 кл. - М.: Академия, 2009.
39. Башмаков М.И. Математика, 11 кл. - М.: Академия, 2009.
40. Шибасов Л.П., Шибасова З.Ф. За страницами учебника математики. - М.: Просвещение, 1997.
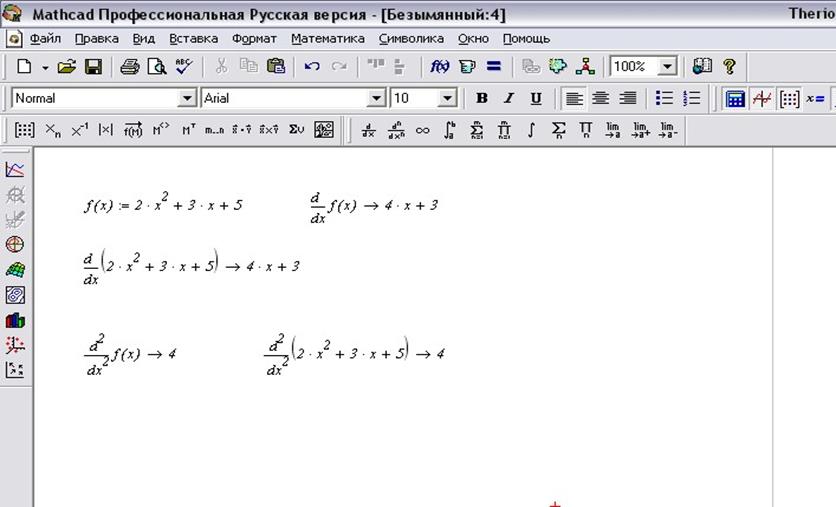
ПРАКТИЧЕСКАЯ РАБОТА № 9
«Нахождение производных в среде Mathcad»
Цели урока:
1) Обобщить теоретические знания по теме: «Нахождение производных функций в среде Mathcad».
2) Рассмотреть алгоритмы решений заданий по данной теме, используя формулы вероятности событий, решить задачи.
3) Формировать умение планировать свою деятельность, умение ставить цели и реализовывать их.
Теоретический материал