Тема 11. Определённый интеграл. Несобственные интегралы.

Определённый интеграл, условия его существования, геометрический смысл и свойства. Формула Ньютона-Лейбница. Формулы замены переменной и интегрирования по частям в определённом интеграле. Геометрические приложения определённого интеграла. Несобственные интегралы по бесконечному промежутку интегрирования и от неограниченных функций.

Литература: [2]–C.278-318; [5] – C.177-212.

Раздел IV. Дифференциальные уравнения.

Тема 12. Дифференциальные уравнения первого порядка.

Понятие дифференциального уравнения (ДУ). ДУ 1-ого порядка: основные понятия и определения (формы записи, решение, начальное условие, общее и частное решения). Задача Коши. Основные типы ДУ 1-ого порядка: с разделёнными и разделяющимися переменными, однородное, линейное, Бернулли.

Литература: [2]–C.319-334; [5] –C.416-423.

Тема 13. Дифференциальные уравнения высших порядков.

ДУ порядка 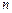: основные понятия и определения (формы записи, решение, начальные условия, общее и частное решения). Задача Коши. ДУ допускающие понижение порядка. Линейные ДУ второго порядка с постоянными коэффициентами, нахождение их решений.

Литература: [2]–C.334-342 [5]–C.431-449.

Раздел V. Теория вероятностей и математическая статистика.

Тема 14. Случайные события и их вероятности.

Случайные события, действия над ними. Виды событий. Вероятность события, её определения. Правила и формулы комбинаторики, вычисление вероятностей с их помощью. Формулы сложения и умножения вероятностей, полной вероятности и Байеса, Бернулли, вычисление вероятностей с их помощью.

Литература: [1]–C.17-56;[3]–C.16-70.

Тема 15. Случайные величины.

Понятие случайной величины. Дискретная и непрерывная случайные величины, способы их задания и числовые характеристики. Основные законы распределения случайных величин, их числовые характеристики.

Литература:[1]–C.64-155; [3]–C.86-174.

Тема 16. Элементы математической статистики. Предварительная обработка статистических данных.

Понятия генеральной совокупности и выборки. Основные способы записи выборки: вариационный ряд; дискретный и интервальный статистические ряды. Числовые характеристики выборки и её графическое изображение (полигон, гистограмма).

Литература: [1]–C.187-207; 234-235; [3]–C.264-285.

Рекомендуемая литература.

Основная литература:

1. Гмурман В.Е. Теория вероятностей и математическая статистика: Учеб. пособие для студентов вузов. –М.: Высш.шк., 2005.

2. Кремер Н.Ш., Путко Б.А., Тришин И.М., Фридман М.Н. Высшая математика для экономистов. Учеб. пособие для вузов. -М.: ЮНИТИ-ДАНА, 2000.

3. Кремер Н.Ш. Теория вероятностей и математическая статистика: Учебник для вузов. –М.: ЮНИТИ-ДАНА, 2004.

4. Шипачев В.С. Высшая математика. Учебник для вузов. -М.: Высшая школа, 2002.

5. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учеб. Пособие для студентов вузов. –М.: Высш.шк., 2003.

6. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2-х частях. Часть 1, 2. Учеб. пособие для втузов. –М.: Высшая школа, 1997.

Дополнительная литература:

7. Ахтямов А.М. Математика для социологов и экономистов: Учеб. пособие. –М.: ФИЗМАТЛИТ, 2006.

8. Дорофеева А.В. Высшая математика. Гуманитарные специальности: Учеб. пособие для вузов. – М.: Дрофа, 2004.

9. Красс М.С. Математика для экономических специальностей. Учебник. –М.: Дело, 2003.

10. Общий курс высшей математики для экономистов. Учебник /Под ред. В.И.Ермакова. М.:ИНФРА-М, 1999.

11. Клименко Ю.И. Высшая математика для экономистов в примерах и задачах. Учебник. -М.: ЭКЗАМЕН, 2006.

12. Практикум по высшей математике для экономистов: Учеб. пособие для вузов/ Кремер Н.Ш., Тришин И.М., Путко Б.А. и др. Под ред. проф. Н.Ш.Кремера. –М.: ЮНИТИ-ДАНА, 2002.

13. Сборник задач по математике для вузов. Под ред. Котляра Л.М., Углова А.Н. -Наб. Челны: Изд-во ИНЭКА, 2006,2007.