Модель обслуживания машинного парка

Модель обслуживания машинного парка представляет собой модель замкнутой системы массового обслуживания: интенсивность l входящего потока заявок зависит от состояния системы, причем источник требований является внутренним и генерирует ограниченный поток заявок.

Пусть машинный парк состоит из N машин и обслуживается бригадой R техников (N > R), причем каждая машина может обслуживаться только одним техником. Здесь машины являются источниками требований (заявок на обслуживание), а техники – обслуживающими каналами. Интенсивность зависит от того, сколько машин в данный момент находится в эксплуатации (N – k) и сколько машин обслуживается или стоит в очереди, ожидая обслуживания (k). Общий (суммарный) входящий поток имеет интенсивность (N – k)l.

Требование, поступившее в систему в момент, когда свободен хотя бы один канал, немедленно идет на обслуживание. Если требование застает все каналы занятыми обслуживанием других требований, то оно не покидает систему, а становится в очередь и ждет, пока один из каналов не станет свободным. Таким образом, в замкнутой системе массового обслуживания входящий поток требований формируется из выходящего.

Состояние S_k системы характеризуется общим числом требований, находящихся на обслуживании и в очереди, равным k. Для рассматриваемой замкнутой системы, очевидно, k = 0, 1, 2, ..., N. При этом если система находится в состоянии S_k, то число объектов, находящихся в эксплуатации, равно (N – k).

Если l – интенсивность потока требований в расчете на одну машину, то:

;

.

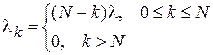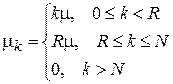Система алгебраических уравнений, описывающих работу замкнутой СМО в стационарном режиме, выглядит следующим образом (y = l/m):

,

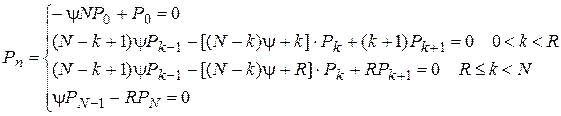Решая данную систему, находим вероятность k-гo состояния:

.

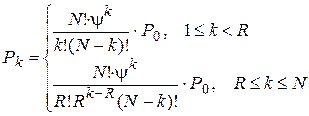Величина P₀ определяется из условия нормирования 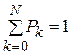полученных результатов по формулам для P_k, k = 0, 1, 2, ..., N. Определим следующие вероятностные характеристики системы:

- среднее число требований в очереди на обслуживание:

;

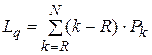- среднее число требований, находящихся в системе (на обслуживании и в очереди):

;

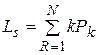- среднее число техников (каналов), простаивающих из-за отсутствия работы:

;

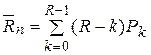- коэффициент простоя обслуживаемого объекта (машины) в очереди:

;

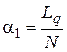- коэффициент использования объектов (машин):

;

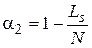- коэффициент простоя обслуживающих каналов (техников):

;

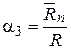- среднее время ожидания обслуживания (время ожидания обслуживания в очереди):

.

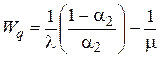5. Сетевые модели (N-схемы). Сети Петри

5.1. Теоретические основы сетей Петри: принципы построения, алгоритмы поведения

Сети Петри были разработаны и используются для моделирования систем, которые содержат взаимодействующие параллельные компоненты, например аппаратное и программное обеспечение ЭВМ, гибкие производственные системы, а также социальные и биологические системы.

Введение в теорию комплектов

Математическим аппаратом сетей Петри является теория комплектов (естественное расширение теории множеств). Как и множество, комплект является набором элементов из некоторой области. В отличие от множества, где элемент либо является элементом множества, либо нет, в комплект элемент может входить заданное число раз.

Основным понятием теории комплектов является функция числа экземпляров: #(x, B) – число x в B, т.е. число экземпляров элемента x в B.

Элемент х является членом комплекта B, если #(x, B) > 0. Аналогично, если #(x, B) = 0, то х не принадлежит B. Æ – пустой комплект, не имеющий членов (для всех х: #(x, 0) = 0). Если ограничить число элементов в комплекте так, что 0 £ #(x, B) £ 1, то получим теорию множеств.

Под мощностью |B| комплекта B понимается общее число экземпляров в комплекте |B| = S_x#(x, B).

Комплект A является подкомплектом комплекта B, если каждый элемент A является элементом B, по крайней мере, не большее число раз, т.е. A Í B тогда и только тогда, когда #(x, A) £ #(x, B) для всех х.

Два комплекта равны (А = В), если #(x, A) = #(x, B).

Комплект A строго включен в комплект B (A Ì B), если A Í B и A ¹ B. Над комплектами определены 4 операции:

- объединение A È B: #(x, A È B) = max(#(x, A), #(x, B));

- пересечение A Ç B: #(x, A Ç B) = min(#(x, A), #(x, B));

- сумма A + B: #(x, A + B) = #(x, A) + #(x, B);

- разность A – B: #(x, A – B) = #(x, A) – #(x, B).

Назовем множество элементов, из которых составляются комплекты, областью D. Пространство комплектов Dⁿ есть множество всех таких комплектов, что элементы их принадлежат D и ни один из элементов не входит в комплект более n раз. Иначе говоря, для любого B Î Dⁿ:

- из x Î B следует х Î D;

- для любого х #(x, B) £ n.

Множество D^¥ есть множество всех комплектов над областью D без какого-либо ограничения на число экземпляров элемента в комплекте.

Структура сети Петри

Сеть Петри состоит из 4 компонентов C = (P, T, I, O), которые и определяют ее структуру:

- конечное множество позиций P = {p₁, p₂, ..., p_n}, n ³ 0 – мощность множества P;

- конечное множество переходов T = {t₁, t₂, ..., t_m}, m ³ 0 – мощность множества T;

- входная функция I: T ® P^¥ – отображение из переходов в комплекты позиций;

- выходная функция O: T ® P^¥ – отображение из переходов в комплекты позиций.

Входная и выходная функции связаны с переходами и позициями. Входная функция I отображает переход t_j во множество позиций I(t_j), называемых входными позициями перехода. Выходная функция O отображает переход t_j во множество позиций O(t_j), называемых выходными позициями перехода. Множества позиций и переходов не пересекаются.

Позиция p_i является входной позицией перехода t_j в том случае, если p_i Î I(t_j); p_i является выходной позицией перехода, если p_i Î O(t_j).

Входы и выходы переходов представляют комплекты позиций. Кратность входной позиции для перехода t_j есть число появлений позиции во входном комплекте перехода #(p_i, I(t_j)). Аналогично, кратность выходной позиции p_i для перехода t_j есть число появлений позиции в выходном комплекте перехода #(p_i, O(t_j)).

Переход t_j есть выход позиции p_i, если p_i есть вход t_j (рис. 5.1). Переход t_j является входом позиции p_i, если p_i есть выход t_j (рис. 5.2).

Рис. 5.1	Рис. 5.2

Определим расширенную входную функцию I и выходную функцию O таким образом, что #(t_j, I(p_i)) = #(p_i, O(t_j)); #(t_j, O(p_i)) = #(p_i, I(t_j)).

Графы сетей Петри

Теоретико-графовым представлением сети Петри является двудольный ориентированный мультиграф G = (V, A), где

V = {v₁, v₂, ..., v_s} – множество вершин;

А = {a₁, a₂, ..., a_r} – комплект направленных дуг a_i = {v_j, v_k}, где v_j, v_k Î V.

Множество V может быть разбито на два непересекающихся подмножества P и T (P Ç T = 0), и если a_i = (v_j, v_k), тогда либо v_j Î P и v_k Î T, либо v_j Î T и v_k Î P.

Сеть Петри есть ориентированный мультиграф, т.к. он допускает существование направленных кратных дуг от одной вершины к другой. Граф является двудольным, т.к. он допускает существование вершин двух типов: позиций (кружок O) и переходов (планка |).

Ориентированные дуги соединяют позиции и переходы. Дуга, направленная от позиции p_i к переходу t_j, определяет позицию, которая является входом перехода t_j. Кратные входы в переход указываются кратными дугами из входных позиций в переход. Выходная позиция указывается дугой от перехода к позиции. Кратные выходы также представлены кратными дугами.

Пример. Пусть задана следующая структура сети Петри: C = (P, T, I, O), n = 6, m = 5 (рис. 5.3).

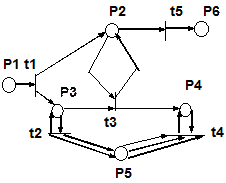
Рис. 5.3

P = {p₁, p₂, p₃, p₄, p₅, p₆} T = {t₁, t₂, t₃, t₄, t₅}

I(t₁) = {p₁} O(t₁) = {p₂, p₃}

I(t₂) = {p₃} O(t₂) = {p₃, p₅, p₅}

I(t₃) = {p₂, p₃} O(t₃) = {p₂, p₄}

I(t₄) = {p₄, p₅, p₅, p₅} O(t₄) = {p₄}

I(t₅) = {p₂} O(t₅) = {p₆}

Расширенными входной и выходной функциями являются:

I(p₁) = {} O(p₁) = {t₁}

I(p₂) = {t₁, t₃} O(p₂) = {t₃, t₅}

I(p₃) = {t₁, t₂} O(p₃) = {t₂, t₃}

I(p₄) = {t₃, t₄} O(p₄) = {t₄}

I(p₅) = {t₂, t₂} O(p₅) = {t₄, t₄, t₄}

I(p₆) = {t₅} O(p₆) = {}

Оба представления сети Петри – в виде структуры и в виде графа – эквивалентны. Их можно преобразовать друг в друга.

Маркировка сетей Петри

Маркировка m есть присвоение фишек позициям сети Петри. Фишка – это одна из компонент сети Петри (подобно позициям и переходам). Фишки присваиваются позициям. Их количество при выполнении сети может изменяться. Фишки используются для отображения динамики системы.

Маркированная сеть Петри есть совокупность структуры сети Петри C = (P, T, I, O) и маркировки m и может быть записана в виде M = (P, T, I, O, m). На графе сети Петри фишки изображаются крупными точками в кружке, который представляет позицию сети Петри. Количество фишек (точек) для каждой позиции не ограничено и, следовательно, в целом для сети существует бесконечно много маркировок. Множество всех маркировок сети, имеющей n позиций, является множеством всех n векторов, т.е. Nⁿ. Очевидно, что хотя это множество и бесконечно, но оно счетно. Когда маркировка превышает 4 или 5 фишек, то в кружках не рисуют фишки, а указывают их количество (рис. 5.4).

Структура сети Петри может оставаться неизменной, а маркировка сети может меняться.

Пример: Маркировка m = (12, 22, 8, 10), m¢ = (13, 22, 9, 10).