Классы интегрируемых функций 5 страница
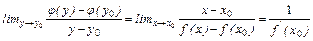 .
.
Здесь, очевидно, имеется в виду, что 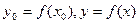 .Теорема доказана.
.Теорема доказана.
Она позволяет не вычислять отдельно производные обратных функций, если производные прямых функций известны.
7. Выпуклые функции
Мы будем рассматривать функции, заданные на промежутках числовой оси. Пусть 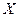 - такой промежуток.
- такой промежуток.
Определение 7.1.Функция  называется выпуклой на множестве
называется выпуклой на множестве 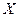 , если для любого
, если для любого 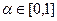 и для любых точек
и для любых точек 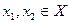 имеет место неравенство
имеет место неравенство
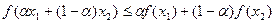 .
.
Эквивалентное определение:  выпуклая, если для любых
выпуклая, если для любых 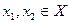 и любых
и любых 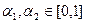 , таких, что
, таких, что 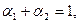 выполняется неравенство
выполняется неравенство
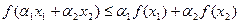 .
.
Функция называется строго выпуклой, если для всех 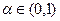 выполняется строгое неравенство. Функция называется вогнутой, если неравенство выполняется с противоположным знаком.
выполняется строгое неравенство. Функция называется вогнутой, если неравенство выполняется с противоположным знаком.
Понятно, что если  - выпуклая, то
- выпуклая, то 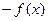 - вогнутая (и наоборот).
- вогнутая (и наоборот).
Геометрически функция является выпуклой, если хорда, соединяющая любые две точки её графика, лежит выше самого графика. Будем считать в дальнейшем 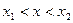 .
.
Полагая 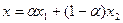 , получим
, получим
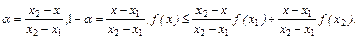

Последнее неравенство эквивалентно такому
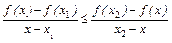 ,
,
в чём легко убедиться, освободившись от знаменателей. Это неравенство назовём основным.
Геометрически основное неравенство показывает, что при 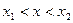 тангенс угла наклона хорды слева (от
тангенс угла наклона хорды слева (от 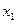 к
к 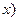 всегда не превосходит тангенса угла наклона хорды справа (от
всегда не превосходит тангенса угла наклона хорды справа (от  к
к  ); иными словами, тангенс угла наклона хорды не убывает при движении от точки
); иными словами, тангенс угла наклона хорды не убывает при движении от точки  к точке
к точке 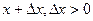 .
.
Теорема 7.1.Если  - выпуклая функция на промежутке
- выпуклая функция на промежутке 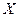 и
и  - внутренняя точка
- внутренняя точка 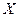 , то
, то 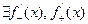 (конечные!).
(конечные!).
Доказательство. В неравенстве
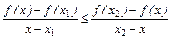 устремим
устремим 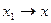 . Поскольку левая часть не убывает и ограничена, у неё есть предел, который по определению совпадает с
. Поскольку левая часть не убывает и ограничена, у неё есть предел, который по определению совпадает с 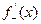 . Аналогично, устремив
. Аналогично, устремив 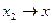 в том же неравенстве, получим, что
в том же неравенстве, получим, что 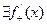 .
.
Теорема доказана.
Следствие 7.1. Выпуклая функция непрерывна в любой внутренней точке области определения.
Действительно, из существования правой и левой производных следует, что 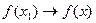 и
и 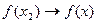 при
при 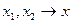 .
.
Теорема 7.2.Для того, чтобы дифференцируемая функция  была выпуклой на промежутке
была выпуклой на промежутке 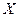 , необходимо и достаточно, чтобы её первая производная не убывала.
, необходимо и достаточно, чтобы её первая производная не убывала.
Доказательство. Если функция выпуклая, то устремляя  в основном неравенстве сначала к
в основном неравенстве сначала к 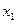 , а потом к
, а потом к  , получим
, получим 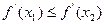 .
.
Наоборот, если выполнено неравенство 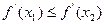 , пусть
, пусть 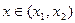 .Если на всём
.Если на всём 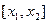 производная равна константе, то основное неравенство выполняется. Если производные не равны, то ,по теореме Лагранжа, имеем
производная равна константе, то основное неравенство выполняется. Если производные не равны, то ,по теореме Лагранжа, имеем
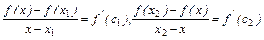 , где
, где 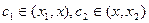 . По предположению,
. По предположению, 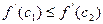 , и мы получили основное неравенство. Теорема доказана.
, и мы получили основное неравенство. Теорема доказана.
Теорема 7.3. Для того, чтобы функция была строго выпуклой на промежутке, достаточно, чтобы её производная строго возрастала.
Для доказательства следует только обратить внимание на то, что в предыдущем доказательстве, в условиях теоремы 7.2, всегда будет 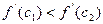 .
.
Теорема 7.4. Для того, чтобы дважды дифференцируемая на промежутке функция была выпуклой, необходимо и достаточно, чтобы её вторая производная была неотрицательной.
Очевидно, так как условие означает, что производная первая не убывает.
Теорема 7.5.Для того, чтобы дважды дифференцируемая функция была строго выпуклой, достаточно, чтобы её вторая производная была положительной.
В этом случае первая производная строго возрастает.
Теорема 7.6. Для того, чтобы функция 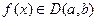 была выпуклой, необходимо и достаточно, чтобы в любой точке
была выпуклой, необходимо и достаточно, чтобы в любой точке 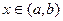 её график лежал не ниже касательной.
её график лежал не ниже касательной.
Доказательство. Если функция в точке  лежит выше касательной, то имеет место неравенство
лежит выше касательной, то имеет место неравенство
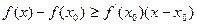 .Если
.Если 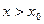 , оно означает, что
, оно означает, что 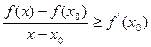 , если
, если 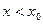 , неравенство будет в обратную сторону. То есть, для любых
, неравенство будет в обратную сторону. То есть, для любых 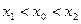 будет
будет 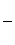
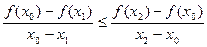 - основное неравенство. Значит, функция выпуклая.
- основное неравенство. Значит, функция выпуклая.
Наоборот, если функция выпуклая, то для любых 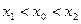 выполняется неравенство
выполняется неравенство
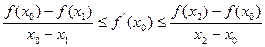 , которое эквивалентно утверждению, что функция лежит выше касательной. Теорема доказана.
, которое эквивалентно утверждению, что функция лежит выше касательной. Теорема доказана.
8. Дополнительные сведения о свойствах дифференцируемых функций
Теорема 8.1. (Дарбу). Пусть 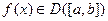 . Если
. Если 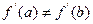 , то
, то 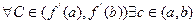 , для которой
, для которой 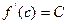 .
.
Доказательство. Положим 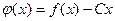 . Тогда
. Тогда 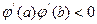 . Пусть, для определённости,
. Пусть, для определённости, 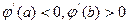 . Тогда
. Тогда 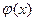 правее точки
правее точки 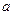 убывает, левее точки
убывает, левее точки 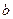 - возрастает. Значит, минимум функции
- возрастает. Значит, минимум функции 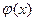 достигается внутри интервала
достигается внутри интервала 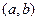 в некоторой точке
в некоторой точке 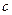 . Очевидно, функция
. Очевидно, функция 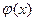 дифференцируема в точке
дифференцируема в точке 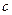 и некоторой её окрестности. Следовательно,
и некоторой её окрестности. Следовательно, 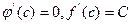 и теорема доказана.
и теорема доказана.
Таким образом, для производных верен аналог теоремы Коши для непрерывных функций.
Рассмотрим теперь вопрос о непрерывности прозводной.
Из теоремы Лагранжа следует, что 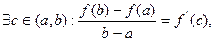 если
если 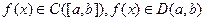 . Пусть при этих предположениях
. Пусть при этих предположениях 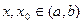 . Тогда
. Тогда
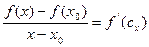 . Пусть
. Пусть 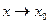 .Тогда
.Тогда 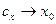 .Выражение слева будет стремиться к
.Выражение слева будет стремиться к 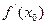 , и предел правого выражения тоже будет равен
, и предел правого выражения тоже будет равен 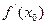 . Предел
. Предел 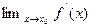 может при этом существовать, в этом случае производная будет непрерывна в точке
может при этом существовать, в этом случае производная будет непрерывна в точке  .Но он может и не существовать, как показывает пример функции
.Но он может и не существовать, как показывает пример функции 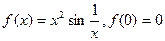 .Таким образом, верна
.Таким образом, верна
Теорема 8.2. (о разрывах производных). Если функция 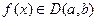 , то в любой точке этого интервала её производная либо непрерывна, либо имеет разрыв второго рода (в разных точках по-разному).
, то в любой точке этого интервала её производная либо непрерывна, либо имеет разрыв второго рода (в разных точках по-разному).
Второй семестр
ИНТЕГРАЛЫ
1.Неопределённый интеграл и первообразная
Определение 1.1. Пусть функция  определена на отрезке
определена на отрезке 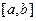 .Функция
.Функция 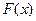 называется первообразной для функции
называется первообразной для функции  на отрезке
на отрезке 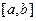 , если
, если 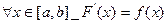 . Вместо отрезка
. Вместо отрезка 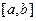 можно взять любой промежуток
можно взять любой промежуток 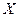 .
.
Пусть 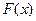 - первообразная для
- первообразная для  на
на 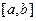 . Тогда и
. Тогда и 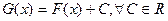 , будет первообразной для
, будет первообразной для  на том же отрезке.
на том же отрезке.
Пусть теперь 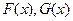 - две любых первообразных для
- две любых первообразных для  на отрезке
на отрезке 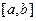 .Тогда
.Тогда
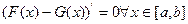 .Как следует из теоремы Лагранжа, это означает, что
.Как следует из теоремы Лагранжа, это означает, что 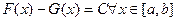 , где
, где 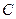 - некоторая фиксированная для всего отрезка константа.
- некоторая фиксированная для всего отрезка константа.
Мы только что доказали следующую теорему.
Теорема 1.1 Для того, чтобы две функции были первообразными для одной функции  на отрезке
на отрезке 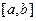 , необходимо и достаточно, чтобы они различались на константу.
, необходимо и достаточно, чтобы они различались на константу.
Определение 1.2. Совокупность всех первообразных функции  на отрезке
на отрезке 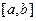 называется неопределённым интегралом функции
называется неопределённым интегралом функции  на отрезке
на отрезке 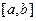 и обозначается
и обозначается 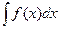 .
.
Если 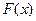 - какая-нибудь первообразная для
- какая-нибудь первообразная для 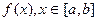 , то
, то 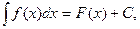 где
где 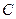 - произвольная константа.
- произвольная константа.
2.Свойства неопределённых интегралов.
Все свойства неопределённых интегралов вытекают из определения. Для их проверки (или доказательства) достаточно продифференцировать правую и левую части соответствующего равенства; если результаты совпадут, равенство верное.
2.1. 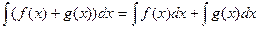 , если интегралы справа существуют;
, если интегралы справа существуют;
2.2. 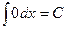 , где
, где 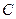 - произвольная постоянная; если
- произвольная постоянная; если 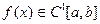 , то
, то
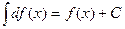 и
и 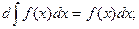
2.3.(Замена переменной) Если 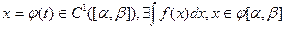 , то
, то
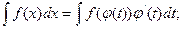
2.4. (Правило интегрирования по частям) 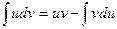 , если
, если 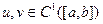 ;
;
2.5. Стандартная таблица простейших неопределённых интегралов:
1. 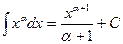 ,если
,если 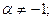
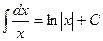 ;
;
2. 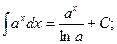
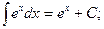
3. 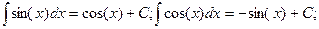
4. 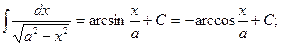
5. 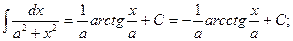
6. 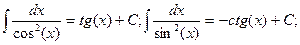
7. 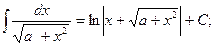
8. 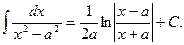
3. Можно заметить, что в стандартную таблицу не попали некоторые интегралы от простейших элементарных функций. Это произошло по двум причинам.
Во-первых, интегралы от логарифма, тангенса, котангенса, арксинуса, арккосинуса, арктангенса и арккотангенса легко вычисляются через приведённые. Во-вторых, в простейших случаях интеграл 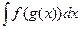 , где
, где 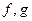 - простейшие элементарные функции
- простейшие элементарные функции
не выражается в конечном виде через простейшие элементарные функции(например,
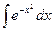 ).
).
Когда приходится вычислять (говорят: брать) интеграл от функции, которую Вы видите в первый раз, не факт, что Вам удастся подобрать такую конечную комбинацию элементарных функций, производной которой является подинтегральная функция.
Обычно, если сразу не видно, как свести предложенный интеграл к табличному, нужно попытаться упростить его, либо разбив на сумму более простых, либо испробовав какую-либо замену переменных. Часто встречающимися в задачниках заменами являются такие:
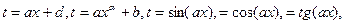 и так далее. Нужно помнить, что вместе с
и так далее. Нужно помнить, что вместе с  следует через новую переменную заменять и
следует через новую переменную заменять и 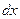 .Известно несколько типов интегралов,
.Известно несколько типов интегралов,
которые всегда выражаются в конечном виде через элементарные функции. Некоторые из них приведены ниже.
3.1. Рациональные дроби от одной переменной.
Так называются дроби вида
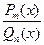 , где числитель – многочлен степени
, где числитель – многочлен степени 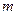 от
от  , знаменатель – многочлен степени
, знаменатель – многочлен степени 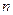 от
от  . Нас будет интересовать случай
. Нас будет интересовать случай 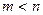 . Если это неравенство не выполняется, можно разделить числитель на знаменатель с остатком. Для остатка это неравенство будет выполняться.
. Если это неравенство не выполняется, можно разделить числитель на знаменатель с остатком. Для остатка это неравенство будет выполняться.
По одной из основных теорем алгебры, всякий многочлен 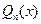 от одной переменной
от одной переменной  с действительными коэффициентами может быть однозначно разложен в произведение
с действительными коэффициентами может быть однозначно разложен в произведение
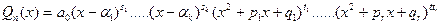 , где все коэффициенты - действительные числа,
, где все коэффициенты - действительные числа, 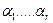 - все действительные корни этого многочлена, каждый со своей кратностью
- все действительные корни этого многочлена, каждый со своей кратностью 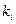 , а все квадратные трёхчлены не имеют действительных корней.
, а все квадратные трёхчлены не имеют действительных корней.
Для доказательства возможности выражения неопределённого интеграла от рациональной дроби в конечном виде через элементарные функции имеют значение следующие три факта. (1)Всякую правильную(с 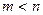 ) рациональную дробь можно разложить на простейшие; (2) Каждой скобке вида
) рациональную дробь можно разложить на простейшие; (2) Каждой скобке вида 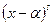 при этом разложении соответствует набор дробей
при этом разложении соответствует набор дробей
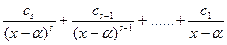 , а каждой скобке вида
, а каждой скобке вида 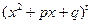 - набор дробей
- набор дробей 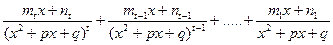 ; (3)Интеграл от дроби
; (3)Интеграл от дроби 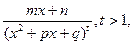 сводится к сумме рациональной дроби с интегралом от
сводится к сумме рациональной дроби с интегралом от 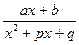 .
.
(Подробности можно посмотреть в «толстом» Фихтенгольце).Таким образом , интеграл от всякой рациональной дроби может быть выражен в виде суммы рациональной функции, логарифмов и арктангенсов в конечном числе.
3.2. Всякая рациональная функция от тригонометрических функций может быть приведена к обычной рациональной заменой 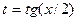 ; при замене в интеграле
; при замене в интеграле 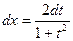 ,
, 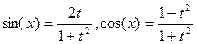 .
.
3.3.Рациональную функцию от 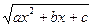 можно свести к обычной рациональной одной из замен Эйлера.
можно свести к обычной рациональной одной из замен Эйлера.
(1).Если 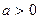 , можно сделать замену
, можно сделать замену 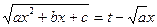 ; тогда
; тогда 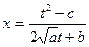 , и
, и 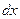 выражается через
выражается через 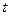 рационально.
рационально.
(2). Если 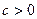 , положим
, положим 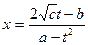 .
.
(3). Если подкоренное выражение имеет различные действительные корни 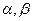 , положим
, положим
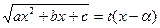 .
.
4. Вопросами о том, что делать, если интеграл не выражается в конечном виде через элементарные функции, мы заниматься не будем.
Определённый интеграл
1. Мы будем рассматривать функции, определённые на отрезке 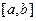 . Разбиением отрезка называется выбор точек
. Разбиением отрезка называется выбор точек 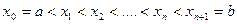 .(Неравенства могут быть в другую сторону, но все сразу). Мелкостью разбиения называется
.(Неравенства могут быть в другую сторону, но все сразу). Мелкостью разбиения называется 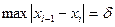 . Интегральной суммой для данного разбиения называется сумма вида
. Интегральной суммой для данного разбиения называется сумма вида
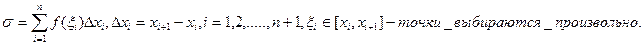
Определение 2.1. Определённым интегралом 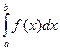 называется, если он существует,
называется, если он существует, 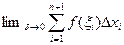 .Если определённый интеграл существует, функция называется интегрируемой по Риману на отрезке
.Если определённый интеграл существует, функция называется интегрируемой по Риману на отрезке 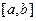 .
.
Отметим, что в определении не говорится ничего о выборе точек 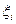 ; их можно выбирать любым способам, лишь бы
; их можно выбирать любым способам, лишь бы 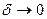 . То есть, никакие конкретные суммы при взятии предела не рассматриваются, ибо при любом фиксированном
. То есть, никакие конкретные суммы при взятии предела не рассматриваются, ибо при любом фиксированном 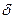 таких сумм бесконечно много. Тем не менее, рассмотрение интегральных сумм иногда полезно.
таких сумм бесконечно много. Тем не менее, рассмотрение интегральных сумм иногда полезно.
Следствие 1.1. Функция 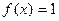 интегрируема, и
интегрируема, и 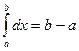 .
.
Действительно, для любого разбиения и любого выбора точек 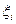 интегральная сумма равна
интегральная сумма равна 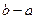 .
.
Теорема 2.1. Если функция интегрируема на отрезке 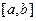 то она на нём ограничена.
то она на нём ограничена.
Доказательство. Предположим, что  не ограничена в точке
не ограничена в точке 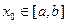 .При любом
.При любом 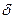 , можно выбирать точки
, можно выбирать точки 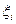 так, чтобы: 1)произведение
так, чтобы: 1)произведение 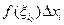 для отрезка
для отрезка 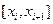 , на котором лежит точка
, на котором лежит точка 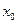 , было сколь угодно большим по модулю; 2) чтобы остающаяся часть интегральной суммы была по модулю меньше половины модуля указанного произведения. Если функция интегрируема, у таких интегральных сумм должен быть конечный предел, что противоречит принципу их построения. Теорема доказана.
, было сколь угодно большим по модулю; 2) чтобы остающаяся часть интегральной суммы была по модулю меньше половины модуля указанного произведения. Если функция интегрируема, у таких интегральных сумм должен быть конечный предел, что противоречит принципу их построения. Теорема доказана.
В дальнейшем мы будем рассматривать только ограниченные на отрезке функции.
Теорема 2.2.Если функция на отрезке 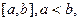 интегрируема и не отрицательна, то интеграл от неё не меньше нуля.
интегрируема и не отрицательна, то интеграл от неё не меньше нуля.
