Классы интегрируемых функций 1 страница
ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Краткое содержание лекций по математическому анализу для студентов 1-го курса Экономического факультета МГУ (теория).
Введение
Это, за указанными в тексте исключениями(их всего одно или два), – реально прочитанная теория.
Автор всю жизнь придерживался убеждения, что если читать курс математической дисциплины даже не на естественном факультете, он всё равно должен быть построен так, чтобы те студенты, которые хотят понять, откуда берутся те или другие утверждения, смогли бы это сделать. Все утверждения , касающиеся последовательностей, доказываются. В дальнейшем доказываются только те утверждения, которые нельзя получить с помощью эквивалентности Гейне-Коши, и все принципиальные теоремы. Необходимые примеры приводятся в минимальных размерах. На лекциях их приводилось гораздо больше, равно как и доказательства сопровождались рисунками и прочими способствующими пониманию подробностями. Предлагаемый текст предназначен только для того, чтобы вся теория была под рукой в сжатом изложении.
Это – не учебник матанализа для среднего студента. Это – справочный материал. При написании автор пользовался(как и при чтении лекций) различными стандартными учебниками, в основном – «Курсом дифференциального и интегрального исчислений» Г.М.Фихтенгольца,тт.1-3.
Первый семестр
Предполагается, что читающий знаком с курсом арифметики, алгебры, тригонометрии и началами геометрии в объёме средней школы. Желательно, но не обязательно, чтобы он знал что-нибудь о понятии производной.
В частности, предполагается, что читатель знает, как выглядят графики функций y=ax+b, y=ax2+bx+c, y=x 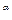 , y=ax, y=logax, y=sin(x), y=cos(x), y=tg(x), y=ctg(x), y=arcsin(x), y=arccos(x), y=arctg(x), y=arcctg(x).
, y=ax, y=logax, y=sin(x), y=cos(x), y=tg(x), y=ctg(x), y=arcsin(x), y=arccos(x), y=arctg(x), y=arcctg(x).
Для дальнейшего будут существенны следующие свойства функции y = |x|:
|xy|=|x||y|;|x+y| 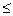 |x|+|y|;|x-y|
|x|+|y|;|x-y| 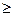 ||x|-|y||.
||x|-|y||.
Предполагается также, что известны словосочетания: числовая прямая, вещественное число, числовая ось, действительное число, целое число, рациональное число.
Множество натуральных чисел N есть множество {1,2,3…..}.Множество целых чисел Z есть множество {0,-1,+1,-2,+2,….}.Множество рациональных чисел Q есть множество {p/q | p 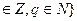 . Множество действительных (или вещественных) чисел будет обозначаться R.
. Множество действительных (или вещественных) чисел будет обозначаться R.
Для стандартных подмножеств множества R будут употребляться обозначения:
[a,b] = 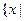
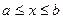 }(отрезок);
}(отрезок);
(a,b]( 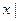
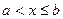 } (левый полуинтервал);
} (левый полуинтервал);
(a,b)= 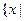 a<x<b}(интервал);
a<x<b}(интервал);
[a,b) = {x| a 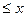 <b}(правый полуинтервал).
<b}(правый полуинтервал).
Множество типа {x| a 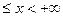 } называется замкнутым лучом, равно как и множество вида {x| -
} называется замкнутым лучом, равно как и множество вида {x| - 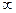 < x
< x 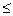 a}; если убрать знаки равенства, получится открытый луч.
a}; если убрать знаки равенства, получится открытый луч.
Множество точек числовой оси называется ограниченным, если найдётся отрезок, на котором всё оно расположено.
Пусть 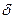 >0.
>0.
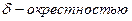 точки
точки 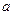 называется интервал (a -
называется интервал (a - 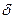 ,a+
,a+ 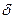 ).
). 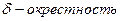 точки a называется проколотой, если рассматриваются все её точки, кроме a. Проколотая
точки a называется проколотой, если рассматриваются все её точки, кроме a. Проколотая 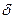 окрестность точки a,таким образом, это объединение интервалов (a -
окрестность точки a,таким образом, это объединение интервалов (a - 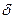 ,a )
,a ) 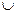 (a , a +
(a , a + 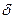 ).
).
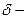 окрестностью «точки»
окрестностью «точки» 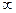 называется множество точек x числовой оси, для которых
называется множество точек x числовой оси, для которых 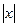 >
> 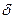 .
.
1.Кое-что о множествах.
Вопрос о том, что такое множество, здесь обсуждаться не будет. Обычно, когда говорят о множествах, говорящие имеют в виду некое собрание известных им элементов.
Пусть A и B  - множества. Их пересечением называется множество C=A
- множества. Их пересечением называется множество C=A 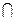 B,каждая точка которого принадлежит и A и B.
B,каждая точка которого принадлежит и A и B.
Объединением множеств A и B называется множество A 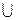 B ,состоящее из тех, и только тех точек, которые принадлежат либо A,либо B.
B ,состоящее из тех, и только тех точек, которые принадлежат либо A,либо B.
Разностью множеств 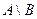 называется множество, состоящее из тех элементов
называется множество, состоящее из тех элементов 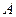 , которые не принадлежат
, которые не принадлежат 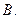
Симметрической разностью 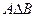 называется множество
называется множество 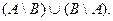
1.1.Легко понять, что пересечение двух окрестностей одной точки будет окрестностью этой точки(меньшей по размеру), и объединение двух окрестностей одной точки тоже будет окрестностью этой точки –(большей).Аналогичные утверждения верны для любого конечного числа окрестностей одной и той же точки.
1.2.Множество А точек числовой оси называется ограниченным сверху, если найдётся число М, такое, что для всех x 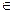 A выполняется неравенство x
A выполняется неравенство x 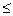 М. Число М называется в этом случае верхней гранью множества А. Число М
М. Число М называется в этом случае верхней гранью множества А. Число М 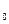 называется точной верхней гранью множества А, если (1) оно является верхней гранью множества А, и (2) если никакое число N <M
называется точной верхней гранью множества А, если (1) оно является верхней гранью множества А, и (2) если никакое число N <M 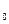 верхней гранью множества А не является (иными словами, всё множество А лежит на луче(-
верхней гранью множества А не является (иными словами, всё множество А лежит на луче(- 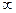 ,М
,М 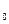 ], и в любом полуинтервале (M
], и в любом полуинтервале (M 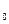 -
- 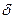 ,M
,M 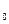 ] есть хотя бы одна точка x
] есть хотя бы одна точка x 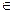 A.Точная верхняя грань множества А обозначается обычно, supA. Точная верхняя грань множества {-x,x
A.Точная верхняя грань множества А обозначается обычно, supA. Точная верхняя грань множества {-x,x 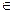 A}=-A , взятая с минусом, называется точной нижней гранью множества A и обозначается обычно infA. Множество А называется неограниченным сверху, если у него нет точной верхней грани, и неограниченным снизу, если у него нет точной нижней грани. Мы будем считать, что для числовых множеств выполнена следующая аксиома.
A}=-A , взятая с минусом, называется точной нижней гранью множества A и обозначается обычно infA. Множество А называется неограниченным сверху, если у него нет точной верхней грани, и неограниченным снизу, если у него нет точной нижней грани. Мы будем считать, что для числовых множеств выполнена следующая аксиома.
Аксиома. Всякое ограниченное сверху множество А имеет точную верхнюю грань.
У этой аксиомы есть много эквивалентных ей утверждений. Они будут в дальнейшем отмечаться по мере появления. Фактически она означает непрерывность числовой прямой.
2.Теория последовательностей
Определение 2.1. Последовательностью называется бесконечное множество вещественных чисел, занумерованных натуральным рядом, то есть последовательность - это множество{a(n)},каждому элементу которого присвоен некоторый номер; а(n) – это элемент с номером n.
Определение 2.2.Последовательность b(m) называется подпоследовательностью последовательности a(n),если любой её элемент является элементом последовательности a(n),b(m) = a(n) для некоторого n, и для любых m 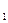 < m
< m 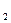 выполняется неравенство n
выполняется неравенство n 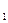 <n
<n 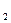 , то есть в подпоследовательности элементы идут в том же порядке, что и в последовательности. Иными словами, подпоследовательность получается из последовательности вычёркиванием некоторого, может быть бесконечного, числа элементов, но так, что при этом остаётся бесконечное число элементов, и порядок оставшихся элементов не меняется.
, то есть в подпоследовательности элементы идут в том же порядке, что и в последовательности. Иными словами, подпоследовательность получается из последовательности вычёркиванием некоторого, может быть бесконечного, числа элементов, но так, что при этом остаётся бесконечное число элементов, и порядок оставшихся элементов не меняется.
Последовательности можно складывать, вычитать, перемножать , делить, если последовательность в знаменателе не имеет нулевых элементов, и брать от них разнообразные функции( по формуле f{a(n)} = {f(a(n))}).По определению, если {a(n)}и {b(n)} – две последовательности, то (a+b)(n) = a(n) + b(n);(a – b)(n)=a(n) – b(n); (ab)(n) = a(n)b(n); (a /b)(n) = a(n)/b(n); 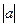 (n) =
(n) = 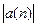 .Иными словами, все операции над последовательностями, определённые выше, выполняются поэлементно.
.Иными словами, все операции над последовательностями, определённые выше, выполняются поэлементно.
2.1.Последовательности ,имеющие предел(сходящиеся последовательности).
Определение 2.3.Говорят, что последовательность a(n) имеет предел l,если для всякого  >0 найдётся такой номер n(
>0 найдётся такой номер n(  ), что для всякого номера m
), что для всякого номера m 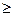 n(
n(  ) ,будет выполняться неравенство
) ,будет выполняться неравенство 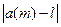 <
<  .Говорят, что последовательность a(n) сходится к l.Иначе можно сказать, последовательность а(n) сходится к l,если для любого
.Говорят, что последовательность a(n) сходится к l.Иначе можно сказать, последовательность а(n) сходится к l,если для любого  > 0 найдётся такая окрестность точки +
> 0 найдётся такая окрестность точки + 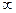 (а именно, [n(
(а именно, [n(  ),+
),+ 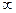 ) = U
) = U 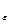 (+
(+ 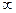 )), что для всех m
)), что для всех m 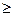 n(
n(  ) элементы a(m) попадают в
) элементы a(m) попадают в  -окрестность точки l(которую можно обозначить U
-окрестность точки l(которую можно обозначить U 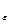 (l)). Пишут:
(l)). Пишут: 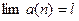 .
.
Примечание. Эта «окрестностная» точка зрения очень важна. Практически все утверждения, которые можно получить с её помощью, сохраняются в том случае, если при определении понятия окрестности оказывается, что две непустых окрестности одной точки пересекаются по непустой окрестности той же точки, и если для некоторой операции ,определяемой для любой пары элементов рассматриваемого множества как 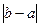 ,сохраняются те же свойства,
,сохраняются те же свойства,  что для обычной абсолютной величины. Более того, доказательства утверждений, приводимые в дальнейшем, достаточно часто выглядят следующим образом: строится несколько окрестностей точки, в каждой из которых выполняется некоторое утверждение; тогда в пересечении этих окрестностей выполняются все утверждения одновременно; обычно выполнение всех этих утверждений обеспечивает доказательство исходного утверждения.
что для обычной абсолютной величины. Более того, доказательства утверждений, приводимые в дальнейшем, достаточно часто выглядят следующим образом: строится несколько окрестностей точки, в каждой из которых выполняется некоторое утверждение; тогда в пересечении этих окрестностей выполняются все утверждения одновременно; обычно выполнение всех этих утверждений обеспечивает доказательство исходного утверждения.
Лемма 2.1.1(об устойчивости знака).Если lim a(n) = l 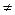 0, то найдётся окрестность точки +
0, то найдётся окрестность точки + 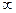 , в которой a(n) имеет тот же знак, что и l.Иными словами, найдётся такой номер т
, в которой a(n) имеет тот же знак, что и l.Иными словами, найдётся такой номер т 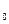 , что для всех т
, что для всех т 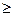 m
m 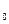 a(m) будет иметь тот же знак, что и l.
a(m) будет иметь тот же знак, что и l.
Доказательство. Мы докажем больше, а именно, что если l 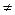 0, то найдётся номер m
0, то найдётся номер m 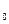 , начиная с которого для всех m будет
, начиная с которого для всех m будет 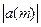
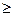 |l/2|. Действительно, поскольку lim a(m) = l, для всякого
|l/2|. Действительно, поскольку lim a(m) = l, для всякого  >0 найдётся такой номер m
>0 найдётся такой номер m 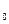 , начиная с которого будет
, начиная с которого будет 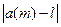 <
<  , или, по определению модуля, -
, или, по определению модуля, -  <a(m) – l <
<a(m) – l <  , или, что то же самое, l -
, или, что то же самое, l -  <a(m)< l +
<a(m)< l +  . Выбирая теперь
. Выбирая теперь  =| l/2|, получим l-
=| l/2|, получим l- 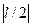 < a(m) <l +
< a(m) <l + 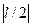 . Очевидно, левая и правая части этого двойного неравенства имеют один знак. Лемма доказана.
. Очевидно, левая и правая части этого двойного неравенства имеют один знак. Лемма доказана.
Примечание. Вместо l/2 можно взять 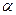 l, где
l, где 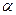
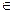 [0,1).
[0,1).
Лемма 2.1.2.Последовательность, имеющая предел, ограничена.
Доказательство. Пусть lim a(n) = l. Это означает, что для  >0 найдётся номер т
>0 найдётся номер т 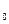 ,такой, что для всех m
,такой, что для всех m 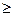 m
m 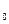 будет выполняться неравенство l -
будет выполняться неравенство l -  <a(m)<l +
<a(m)<l +  .То есть все элементы последовательности будут лежать на интервале (l -
.То есть все элементы последовательности будут лежать на интервале (l - 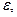 l +
l +  ), кроме конечного числа m
), кроме конечного числа m 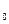 - 1 ,которые там , может быть , не лежат. Расширив полученный интервал до отрезка, включающего все эти элементы, получим, что лемма доказана.
- 1 ,которые там , может быть , не лежат. Расширив полученный интервал до отрезка, включающего все эти элементы, получим, что лемма доказана.
Определение 2.4. Если lim a(n) = 0, говорят, что последовательность a(n) бесконечномалая.
Лемма 2.1.3.Произведение ограниченной последовательности на бесконечномалую является бесконечномалой последовательностью. Сумма бесконечномалых последовательностей в конечном числе является бесконечномалой последовательностью.Модуль бесконечномалой последовательности – бесконечномалая.
Доказательство.(a).Пусть a(n) – бесконечномалая, а b(n) – ограниченная.Тогда существует такой номер n 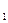 ,что для всех n
,что для всех n 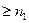 будет выполнятьсянеравенство
будет выполнятьсянеравенство 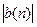
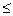 M для некоторого M(ограниченность), и для произвольного
M для некоторого M(ограниченность), и для произвольного  при
при 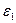 =
= 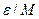 найдётся такой номер n
найдётся такой номер n 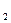 ,что для всех n
,что для всех n 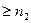 будет выполняться неравенство
будет выполняться неравенство 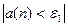 .Тогда для n
.Тогда для n 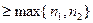 имеем
имеем 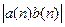 <
<  . Значит,a(n)b(n) – бесконечномалая.
. Значит,a(n)b(n) – бесконечномалая.
(б).Пусть a(n),b(n) –бесконечномалые. Пусть 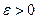 - произвольно. Для произвольных
- произвольно. Для произвольных 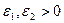 ,в частности, для
,в частности, для 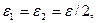 найдутся такие номера n
найдутся такие номера n 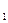 ,n
,n 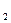 ,соответственно, что будут иметь место неравенства
,соответственно, что будут иметь место неравенства 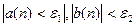 при n
при n 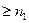 ,n
,n 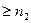 ,соответственно. Значит,
,соответственно. Значит, 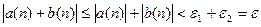 при n
при n 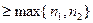 , и a(n) + b(n) – бесконечномалая.
, и a(n) + b(n) – бесконечномалая.
Для модуля доказательство очевидно из определения бесконечномалой.Лемма доказана.
Замечание. Вместо двух бесконечномалых можно было взять их любое конечное количество. Доказательство очевидно.
Лемма 2.1.4.Если lima(n) = l, то 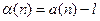 - бесконечномалая, и наоборот,если
- бесконечномалая, и наоборот,если 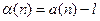 - бесконечномалая, то lima(n) = l.
- бесконечномалая, то lima(n) = l.
Доказательство очевидно.
Лемма 2.1.5. Пусть lim a(n) = l 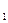 ,lim b(m) = l
,lim b(m) = l 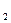 .Тогда
.Тогда
lim(a(n) + b(n)) = l 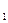 +l
+l 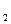 ; lim(a(n) – b(n)) = l
; lim(a(n) – b(n)) = l 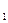 - l
- l 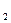 ; lim(a(n)b(n)) = l
; lim(a(n)b(n)) = l 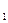 l
l 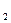 ;lim
;lim 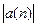 =
= 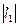 и lim
и lim 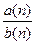 =
= 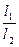 , если b(n) не обращается в 0 и
, если b(n) не обращается в 0 и 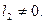
Доказательство. Во всех случаях достаточно доказать, что разность между правой и левой частями есть бесконечномалая. Имеем:
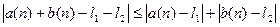 - по Лемме 2.1.2,сумма бесконечномалых есть
- по Лемме 2.1.2,сумма бесконечномалых есть
бесконечномалая. Для разности доказательство аналогичное.
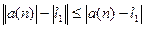 - значит, предел модуля равен модулю предела.
- значит, предел модуля равен модулю предела.
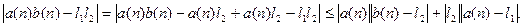 Первое слагаемое справа – это произведение ограниченной на бесконечномалую, второе - то же. Значит, предел произведения равен произведению пределов
Первое слагаемое справа – это произведение ограниченной на бесконечномалую, второе - то же. Значит, предел произведения равен произведению пределов


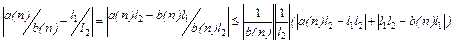 .
.
Согласно Лемме 2.1.1.,найдётся n 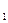 ,начиная с которого (то есть, для n
,начиная с которого (то есть, для n 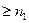 ) ,будет
) ,будет 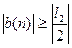 , то есть, выражение перед круглой скобкой будет ограничено. Оба выражения в круглых скобках будут бесконечномалыми. Значит, всё выражение будет бесконечномалым, и, значит, предел частного будет равен частному пределов.
, то есть, выражение перед круглой скобкой будет ограничено. Оба выражения в круглых скобках будут бесконечномалыми. Значит, всё выражение будет бесконечномалым, и, значит, предел частного будет равен частному пределов.
Лемма доказана
Лемма 2.1.6.Пусть 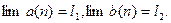 Тогда, если
Тогда, если 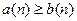 начиная с некоторого
начиная с некоторого 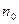 , то
, то 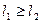 .
.
Доказательство. Предположим, что 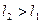 . Тогда
. Тогда 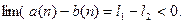 Согласно лемме об устойчивости знака, начиная с некоторого
Согласно лемме об устойчивости знака, начиная с некоторого 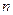 будет выполняться неравенство
будет выполняться неравенство 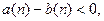 что противоречит условию.
что противоречит условию.
Лемма доказана.
Замечание. Нельзя утверждать, что 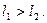 Пусть, например,
Пусть, например, 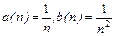 .Очевидно, начиная с
.Очевидно, начиная с 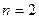 ,
, 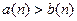 , но
, но 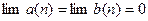 .
.
Лемма 2.1.7(о двух милиционерах). Пусть , начиная с некоторого 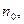
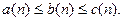 Тогда, если
Тогда, если 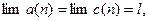 то существует и
то существует и 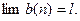
Доказательство. Пусть 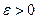 взято произвольно. Согласно условию, начиная с некоторого
взято произвольно. Согласно условию, начиная с некоторого 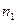 , будет
, будет 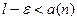 , а начиная с некоторого
, а начиная с некоторого 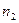 будет
будет 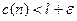 .Тогда при
.Тогда при 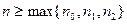 имеем:
имеем: 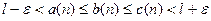 ,или
,или 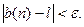
Лемма доказана.
Лемма 2.1.8. Возрастающая ограниченная сверху последовательность имеет предел.
Доказательство. Поскольку последовательность  ограничена, у неё есть точная верхняя грань (согласно аксиоме!)
ограничена, у неё есть точная верхняя грань (согласно аксиоме!) 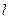 . Пусть
. Пусть 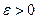 взято произвольно. Рассмотрим полуинтервал (
взято произвольно. Рассмотрим полуинтервал ( 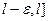 . Найдётся элемент последовательности
. Найдётся элемент последовательности 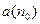 , принадлежащий этому полуинтервалу (в противном случае
, принадлежащий этому полуинтервалу (в противном случае 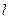 не есть точная верхняя грань
не есть точная верхняя грань 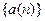 ). Поскольку последовательность
). Поскольку последовательность  - возрастающая, для всех
- возрастающая, для всех 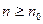
 будет принадлежать тому же полуинтервалу, то есть будет выполняться неравенство
будет принадлежать тому же полуинтервалу, то есть будет выполняться неравенство 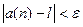 (Знак
(Знак 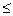 в этих условиях невозможен. Почему? ). Согласно определению предела последовательности,
в этих условиях невозможен. Почему? ). Согласно определению предела последовательности, 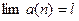 . Лемма доказана.
. Лемма доказана.
