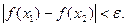Классы интегрируемых функций 2 страница

Следствие. Всякая неубывающая последовательность, ограниченная сверху, имеет предел. Всякая невозрастающая последовательность, ограниченная снизу, имеет предел.

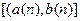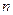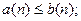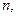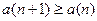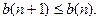Лемма 2.1.9(о стягивающихся отрезках). Пусть дана последовательность отрезков , удовлетворяющая следующим трём условиям:(1) для всякого , (2) для всякого одновременно выполняются неравенства и (3) 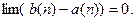Тогда существует ровно одна точка, принадлежащая всем этим отрезкам.

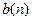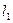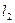Доказательство. Рассмотрим две последовательности: последовательность левых концов, , и последовательность правых концов, .Первая из них неубывающая и ограниченная сверху, вторая – невозрастающая и ограниченная снизу. По предыдущему следствию, обе они имеют пределы и , соответственно. Поскольку для любого 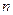и для любого 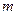всегда будет 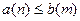, то будут выполняться и неравенства 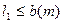и 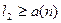.Следовательно, 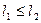.В частности, при 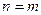получим 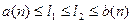, откуда 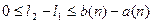.Предел выражения справа равен 0 по условию. Значит, 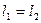. Лемма доказана.

Примечание 1. Леммы 2.1.8 и 2.1.9 эквивалентны основной Аксиоме.

Примечание 2. Если в условии Леммы заменить отрезки на интервалы или полуинтервалы, её утверждение, вообще говоря, не будет иметь места. Если же отказаться от условия (3), то общих точек будет много, целый отрезок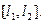

2.2.Последовательности, не имеющие предела.

Определение 2.5.Точка 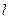называется предельной точкой последовательности (множества 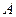), если в любой проколотой окрестности этой точки есть хотя бы один элемент последовательности (множества ).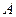

Определение 2.6. Точка 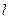называется изолированной точкой множества 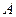, если она принадлежит множеству 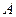и если существует окрестность точки 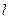, в которой нет других точек множества .

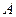Примеры: (1) У последовательности 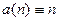все точки – изолированные.

(2) У последовательности 1;1;2;1:3;1;4;…… точка 1 является предельной.

Лемма 2.2.1. Всякая ограниченная последовательность имеет хотя бы одну предельную точку, и существует подпоследовательность, сходящаяся к этой точке.

Доказательство. Оба утверждения будут доказываться вместе.

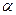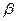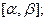Пусть - рассматриваемая последовательность. Она по условию ограничена, значит у неё существуют конечные точные грани, нижняя - , и верхняя - . Все элементы лежат на отрезке поделим его пополам. Хотя бы на одной из половин будет лежать бесконечное число элементов последовательности (в противном случае их число было бы конечным на всём 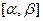). Из элементов, лежащих на этой половине, произвольно выберем какой-нибудь, например, 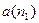. Концы этой половины обозначим (слева направо!) 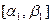.Поделим выбранную половину отрезка опять пополам. На одной из двух образовавшихся половин (четвертинок первоначального 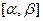) опять окажется бесконечное число элементов . Выберем среди них элемент 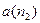так чтобы было 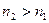, обозначим концы выбранной половинки 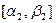и продолжим деление пополам. Те половинки, которые мы выбираем, образуют систему стягивающихся отрезков 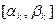, по длине стремящихся к 0. У них, по Лемме о стягивающихся отрезках, есть общая точка 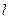. 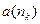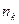Элементы , которые мы выбирали, образуют подпоследовательность последовательности ,так как номера возрастают. Покажем, что 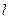- предел этой подпоследовательности. Если 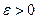выбрано произвольно, мы всегда можем указать номер 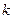, для которого длина очередной половинки будет меньше, чем 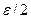.Так как 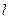и 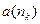лежат на этой половинке, и все последующие 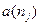для 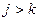будут лежать там же, то неравенство 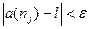будет выполняться для всех 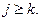Значит, 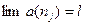. В любой проколотой окрестности точки 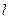будет содержаться хотя бы одна точка последовательности (в силу правила выбора половинок отрезков). Значит, 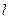будет предельной точкой последовательности 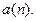Лемма доказана.

Если последовательность не ограничена, она может не иметь предельных точек: (1) 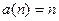, или (2) иметь: .

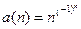В случае (2) предельных точек может быть сколько угодно (например, вся числовая прямая, то есть все действительные числа могут быть предельными точками одной последовательности). Для ограниченных последовательностей предельные точки могут иметься в любом конечном количестве, или их число может быть бесконечным, в частности, они могут заполнять отрезок, полуинтервал или интервал.

Определение 2.7.Точная нижняя грань множества предельных точек последовательности (конечная или бесконечная) называется нижним пределом последовательности и обозначается 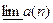; точная верхняя грань множества предельных точек последовательности (конечная или бесконечная) называется верхним пределом последовательности и обозначается .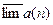

Примеры:1.У последовательности 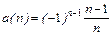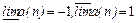;2.У последовательности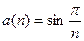 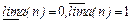;3.У последовательности .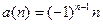

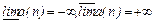Лемма 2.2.2.(Критерий Коши). Для того чтобы последовательность сходилась, необходимо и достаточно, чтобы для неё выполнялось следующее условие(условие Коши): для всякого 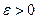существует 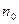, такое, что для любых 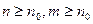имеет место неравенство .

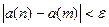Доказательство.(1) Необходимость: если последовательность сходится, условие выполняется.

Если 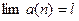, то по 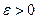найдётся такой номер 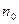, что для всех 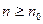будет выполняться неравенство 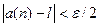.Для любых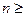 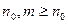будем иметь

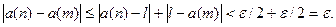Условие выполнено.

(2) Достаточность. Если условие выполнено, последовательность сходится. Пусть условие выполнено. Возьмём какое-нибудь 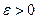, найдём по нему 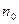.Тогда для всех 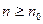будет выполняться неравенство 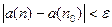или 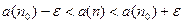. Отсюда следует, что ограничена (так как вне интервала 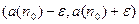находится конечное число членов последовательности). Поскольку ограничена, у неё есть предельные точки. Если предельная точка всего одна, то это и есть 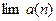.(Почему?) Предположим, что есть две разных предельных точки, 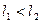. Возьмём 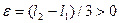. Существуют подпоследовательности последовательности 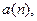сходящиеся к этим предельным точкам. Пусть подпоследовательность 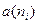сходится к 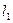, а подпоследовательность 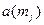- к 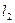.По выбранному , из условия Коши найдём 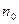, такое что для всех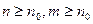 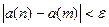; найдутся также 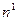и 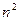, такие что для 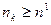и 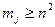будут выполняться неравенства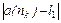 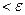и 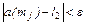, соответственно. Имеем

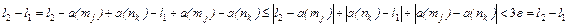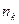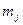
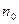если и будут не меньше . Полученное противоречие показывает, что предельная точка у нашей последовательности всего одна. Лемма доказана.

Примечание. Критерий Коши эквивалентен основной Аксиоме.

3.Предел функции

Пусть имеется функция f(x), определённая в проколотой окрестности U(x 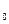) (или в одной из полуокрестностей).

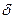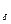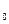Определение 3.1.Пределом функции f(x) в точке x называется число A,если для всякого >0 найдётся >0,такое, что для всех x из U (x 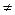),x x , .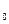

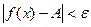Это определение называется определением предела функции по Коши.

Другие формулировки.1.Обозначение 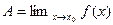.2.Говорят, что предел функции равен A при стремлении точки x к точке , если при стремлении к нулю

разности x-x 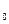стремится к нулю разность f(x) – A.3.A = lim 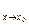f(x), если для всякого 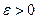найдётся такое 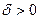, что для всех 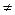x x 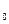,для которых выполняются неравенства 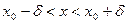,будут выполняться неравенства .

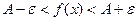4. .

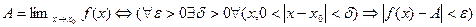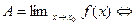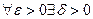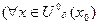
5. ( ) 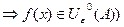.Символом U 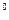обозначается проколотая окрестность.

Определение 3.2.Число A называется пределом функции ,определённой в некоторой про­ко­лотой окрестности точки ,если для любой последовательности точек 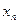,принадлежащей ука­занной окрестности и сходящейся к , последовательность значений функции 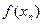сходится к A.

Это определение предела называется определением предела функции по Гейне.

Теорема 3.1.Определения предела функции по Коши и по Гейне эквивалентны.

Доказательство.1.Пусть 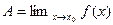по Коши. Тогда для любого 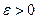найдётся 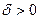, такое, что 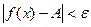для всех 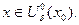Пусть теперь 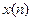- произвольная последовательность, сходящаяся к точке 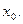Согласно определению предела последовательности, найдётся такое 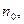что при 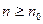всегда будет 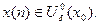Поэтому, начиная с 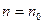,будет выполняться неравенство 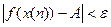, и мы получили: 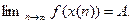Значит 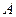- предел по Гейне.

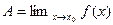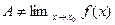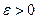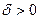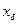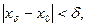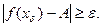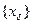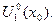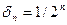2.Пусть теперь по Гейне. Предположим, что по Коши. Тогда найдётся , такое, что для любого 1> найдётся такой , что с одной стороны, а с другой стороны, Множество точек является ограниченным: оно всё принадлежит окрестности Пусть .Тогда 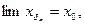но 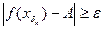и, значит, 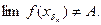Мы нашли последовательность, сходящуюся к и такую, что соответствующая последовательность значений функции не сходится к 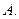Это противоречит предположению, что 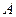- предел по Гейне. Теорема доказана.

Следствие 3.1. Леммы 2.1.1 – 2.1.8 справедливы для функций, имеющих предел в точке, при соответствующей переформулировке. А именно

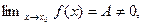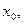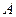3.1.1.Если то найдётся окрестность точки в которой значение отличается от менее, чем на 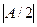; в частности, знак для всех из этой окрестности будет совпадать со знаком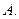

3.1.2.Если 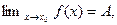то 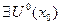,в которой ограничена.

3.1.3.Пусть в некоторой окрестности 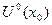функция - бесконечномалая при 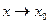, 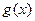- ограниченная. Тогда 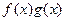- бесконечномалая. Сумма конечного числа бесконечномалых есть функция бесконечномалая. Модуль бесконечномалой функции – бесконечно малая.

3.1.4.Если 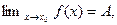то 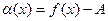- бесконечномалая функция при 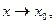и обратно.

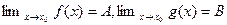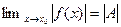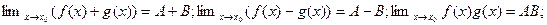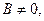3.1.5.Пусть . Тогда ; если то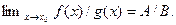

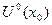
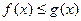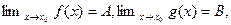3.1.6.Если в некоторой окрестности и то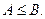

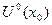
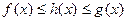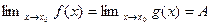3.1.7.Если в некоторой окрестности и , то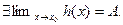

3.1.8.Пусть при 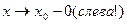монотонно возрастает и ограничена. Тогда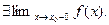

3.2.Критерий Коши для функций. Пусть определена в некоторой 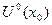.Для того, чтобы существовал 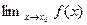, необходимо и достаточно, чтобы для любого 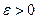нашлось 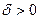такое, что для любых 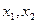из 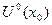,для которых 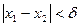, выполнялось неравенство