Дифференциальное исчисление функций одной переменной 2 страница

Найти .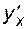

Решение.

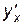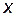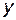Пример 4.4. Найти , если переменные и связаны соотношением

.

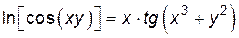Решение.

Явно выразить одну из переменных через другую невозможно, поэтому находим производные левой и правой частей данного равенства и приравниваем их:

.

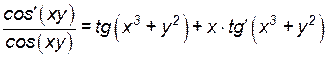Далее имеем:

;

.

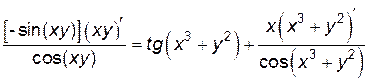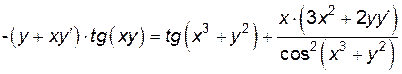Перенося слагаемые, содержащие 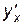, в одну часть равенства, вынося 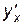за скобку, а остальные слагаемые – в другую и деля на коэффициент при 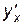, получаем:

.

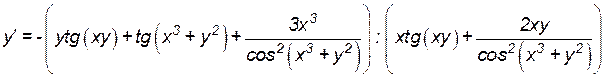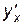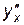Пример 4.5. Найти и для функции, заданной параметрически:

.

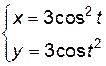Решение

; ;

;
;

;

.

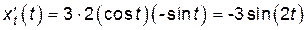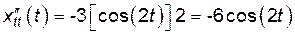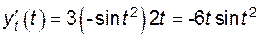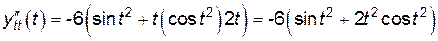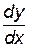
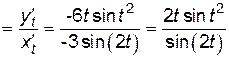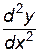
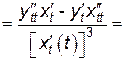
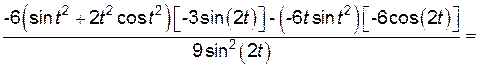
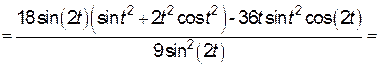
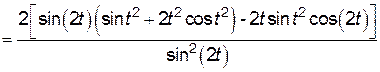4.4. Логарифмическое дифференцирование

Рассмотрим показательно-степенную функцию 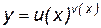, где 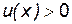, u(x), v(x) – дифференцируемые функции.

Прологарифмируем равенство 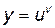, получим: 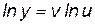(по свойствам логарифмов). Дифференцируем обе части полученного равенства как неявную функцию, помня, что y – функция от x:

,

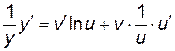откуда .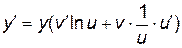

Подставляя сюда 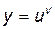, имеем:

.

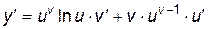Этот прием нахождения производной называется логарифмическим дифференцированием.

Пример 4.6. Найти .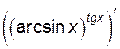

Решение.

Вначале прологарифмируем данное равенство

,

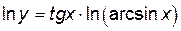и найдем производные от обеих частей полученного равенства, приравнивая их:

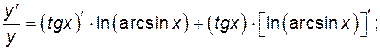
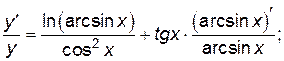
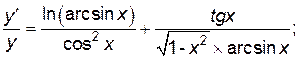
Учитывая, что 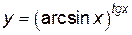, имеем:

.

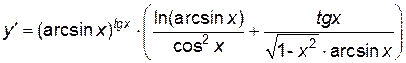Пример 4.7. 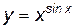, (x > 0). Найти производную функции y'.

Решение.

,

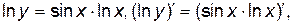
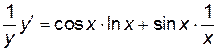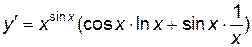или .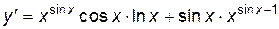

5. Производные высших порядков

5.1. Понятие производной высшего порядка

Пусть функция 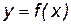определена и дифференцируема на некотором промежутке X, тогда ее производная 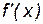также является функцией от x на этом промежутке. Если 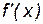имеет производную на промежутке X, то эта производная называется производной второго порядкафункции y = f(x) и обозначается: y'' или .

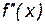Итак,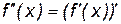

Производная от производной второго порядка называетсяпроизводной третьего порядкаи обозначается: y''' или .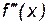

Вообще, производной n-го порядка называется производная от производной 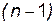-го порядка и обозначается: y⁽ⁿ⁾ или f ⁽ⁿ⁾(x). Итак,

f ⁽ⁿ⁾(x) = (f ^(n-1)(x))'.

Производные y'', y''', ... называются производными высших порядков.

Пример 5.1. 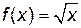. Найти 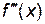и .

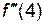Решение.

= = ,

= – ,

= = ,

= = = .

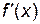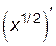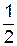
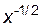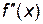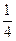
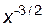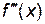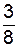
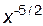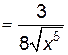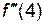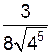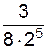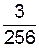Пример 5.2. Найти производную n-го порядка для функции .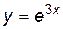

Решение.

,

,

.

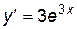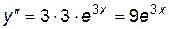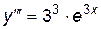По аналогии находим: .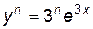

5.2. Производные высших порядков от функций,
заданных параметрически

Пусть функция y, зависящая от x, задана параметрически на интервале Т:

,

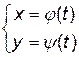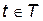
Найдем 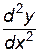. Известно, что 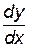= = 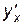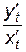(п. 4.3), поэтому

= = = = .

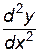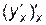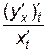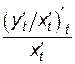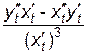Аналогично будет вычисляться 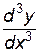и т. д.

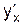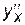Пример 5.3. Найти и для функции, заданной параметрически:

.

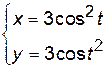Решение.

;

;

;

;

;

=

.

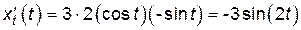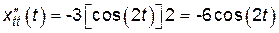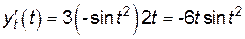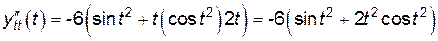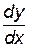
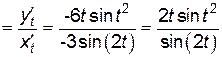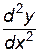
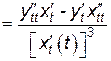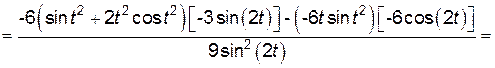
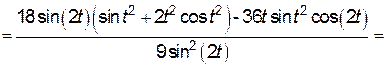
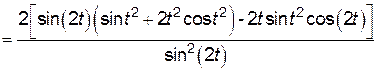Пример 5.4. Функция y от x задана параметрически уравнениями:

, .

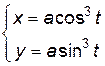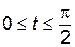Найти .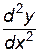

Решение.

= = = = ;

= = =- = .

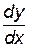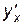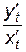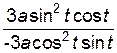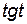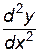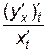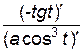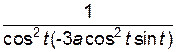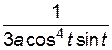5.3. Производные высших порядков от функций,
заданных неявно

Нахождение производных высших порядков от функций, заданных неявно, рассмотрим на примере.

Пример 5.5. Найти 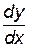, 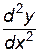для функции, заданной неявно уравнением: 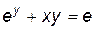. Вычислить y'(0), y''(0).

Решение.

Найдем сначала y', как описано в п.4.2.

,

,

,

= .

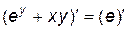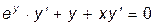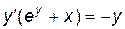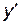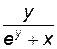Для нахождения y'' будем дифференцировать равенство 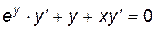, получим:

.

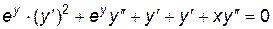Отсюда найдем y'' и подставим найденное выражение для y': ,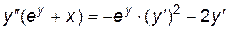

y''=– = = =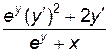

= .

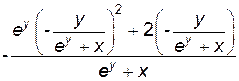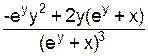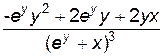Итак, y'=– ,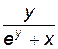

y''= .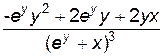

Подставим x=0 в исходное уравнение 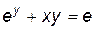, получим:

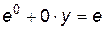, откуда y=1, значит,

y(0)=1; y'(0)=– 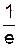; y''(0)= = .

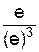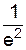6. Правило Лопиталя

Рассмотрим новый способ нахождения пределов отношения двух бесконечно малых или бесконечно больших функций, т.е. раскрытия неопределенностей типа 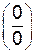и 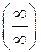, так называемое правило Лопиталя.

Теорема Лопиталя 1 (раскрытие неопределенностей типа 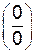). Пусть функции 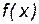, 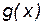определены, непрерывны и дифференцируемы в точке x₀ и некоторой ее окрестности, причем 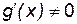для любого x из этой окрестности, и пусть 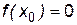, 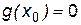(следовательно, 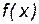, 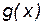– бесконечно малые при 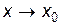). Если 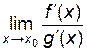существует, то существует 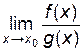и

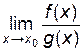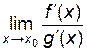= . (6.1)

Пример 6.1. Найти .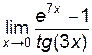

Решение.

Так как при 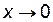функци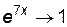и и 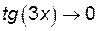, то имеем неопределенность типа 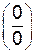. Числитель и знаменатель данной дроби непрерывны дифференцируемы и стремятся к нулю. Это означает, что можно применить правило Лопиталя:

.

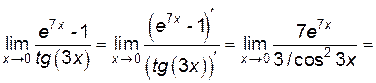
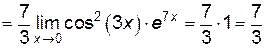Пример 6.2. Найти .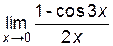

Решение.

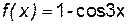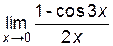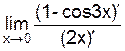
Поскольку функции , g(x)=2x удовлетворяют условиям теоремы Лопиталя, то = =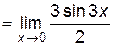0.

Замечание 1. Теорема Лопиталя справедлива и в том случае, когда функции 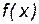, 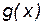не определены в точке x₀, но 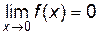и .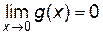

В самом деле, если доопределить 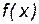, , 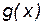положив 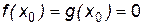, тогда 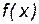, 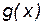будут непрерывны в точке x₀, а потому теорема Лопиталя будет применима к ним.

Замечание 2. Правило Лопиталя применимо и в том случае, когда

, .

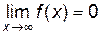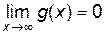Действительно, введя новую переменную 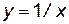, видим, что y→0 при x→¥. Тогда = = = .

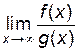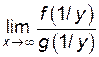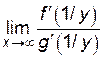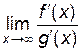Теорема Лопиталя (раскрытие неопределенностей типа ).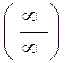

Пусть функции 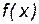, 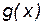дифференцируемы в окрестности точке x₀, за исключением самой точки x₀, причем 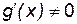, и пусть 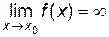, 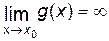. Если существует 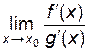то существует и 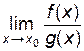, причем

= .

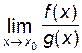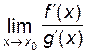Замечание 3. Предел отношения двух функций может существовать, в то время как предел отношения их производных не существует.

Например, 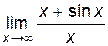=1, а 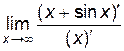= 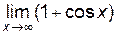– не существует, так как 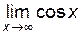не существует.

Пример 6.3. Найти .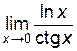

Решение.

При x → 0 и x > 0 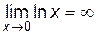, , 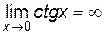следовательно, имеем отношение двух бесконечно больших при x→0 и неопределенность типа 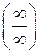. Вычислим:

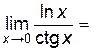
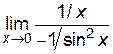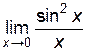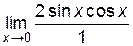= – = – = 0.

Пример 6.4. Найти .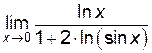

Решение.

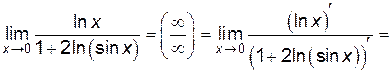
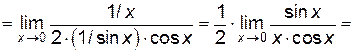
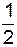
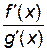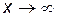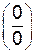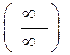Замечание 4. Если при x → x₀ ( ) является неопределенностью типа или , и 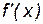, g'(x) удовлетворяют условиям теоремы Лопиталя, то

= = .

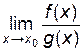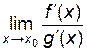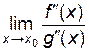Таким образом, для раскрытия неопределенностей типа 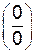или 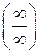иногда приходится применять правило Лопиталя несколько раз.

Замечание 5. Теорема Лопиталя остается верной и тогда, когда = .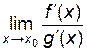

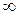Пример 6.5. Найти .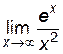

Решение.

Имеем неопределенность типа 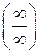. Применяя теорему Лопиталя два раза, получим: = = =¥.

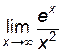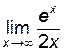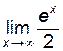Пример 6.6. Найти .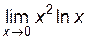

Решение.

Так как 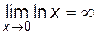, то имеем неопределенность типа (0·¥). Преобразуем ее к виду :

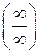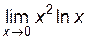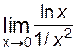= , затем применим правило Лопиталя:

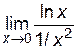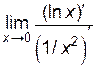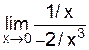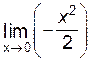= = = =0.

Итак, .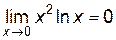

Пример 6.7. Найти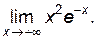

Решение.

.

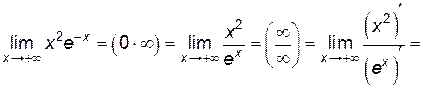
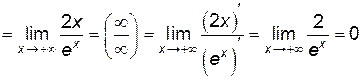Пример 6.8. Найти .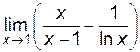

Решение.

.

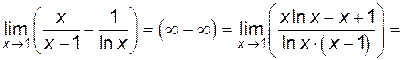
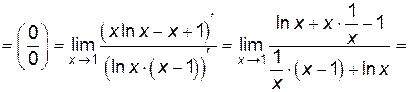
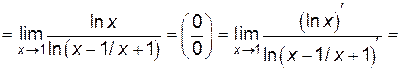
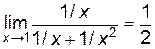Пример 6.9. Найти .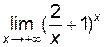

Решение.

В данном случае имеем неопределенность типа 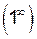, поэтому для раскрытия этой неопределенности применим метод логарифмирования.