Дифференциальные уравнения первого порядка

v Уравнение с разделяющимися переменными

Дифференциальное уравнение первого порядка называется уравнением с разделяющимися переменными, если оно может быть представлено в виде:

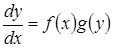(4.7)

или в виде:

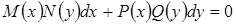(4.8)

где 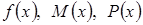- некоторые функции переменной 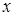; 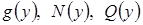- функции переменной .

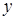Для решения такого уравнения его следует преобразовать к виду, в котором дифференциал и функции переменной 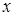окажутся в одной части равенства, а переменной 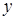- в другой. Затем проинтегрировать обе части полученного равенства.

Пример

Решить уравнение .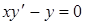

Решение.

.

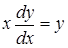Умножим обе части равенства на .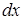

.

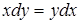Получившееся равенство разделим на .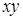

;

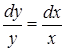откуда:

; ; ; .

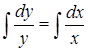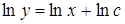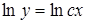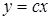v Однородные дифференциальные уравнения

Дифференциальное уравнение первого порядка называется однородным, если оно может быть представлено в виде:

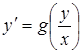, (4.9)

где 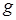- некоторая функция (одной переменной).

Понятие однородного дифференциального уравнения связано с однородными функциями. Функция 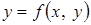называется однородной степени 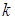, если для произвольного числа 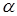выполняется равенство:

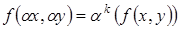(4.10)

Однородные уравнения при помощи подстановки 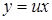приводятся к уравнениям с разделяющимися переменными.

Пример.

Решить уравнение: .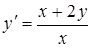

Решение.

Так как 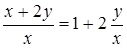, то уравнение имеет вид (4.9) при 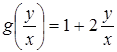. Положим 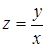, отсюда 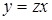и 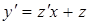. Подставим в преобразованное уравнение:

,

.

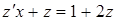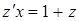Получим уравнение с разделяющимися переменными:

.

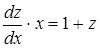Разделим обе части равенства на 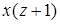и умножим на 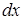( 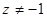, т.е. 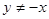, но следует отметить, что 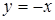является решением исходного уравнения).

.

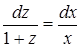Интегрируя почленно последнее равенство, получаем:

,

,

.

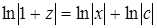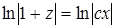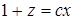Возвращаясь к первоначальным переменным, получим:

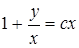, откуда 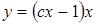( при 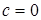получаем решение ).

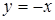v Линейные дифференциальные уравнения

Дифференциальное уравнение первого порядка называется линейным, если оно имеет вид:

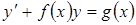(4.11)

где 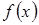и 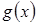- некоторые (непрерывные) функции переменной .

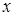Рассмотрим один из возможных способов решения уравнения: будем искать решение в виде 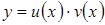, тем самым искомыми становятся функци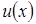и и 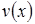, одна из которых может быть выбрана произвольно, а другая – должна определяться из уравнения (4.11). Т.е. используется в решении замена .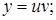

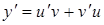Пример.

Решить уравнение: .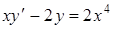

Решение.

Разделив левую и правую части на 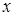приходим к линейному неоднородному уравнению:

.

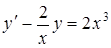Пусть 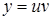, , 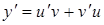тогда уравнение примет вид:

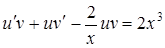или .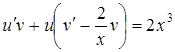

Пользуясь тем, что одну из вспомогательных функций (например 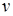) можно выбрать произвольно, подберем ее так, чтобы выражение в скобках обратилось в нуль, т.е. в качестве 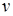возьмем одно из частных решений уравнения с разделяющимися переменными.

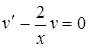или 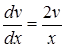; откуда: .

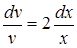Проинтегрировав, найдем какое-либо частное решение этого уравнения, например, при 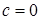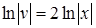, откуда .

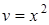При 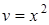исходное уравнение обратится в уравнение:

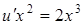или .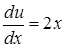

Решая это уравнение с разделяющимися переменными, получаем 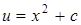. Тогда окончательно имеем:

.
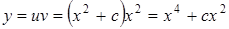