Сложение (вычитание) матриц
НЕ ВСЕ МАТРИЦЫ МОЖНО СКЛАДЫВАТЬ. Для выполнения сложения (вычитания) матриц, необходимо, чтобы они были ОДИНАКОВЫМИ ПО РАЗМЕРУ.
Например, если дана матрица «два на два», то ее можно складывать только с матрицей «два на два» и никакой другой!
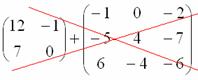
Пример:
Сложить матрицы
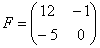 и
и 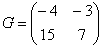
Решение: Данные матрицы имеют одинаковую размерность, поэтому их можно сложить.
Для того чтобы сложить матрицы, необходимо сложить их соответствующие элементы:
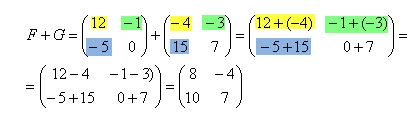
Для разности матриц правило аналогичное, необходимо найти разность соответствующих элементов.
Пример:
Найти разность матриц
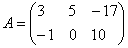 ,
, 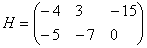
Решение: Данные матрицы имеют одинаковую размерность, поэтому можно найти их разность.
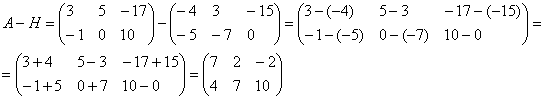
А как решить данный пример проще, чтобы не запутаться? Целесообразно избавиться от лишних минусов, для этого внесем минус в матрицу 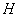 :
:
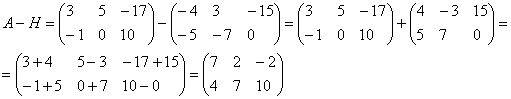
Умножение матрицы на число
Для того чтобы умножить матрицу на число, нужно каждый элемент матрицы умножить на данное число.
Пример:
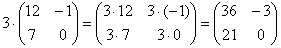
Умножение матриц
Какие матрицы можно умножать?
Чтобы матрицу 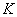 можно было умножить на матрицу
можно было умножить на матрицу 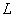 нужно, чтобы число столбцов матрицы
нужно, чтобы число столбцов матрицы 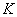 равнялось числу строк матрицы
равнялось числу строк матрицы 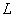 .
.
Пример:
Можно ли умножить матрицу 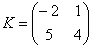 на матрицу
на матрицу 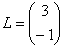 ?
?
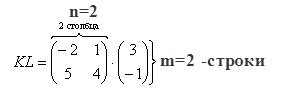
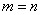 , значит, умножать данные матрицы можно.
, значит, умножать данные матрицы можно.
А вот если матрицы переставить местами, то, в данном случае, умножение уже невозможно!
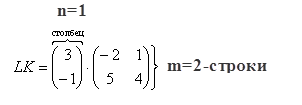
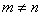 , следовательно, выполнить умножение невозможно:
, следовательно, выполнить умножение невозможно:
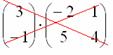
Пример.
Вычислить матрицу 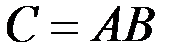 , если
, если 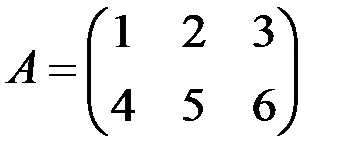 И
И 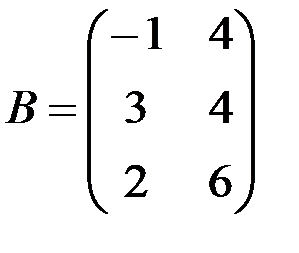 .
.
Решение: число столбцов первой матрицы то есть матрицы А равно числу строк второй матрицы В, поэтому можно найти произведение матриц А и В.
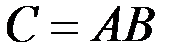 =
= 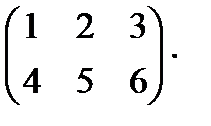
ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ
Определитель матрицы – это число, характеризующее квадратную матрицу.
! Определитель находится только для квадратной матрицы.
Определитель матрицы А обозначается: 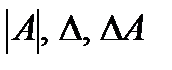 .
.
Определителем матрицы первого порядка А=(а11), или определителем первого порядка, называется элемент а11.
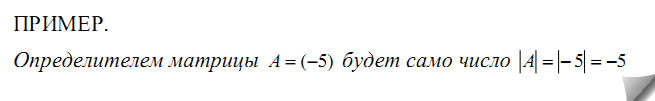
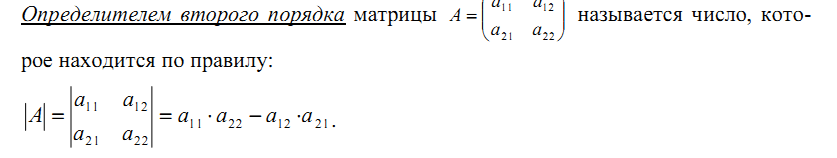
то есть определитель второго порядка равен разности произведений элементов главной диагонали и произведения элементов побочной диагоналей.



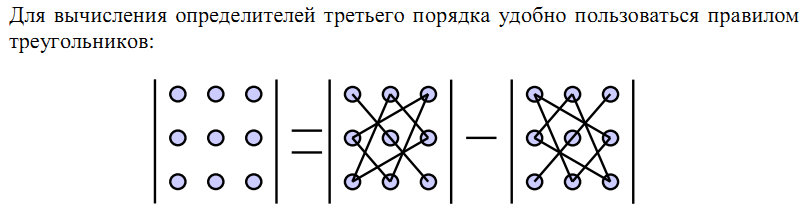 Как запомнить треугольники? Очень просто.
Как запомнить треугольники? Очень просто.
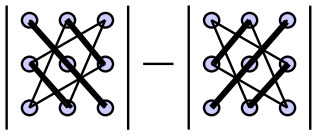

Мне же больше нравится применять правило Саррюса для нахождения определителя третьего порядка.
Правило Саррюса
Справа от определителя дописывают первых два столбца определителя и произведения элементов на главной диагонали и на диагоналях, ей параллельных, берут со знаком "плюс"; а произведения элементов побочной диагонали и диагоналей, ей параллельных, со знаком "минус":
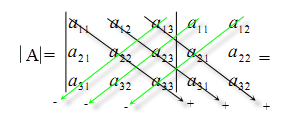
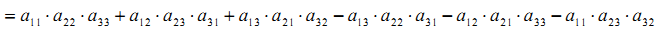

Решение: применим правило Саррюса. Для этого добавим к определителю справа первый и второй столбики.
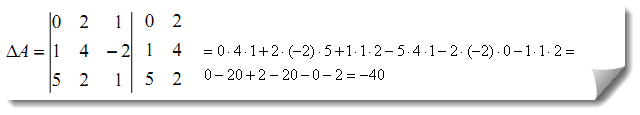
Задания для практической работы №11
Задание.
№1
Даны две матрицы A и B.
Найти:
1). Запишите матрицу D, которая получится из матрицы А (В) путём вычёркивания второго столбца и третьей строки. Найдите определитель полученной матрицы.
2). Найдите определитель матрицы А (В) по правилу а) треугольника; б)Саррюса.
3). Вычислите -2В (4А).
4). С=3A-5B;
5). 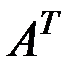 ;
;
6). BA.



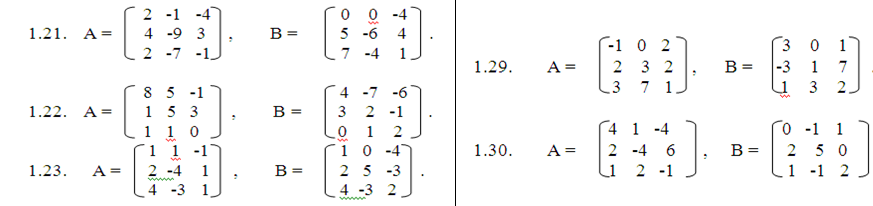
Контрольные вопросы по теме
1.Что называется матрицей?
2.Что называется матрицей-строкой, матрицей столбцом?
3.Какие матрицы называются прямоугольными, квадратными?
4.Какие матрицы называются равными?
5.Что называется главной диагональю матрицы?
6.Какая матрица называется диагональной?
7.Какая матрица называется единичной?
8.Какая матрица называется треугольной?
9.Что значит транспонировать матрицу?
10.Что называется суммой матриц?
11.Что называется произведением матрицы на число?
12.Как найти произведение двух матриц?
13.В чем состоит обязательное условие существования произведения матриц?
14.Что называется определителем матрицы?
15.Как вычислить определитель второго порядка?
16.Как вычислить определитель третьего порядка по схеме треугольников?
17.Как вычислить определитель третьего порядка по правилу Саррюса?
Практическое занятие№ 12
Тема: «Решение систем линейных алгебраических уравнений методом Крамера и методом Гаусса. Решение систем линейных алгебраических уравнений методом обратной матрицы»
Цель работы: научиться решать системы линейных уравнений методом Крамера и методом Гаусса, методом обратной матрицы
Задачи:
• развитие творческого профессионального мышления;
• познавательная мотивация;
• овладение языком науки, навыки оперирования понятиями;
• овладение умениями и навыками постановки и решения задач;
• углубление теоретической и практической подготовки;
• развитие инициативы и самостоятельности студентов.
Обеспечение практической работы:
Теоретический материал методической рекомендации к практической работе.
Учебник:
Индивидуальные карточки с вариантом практической работы.
