Основные сведения из теории. Обратная функция и ее график
Обратная функция и ее график
Если функциональная зависимость 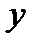 от
от 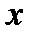 задана аналитически уравнением
задана аналитически уравнением 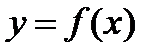 , из которого можно определить
, из которого можно определить 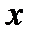 как функцию от
как функцию от 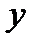 уравнением
уравнением 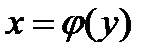 так, что каждому значению
так, что каждому значению 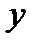 соответствует единственное значение
соответствует единственное значение 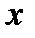 , то функция, определяемая уравнением
, то функция, определяемая уравнением 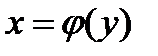 , называется обратной по отношению к функции
, называется обратной по отношению к функции 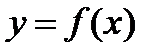 , которая в этой связи называется прямой. В уравнении
, которая в этой связи называется прямой. В уравнении 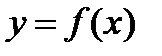 величина
величина 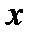 —называется переменная, а
—называется переменная, а 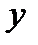 —функция. Для того чтобы сохранить стандартные обозначения, в которых
—функция. Для того чтобы сохранить стандартные обозначения, в которых 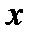 обозначает независимую переменную, а
обозначает независимую переменную, а 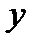 —функцию, в уравнении
—функцию, в уравнении 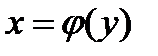 следует заменить
следует заменить 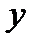 буквой
буквой 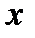 , а
, а 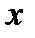 —буквой
—буквой 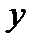 . Именно так полученную функцию
. Именно так полученную функцию 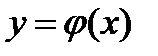 мы и будем считать обратной по отношению к функции
мы и будем считать обратной по отношению к функции 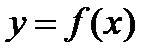 . График обратной функции
. График обратной функции 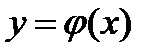 симметричен графику прямой функции
симметричен графику прямой функции 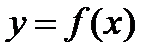 относительно биссектрисы первого и третьего координатных узлов.
относительно биссектрисы первого и третьего координатных узлов.
Задача 9.1
Найти функцию, обратную функции 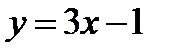 , и построить ее график.
, и построить ее график.
Решение.
Находим из данного уравнения 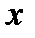 в зависимости от
в зависимости от 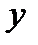 :
: 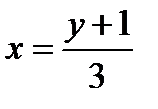 . Заменяя в этом равенстве
. Заменяя в этом равенстве 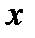 на
на 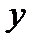 , а
, а 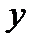 на
на 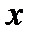 , получаем окончательно
, получаем окончательно 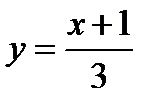 .
.
Графики заданной функции и ей обратной представлены на фиг.9.1.
Задача 9.2
Найти функцию, обратную функции 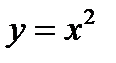
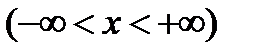 .
.
Решение.
Из уравнения 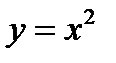 видно, что значение функции
видно, что значение функции 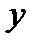 заполняют полуотрезок
заполняют полуотрезок 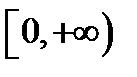 . Если это уравнение разрешить относительно
. Если это уравнение разрешить относительно 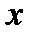 , то получим уравнение
, то получим уравнение 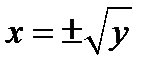 , из которого видно, что каждому значению
, из которого видно, что каждому значению 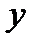 из полуотрезка
из полуотрезка 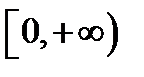 соответствует не одно, а два значения
соответствует не одно, а два значения 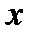 из интервала
из интервала 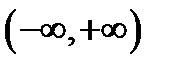 . Отсюда мы заключаем, что если функцию
. Отсюда мы заключаем, что если функцию 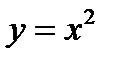 рассматривать на интервале
рассматривать на интервале 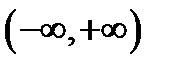 , то для ее обратной функции не существует (
, то для ее обратной функции не существует ( 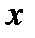 через
через 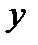 выражается не однозначно).
выражается не однозначно).
Если будем рассматривать данную функцию 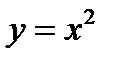 только для положительных значений
только для положительных значений 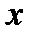 и
и 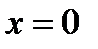 , т.е. значений
, т.е. значений 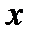 из полуотрезка
из полуотрезка 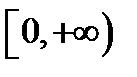 , тогда
, тогда 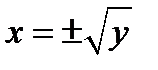 и каждому значению
и каждому значению 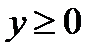 соответствует не два, а только одно значение
соответствует не два, а только одно значение 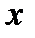 , обратная функция теперь существует и определяется уравнением
, обратная функция теперь существует и определяется уравнением 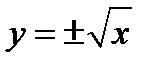 (фиг.9.2).
(фиг.9.2).
Если данную функцию 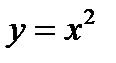 рассматривают только для значений
рассматривают только для значений 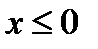 , то она и в этом случае будет иметь обратную функцию. Действительно, в этом случае
, то она и в этом случае будет иметь обратную функцию. Действительно, в этом случае 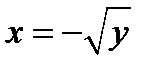 , каждому значению
, каждому значению 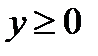 соответствует единственное значение
соответствует единственное значение 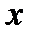 , и обратная функция определяется уравнением
, и обратная функция определяется уравнением 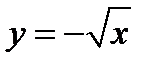 .
.
Задача 9.3
(для самостоятельного решения). Убедиться, что на интервале 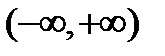 функция
функция 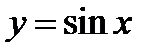 не имеет обратной функции, а на отрезке
не имеет обратной функции, а на отрезке 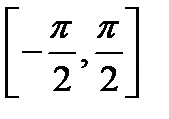 — имеет.
— имеет.
Задача 9.4
Найти функцию, обратную функции 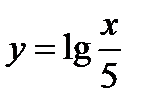
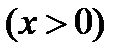 .
.
Решение.
1) Находим 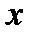 в зависимости от
в зависимости от 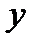 :
:
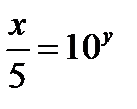 ;
; 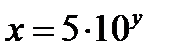 .
.
2) Заменим в последнем выражении 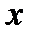 на
на 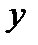 , а
, а 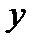 на
на 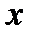 и получим
и получим 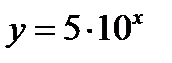 . Это и есть функция, обратная данной.
. Это и есть функция, обратная данной.
Задача 9.5
(для самостоятельного решения). Найти функции, обратные данным:
1) 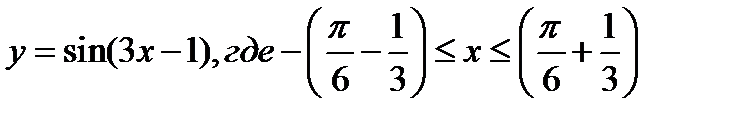 ;
;
2) 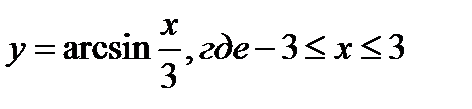 ;
;
3) 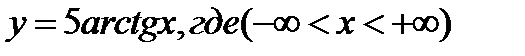 .
.
Ответ.
1) 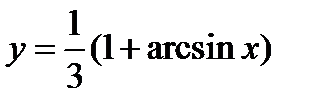 ;
;
2) 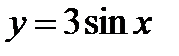 ;
;
3) 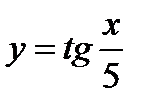 .
.
При каких значениях 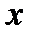 могут рассматриваться эти функции?
могут рассматриваться эти функции?
Задача 9.6
(для самостоятельного решения).Найти функцию, обратную функции 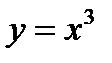 , и построить ее график, пользуясь свойством графика обратной функции.
, и построить ее график, пользуясь свойством графика обратной функции.
Задача 9.7
(для самостоятельного решения). Определить функции обратные следующим функциям:
1) 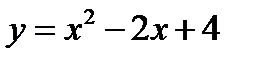 ;
;
2) 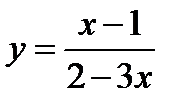 ;
;
3) 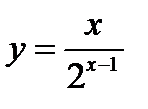 ;
;
4) 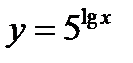 ;
;
5) 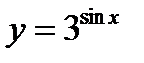 ;
;
6) 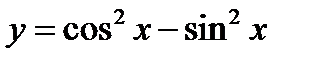 .
.
Указание. Заданную функцию рассмотреть сначала для значений 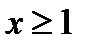 ,а потом для значений
,а потом для значений 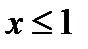 .
.
Ответ.
1) 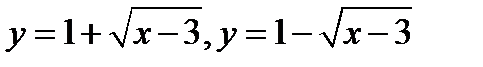
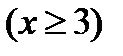 ;
;
2) 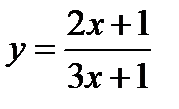 , область существования – два бесконечных интервала:
, область существования – два бесконечных интервала: 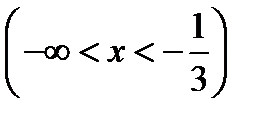 ;
; 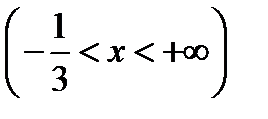 ;
;
3) 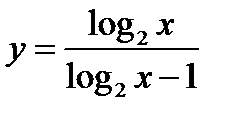 , область существования – интервалы
, область существования – интервалы 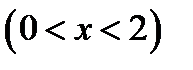 и
и 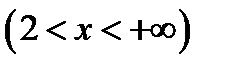
4) 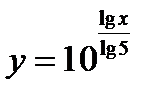 , область существования—
, область существования— 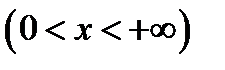 ;
;
5) 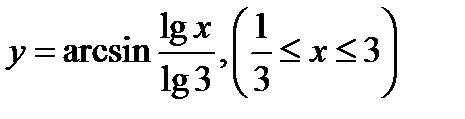 ;
;
6) 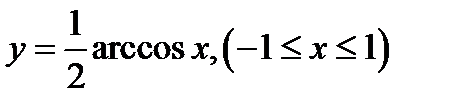 .
.
Периодические функции
