Обратная функция. сложная функция

Основные характеристики ф-ии (монотонность, четность-нечетность, периодичность)Функция, только возрастающая или только убывающая на данном числовом промежутке, называется монотонной на этом промежутке

Функция f(x) называется возрастающей на данном числовом промежутке, если большему значению аргумента соответствует большее значение функции. Функция f(x) называется убывающей на данном числовом промежутке, если большему значению аргумента соответствует меньшее значение функции.

Четные и нечетные функции

y = f (x) четная, если f (-x)=f (x) и нечетная, если f (-x)=- f (x).

Примерами четных функций являются 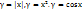и д.р

Примерами нечетных функций являются 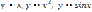и д.р

Периодическая функция ― функция, повторяющая свои значения через некоторый регулярный интервал аргумента, то есть не меняющая своего значения при добавлении к аргументу некоторого фиксированного ненулевого числа на всей области определения.

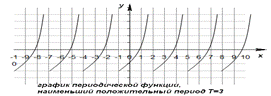
Обратная функция. Сложная функция

Пусть функция 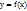строго монотонная (возрастающая или убывающая) и непрерывная на области определения 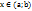, область значений этой функции 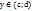, тогда на интервале 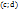определена непрерывная строго монотонная функция 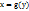с областью значений 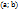, которая является обратной для 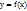. Функции f и gназывают взаимно обратными.Свойства взаимно обратных функц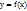ий 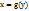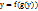. И :

• и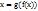
• Из первого свойства видно, что область определения функции 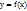совпадает с областью значений функции 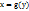и наоборот.
• Графики взаимно обратных функций симметричны относительно прямой y=x.
• Если 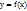возрастает, то и 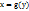возрастает, если 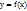убывает, то и 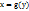убывает.

Сложная функция - это функция от функции.
Если величина y является функцией от u, то есть у = f (u), а и, в свою очередь, функцией от х, то есть u = h(х), то у - cложная функция от х, то есть y = f (h(x)), определённой для тех значений х, для которых значения h(х) входят в множество определения функции f (u). Yявляется cложная функция независимого аргумента х, а u - промежуточным аргументом.
Например, если у = u², u =sinx, то у = sin²х для всех значений х.

Основные элементарные функции и их графики. Степенные функции.

Среди огромного числа функций в ходе развития математики была выделена небольшая совокупность сравнительно простых функций, особенно часто встречающихся в самых разнообразных приложениях математического анализа и поэтому подвергнутых наиболее подробному исследованию. Их называют основными элементарными функциями.. К ним относят функции степенную, показательную и логарифмическую, тригонометрические и обратные тригонометрические функции.Степенная функция у=х^α, αєR. Примеры графиков степенных функций, соответствующих различным показателям степени, предоставлены на рисунках

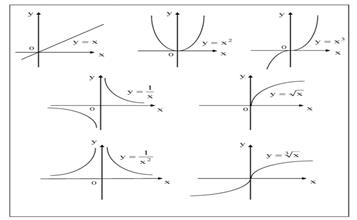
Таблица эквивалентных величин.

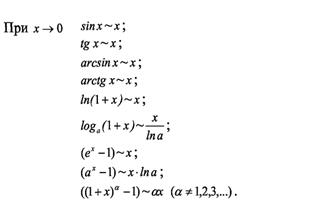17. Непрерывность функций в точке. Основные определения. Непрерывность функции на множестве Определение 1.Функция f(x) называется непрерывной в точкеa, если:1.функция f(x) определена в точке а и ее окрестности;2.существует конечный предел функции f(x) в точке a;3.этот предел равен значению функции в точке а, т.е. 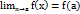Определение 2. Функция f(x) называется непрерывной в точке 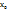, если для любого заданного числа 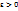можно найти такое число 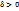(зависящее от 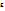и 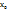), что для всех x, для которых 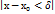, будет выполняться неравенство 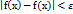Определение 3. Функция f(x) называется непрерывной в точке 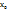, если бесконечно малому приращению аргумента 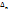соответствует бесконечно малое приращение функции 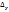, т. е. 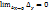. В некоторых случаях приходится пользоваться понятием односторонней непрерывности. Определение 4. Функция f(x), определенная в некоторой левой (правой) окрестности точки 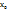, называется непрерывной слева (справа) в точке 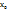, если существует предел слева (справа) функции y= f(x) и он равен 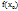. Определение 5. Функция f(x) , непрерывная во всех точках некоторого множества X, называется непрерывной на этом мно­жестве.

18. Точки разрыва функции I-го рода Определение. Точки разрыва функции I-го рода.Точка 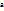, в которой нарушено хотя бы одно из трех условий непрерывности функции, а именно: Функция 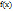определена в точке и ее окрестности;существует конечный предел функции 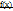в точке 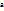;это предел равен значению функции в точке 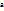, т.е. 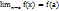называется точкой разрыва функции. Точка разрыва первого рода Определение Если в точке 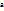существуют конечные пределы 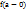и 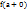, такие, что 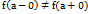, то точка 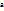называется точкой разрыва первого рода.

19. Точки разрыва функции II-го рода Определение Точка 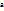, в которой нарушено хотя бы одно из трех условий непрерывности функции, а именно:

1. функция 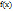определена в точке и ее окрестности;

2. существует конечный предел функции 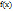в точке ;

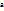3. это предел равен значению функции в точке 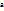, т.е.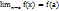

называется точкой разрыва функции.

Если хотя б один из пределов 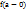или 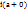не существует или равен бесконечности, то точка 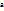называется точкой разрыва второго рода.

20. Основные теоремы о непрерывных функциях. Непрерывность элементарных функций Основные теоремы о непрерывности функциях.Теорема 1. Сумма конечного числа непрерывных функций, определенных на некотором множестве Х, есть функция непрерывная. Теорема2. Произведение конечного числа непрерывных функций есть функция непрерывная. Теорема3. Частное от деления двух непрерывных функций есть функция непрерывная во всех точках, в которых делитель отличен от нуля. Теорема 4. Непрерывная функция от непрерывной функции есть функция непрерывная. Теорема 5. Если функция у=ƒ(х) непрерывна и строго монотонна на промежутке [a;b] оси Oх, то обратная функция у=φ(х) также непрерывна и монотонна на соответствующем отрезке [c;d] оси Оу Непрерывность элементарных функций Можно доказать, что все основные элементарные функции непрерывны при всех значениях х, для которых они определены. Как известно, элементарной называется такая функция, которую можно задать одной формулой, содержащей конечное число арифметических действий и суперпозиций (операции взятия функции от функции) основных элементарных функций. Поэтому из приведенных выше теорем вытекает: всякая элементарная функция непрерывна в каждой точке, в которой она определена.

21)Производная функции. Определение производной; её механический и геометрический смысл. Производной функции y=f(x) в точке 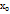называется конечный предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к 0. Функция, имеющая производную в точке 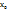, называется дифференцируемой в точке 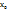. Операция нахождения производной ф-ииназ-ся дифференцированием. Скорость прямолинейного движения в материальной точке в момент времени t есть производная от пути s по времени t. Обобщая, можно сказать, что если ф-ия y=f(x) описывает какой-либо физический процесс, то производная y’ есть скорость протекания этого процесса. В этом состоит физический смысл производной. Значение производной ф-ции в точке 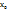равно угловому коэффициенту касательной к графику ф-ии в точке .

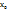22)Уравнение касательной и нормали к кривой.Как известно, из курса геометрии, уравнение прямой, проходящей через точку 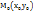с угловым коэффициентом k имеет вид y- 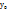=k(x- 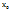), значит, уравнение касательной, проведенной к графику ф-ии y=f(x) в т. 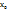можно записать в виде y – f( 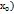= 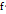( (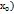x - 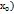. Как известно, угловые кафф. двух перпендикулярных прямых связан соотношением 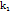= 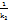, следовательно, уравнение нормали принимает вид y - f( 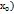= - 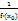(x - .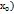

23)Связь между непрерывностью и дифференцируемостью функции. Если ф-ция дифференцируема, то она непрерывна. Обратное утверждение верно не всегда. Существуют функции, непрерывные в некоторой точке, но не имеющие в этой точке производной. Например: y = .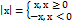

24)Производная суммы, разности, произведения и частного функции.Производная суммы двух ф-ий равна сумме производных этих ф-ий: 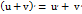. Производная разности двух ф-ий равна разности производных этих ф-ий: 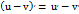. Производная произведения 2-х ф-ий равна произведению производной 1-го сомножителя на второй плюс произведение 1-го сомножителя на производную второго: 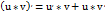. Производная частного 2-х ф-ий равна дроби, числитель которой есть разность произведений производного числителя на знаменатель дроби и числителя дроби на производную знаменателя, а знаменатель есть квадрат прежнего знаменателя: .

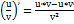25)Производная сложной и обратной функции. Рассмотрим сложную функцию y = y(u(x)). Теорема. Если функции y = y(u), u = u(x) дифференцируемы (т.е. существуют производные y'_u, u'_x), тогда сложная функция y = y(u(x)) дифференцируема и y'_x = y'_u u'_x. Рассмотрим функцию y = f(x), для которой существует обратная функция x = g(y). Теорема 5. Если обратная функция x = g(y) дифференцируема и g'(y) ≠ 0, то функция y=f(x) дифференцируема, и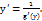

26)Дифференцирование неявных и параметрические заданных функций. Если независимая переменная x и функция y связаны уравнением вида F(x,y)=0 , которое не разрешено относительно y, то функция y называется неявной функцией переменной x.Всякую явно заданную функцию y=f(x) можно записать в неявном виде y-f(x)=0 . Обратно сделать не всегда возможно. Несмотря на то, что уравнение F(x,y)=0 не разрешимо относительно y, оказывается возможным найти производную от y по x. В этом случае необходимо продифференцировать обе части заданного уравнения, рассматривая функцию yкак функцию от x, а затем из полученного уравнения найти производную y’ . Предположим, что функциональная зависимость y от x не задана непосредственно y=f(x), а через промежуточную величину —t .Тогда формулы 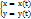задают параметрическое представление функции одной переменной. Пусть функция 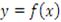задана параметрическими уравнениями 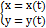где t – параметр. Тогда производная этой функции по переменной x равна отношению производных 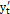и 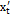по параметру t: 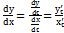Равнениями 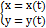где t – параметр. 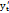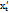Тогда производная этой функции по переменной x равна отношению производных и по параметру 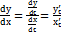t:

Дифференциал функции.

Главная линейная относительно ∆х часть приращения ф-ии, отличная от самого приращения на б.м.в. более высокого порядка, чем ∆х, называется дифференциалом ф-ии. Обозначается дифференциал dy. dy = 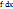, где dx=∆х.

Таблица дифференциалов.

1.

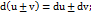
2.

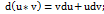
3.

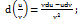
4.

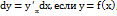
5.

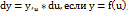
6. ;

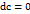7.

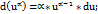
8.

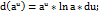
9.

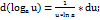
10.

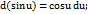
11.

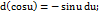
12.

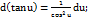
13.

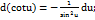
14.

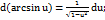
15.

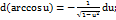
16.

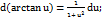
17.

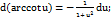
{\displaystyle ~d^{n}z=d(d^{n-135:Некоторые теоремы о дифференцируемых функциях.

Рассмотрим ряд теорем, имеющих большое теоретическое и прикладное значение.

Теорема Ролля: Если функция 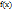непрерывна на отрезке 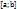, дифференцируема на интервале 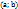и на концах отрезка принимает одинаковые значения 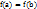, то найдется хотя бы одна точка 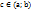, в которой производная 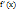обращается в нуль, то есть 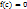. Теорема Коши: Если функция 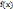и 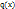непрерывны на отрезке 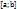, дифференцируемы на интервале 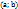, причем 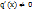для 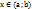, то найдется хотя бы одна точка 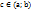такая, что выполняется равенство .

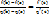Теорема Лагранжа: Если функция 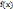непрерывна на отрезке 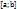, дифференцируема на интервале 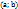, то найдется хотя бы одна точка 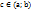такая, что выполняется равенство .

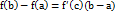36: Правила Лопиталя. Теорема( Правило Лопиталя раскрытия неопределенностей вида ) . Пусть функци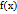и и 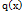непрерывны и дифференцируемы в окрестности точки 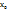и обращаются в нуль в этой точке: 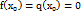. Пусть 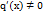в окрестности точки 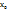. Если существует предел 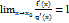, то

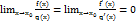
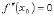либо 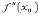не существует. Теорема (Правило Лопиталя раскрытия неопределенностей вида ). Пусть функция 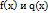непрерывны и дифференцируемы в окрестности точки , в этой окрестности 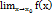= 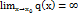, 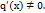Если существует предел 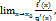то 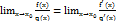. Правило Лопиталя применяется для раскрытия неопределенностей вида и , которые называют основными.

(Правило Лопиталя).

Пусть функци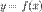и и 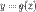удовлетворяют следующим условиям:

1) эти функции дифференцируемы в окрестности точки 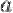, кроме, может быть, самой точки ;

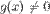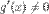2) и в этой окрестности;

3) ;

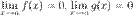4) 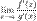существует конечный или бесконечный.

Тогда существует и 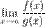, причем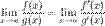

39. Первое и второе достаточные условия существования экстремума. Если непрерывная функция 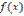дифференцируема в некоторой δ-окрестности критической точки 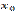и при переходе через нее (слева направо) производная 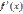меняет знак с плюса на минус, то 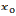есть точка максимума; с минуса на плюс - то 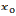есть точка минимума. Доказательство: Рассмотрим -окрестность точки 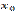. Пусть 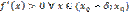и 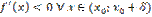. Тогда функция 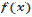возрастает на интервале 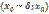, а на интервале 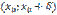она убывает. Отсюда следует, что значение 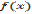в точке 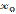является наибольшим на интервале 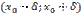, т.е. 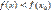для всех 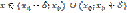. Следовательно 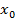есть точка максимума. Второе достаточное условие:Если в точке 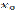первая производная функции 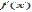равна нулю ( 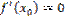), а вторая производная в точке 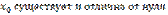( 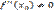), то при 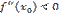в точке 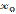функция имеет максимум, а при 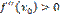– минимум. Доказательство: Пусть 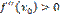Т.к. 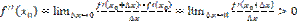, то 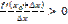в достаточно малой окрестности точки 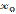. Если 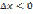, то 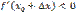, если 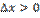, то 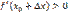. Из этого следует, что при переходе через точку 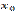первая производная меняет знак с минуса на плюс. Следовательно 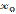есть точка минимума.

Асимптоты графика функции.

Назовём асимптотами прямые линии, к которым неограниченно приближается график функции, когда точка графика неограниченно удаляется от начала координат. В зависимости от поведения аргумента при этом, различают вертикальные, наклонные и горизонтальные асимптоты.

Вертикальной асимптотой графика функции y=f(x) называется вертикальная прямая 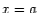, если lim (x→a) f(x)=∞ или lim (x→a+0) f(x)=∞, или lim (x→a-0) f(x)=∞.

Наклонной асимптотой графика функции y=f(x) при x→+∞ называется прямая y=kx+b, если выполнены два условия: 1) некоторый луч (a; +∞) целиком содержится в D(f); 2) расстояние по вертикали между графиком и прямой стремится к 0 при x→+∞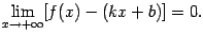

Наклонной асимптотой графика функции y=f(x) при x→ - ∞ называется прямая y=kx+b, если выполнены два условия: 1) некоторый луч (-∞; a) целиком содержится в D(f); 2) расстояние по вертикали между графиком и прямой стремится к 0 при x→ - ∞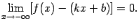

В случае, если наклонная асимптота расположена горизонтально, то есть при k=0, она называется горизонтальной асимптотой. Таким образом, горизонтальная асимптота -- частный случай наклонной асимптоты; прямая y=c=const является горизонтальной асимптотой графика y=f(x) при x→+∞ или x→-∞, ес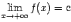ли или 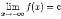соответственно.
45. Общая схема исследования функции и построения графика.

Исследование функции у = f (х) целесообразно вести в определенной последовательности.

1. Найти область определения функции.

2. Найти (если это можно) точки пересечения графика с осями координат.

3. Найти интервалы знакопостоянства функции (промежутки, на Которых f(х) > 0 или f(х) < 0).

4. Выяснить, является ли функция четной, нечетной или общего Ища.

5. Найти асимптоты графика функции.

6. Найти интервалы монотонности функции.

7. Найти экстремумы функции.

8. Найти интервалы выпуклости и точки перегиба графика функ­ции.

9. На основании проведенного исследования построить график функ­ции. Заметим, что приведенная схема исследования не является обя­зательной.
46. Понятие неопределенного интеграла.

Неопределенным интегралом от функции f(x) называется совокупность всех ее первообразных.

Если функция F(x) является первообразной ф-ии f(x) на (a,b), то множество всех первооб-х для f(x) задается формулой F(x)+C, где С-постоянное число.

Множество всех первооб-х ф-ий F(x)+C для f(x) наз-ся неопределенным интегралом от ф-ии f(x) и обозначается символом ∫f(x)dx. Таким образом, по определению ∫f(x)dx=F(x)+C.

Операция нахождения неопределенного интеграла от ф-ии наз. интегрированием этой ф-ии.

Таблица основных неопределенных интегралов.

Ряды Тейлора и Маклорена.

Если функция f (x) имеет непрерывные производные вплоть до (n+1)-го порядка, то ее можно разложить в степенной ряд по формуле Тейлора:

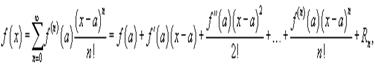
где R_n − остаточный член в форме Лагранжа определяется выражением

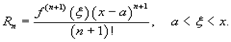Если приведенное разложение сходится в некотором интервале x, т.е. 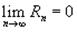, то оно называется рядом Тейлора, представляющим разложение функции f (x) в точке a.

Если a = 0, то такое разложение называется рядом Маклорена:

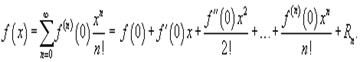
86. Разложение в ряд функций Маклорена ln (1+x), cos x.

Применим интегральную формулу 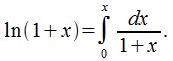Разложение 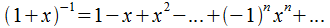может быть осуществлено при m=-1 В этом случае

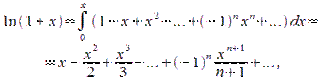
при этом для ряда характерна абсолютная расходимость на промежутке(-1,1)Если, x=-1получаем, 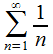что представляет собой гармонический расходящийся ряд, при 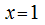ряд 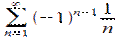предполагает условную сходимость. В соответствии с формулой 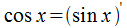, запишем ряд для cos x почленным дифференцированием: 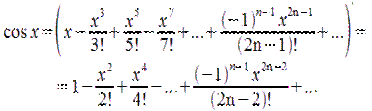Для ряда характерна абсолютная сходимость на интервале (-∞,+∞). Функция y=e^x. Ряд Маклорена имеет вид .

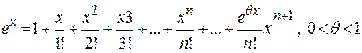Найдем радиус сходимости ряда .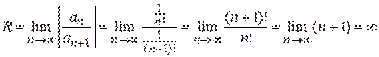

Область сходимости ряда . (-∞,+∞)

87. Разложение в ряд Маклорена 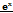,sinx.

Функция y=sin x . Ряд Маклорена имеет вид 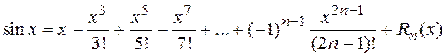, где 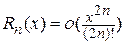- остаточный член, записанный в данном случае в форме Пеано. Запись 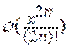означает, что функция 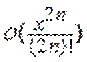является бесконечно малой по сравнению с функцией 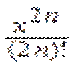. Найдем радиус сходимости этого ряда 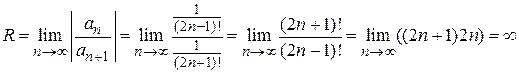. Область сходимости ряда .

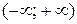Дифференциальные уравнения. Основные понятия.

Дифференциальное уравнение — уравнение, связывающее значение производной функции с самой функцией, значениями независимой переменной, числами (параметрами). Порядок входящих в уравнение производных может быть различен (формально он ничем не ограничен). Производные, функции, независимые переменные и параметры могут входить в уравнение в различных комбинациях или все, кроме хотя бы одной производной, отсутствовать вовсе. Дифференциальное уравнение порядка выше первого можно преобразовать в систему уравнений первого порядка, в которой число уравнений равно порядку исходного уравнения. Все дифференциальные уравнения можно разделить на обыкновенные (ОДУ), в которые входят только функции (и их производные) от одного аргумента, и уравнения с частными производными (УРЧП), в которых входящие функции зависят от многих переменных. Существуют также стохастические дифференциальные уравнения (СДУ), включающие случайные процессы.

Основные характеристики ф-ии (монотонность, четность-нечетность, периодичность)Функция, только возрастающая или только убывающая на данном числовом промежутке, называется монотонной на этом промежутке

Функция f(x) называется возрастающей на данном числовом промежутке, если большему значению аргумента соответствует большее значение функции. Функция f(x) называется убывающей на данном числовом промежутке, если большему значению аргумента соответствует меньшее значение функции.

Четные и нечетные функции

y = f (x) четная, если f (-x)=f (x) и нечетная, если f (-x)=- f (x).

Примерами четных функций являются 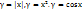и д.р

Примерами нечетных функций являются 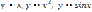и д.р

Периодическая функция ― функция, повторяющая свои значения через некоторый регулярный интервал аргумента, то есть не меняющая своего значения при добавлении к аргументу некоторого фиксированного ненулевого числа на всей области определения.

Обратная функция. Сложная функция

Пусть функция 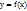строго монотонная (возрастающая или убывающая) и непрерывная на области определения 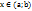, область значений этой функции 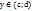, тогда на интервале 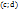определена непрерывная строго монотонная функция 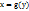с областью значений 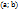, которая является обратной для 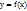. Функции f и gназывают взаимно обратными.Свойства взаимно обратных функц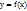ий 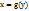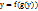. И :

• и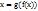
• Из первого свойства видно, что область определения функции 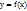совпадает с областью значений функции 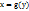и наоборот.
• Графики взаимно обратных функций симметричны относительно прямой y=x.
• Если 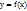возрастает, то и 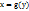возрастает, если 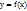убывает, то и 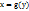убывает.

Сложная функция - это функция от функции.
Если величина y является функцией от u, то есть у = f (u), а и, в свою очередь, функцией от х, то есть u = h(х), то у - cложная функция от х, то есть y = f (h(x)), определённой для тех значений х, для которых значения h(х) входят в множество определения функции f (u). Yявляется cложная функция независимого аргумента х, а u - промежуточным аргументом.
Например, если у = u², u =sinx, то у = sin²х для всех значений х.