Линейные однородные дифференциальные уравнения II порядка с постоянными коэффициентами
Дифференциальное уравнение называется линейным, если оно имеет вид 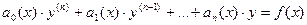 . Если в нем функция в правой части принимает нулевой значение, т.е.
. Если в нем функция в правой части принимает нулевой значение, т.е. 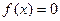 , то уравнение называют однородным.
, то уравнение называют однородным.
Линейное однородное уравнение II порядка с постоянными коэффициентами имеет вид 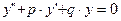 , где p и q – действительные числа. Его решение ищется в виде
, где p и q – действительные числа. Его решение ищется в виде 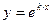 , где k – постоянная, подлежащая определению.
, где k – постоянная, подлежащая определению.
Если 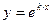 , то
, то 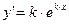 ,
, 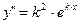 . Подстановка полученных выражений в уравнение и сокращение на
. Подстановка полученных выражений в уравнение и сокращение на 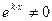 приводит к квадратному уравнению
приводит к квадратному уравнению 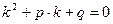 относительно k. Оно называется характеристическим уравнением исходного дифференциального уравнения с корнями
относительно k. Оно называется характеристическим уравнением исходного дифференциального уравнения с корнями 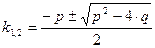 . Возможно 3 случая.
. Возможно 3 случая.
1) Числа 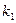 и
и 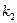 действительны и различны, т.е.
действительны и различны, т.е. 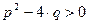 . Тогда
. Тогда 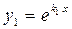 ,
, 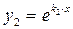 , а общее решение исходного уравнения есть линейная комбинация полученных, т.е.
, а общее решение исходного уравнения есть линейная комбинация полученных, т.е. 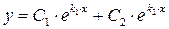 .
.
2) Числа 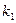 и
и 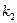 равны, т.е.
равны, т.е. 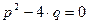 . Тогда
. Тогда 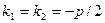 , а общее решение исходного уравнения имеет вид
, а общее решение исходного уравнения имеет вид 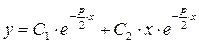 .
.
3) Числа 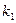 и
и 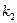 - комплексно-сопряженные, т.е.
- комплексно-сопряженные, т.е. 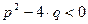 . Обозначим
. Обозначим 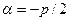 ,
, 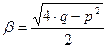 , поскольку
, поскольку 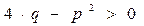 . Тогда общее решение исходного дифференциального уравнения имеет вид
. Тогда общее решение исходного дифференциального уравнения имеет вид 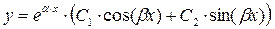 .
.
Линейные неоднородные дифференциальные уравнения II порядка с постоянными коэффициентами
Теорема. Общее решение неоднородного дифференциального уравнения II порядка с постоянными коэффициентами вида 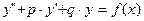 является суммой общего решения соответствующего однородного уравнения
является суммой общего решения соответствующего однородного уравнения 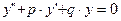 и частного решения данного неоднородного уравнения.
и частного решения данного неоднородного уравнения.
Поскольку метод нахождения общего решения однородного уравнения рассмотрен ранее, рассмотрим вопрос нахождения частного решения неоднородного уравнения в зависимости от вида функции 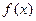 в его правой части.
в его правой части.
1) 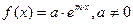
Частное решение ищется в виде 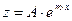 , где
, где 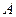 - неопределенный коэффициент. Тогда
- неопределенный коэффициент. Тогда 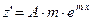 ,
, 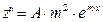 . После подстановки в исходное уравнение и сокращения на
. После подстановки в исходное уравнение и сокращения на 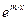 получим
получим 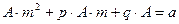 , откуда
, откуда 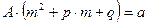 . Возможно 3 случая.
. Возможно 3 случая.
а) уравнение 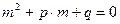 не имеет действительных корней, тогда
не имеет действительных корней, тогда 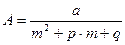 ;
;
б) уравнение 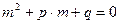 имеет два различных действительных корня, тогда частное решение следует искать не в виде
имеет два различных действительных корня, тогда частное решение следует искать не в виде 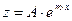 , а в виде
, а в виде 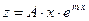 ;
;
в) уравнение 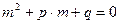 имеет два одинаковых действительных корня, тогда частное решение следует искать не в виде
имеет два одинаковых действительных корня, тогда частное решение следует искать не в виде 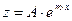 , а в виде
, а в виде 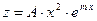 .
.
2) 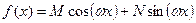
Частное решение ищется в виде 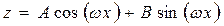 , где
, где 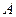 и
и 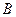 – неопределенные коэффициенты.
– неопределенные коэффициенты. 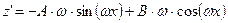 ,
, 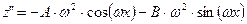 . После подстановки в исходное уравнение получим
. После подстановки в исходное уравнение получим 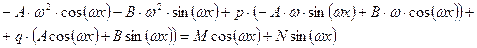
Перегруппировав слагаемые с косинусами и синусами, получим
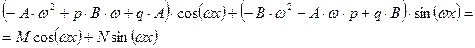 .
.
Приравнивая коэффициенты при синусе и косинусе в правой и левой частях уравнения, получим систему из двух уравнений относительно 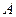 и
и 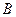 :
:
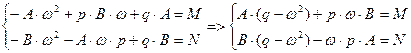 .
.
Единственная ситуация, когда полученная система несовместна – это 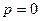 ,
, 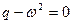 . Тогда частное решение ищется в виде
. Тогда частное решение ищется в виде 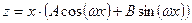 . Во всех остальных случаях решение полученной системы дает искомые значения
. Во всех остальных случаях решение полученной системы дает искомые значения 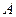 и
и 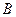 .
.
3) 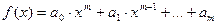
а) если 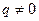 , то частное решение имеет вид
, то частное решение имеет вид 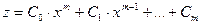 ;
;
б) если 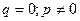 , то частное решение имеет вид
, то частное решение имеет вид 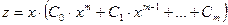 ;
;
в) если 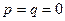 , то частное решение имеет вид
, то частное решение имеет вид 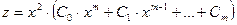 .
.
