Мұндағы -бірінші сымдағы ток бойынша берілген магнит өрісінің кернеулік векторы. 1 страница
Азақстан Республикасының білім және ғылым министрлігі
Алматы энергетика және байланыс институты
М.М.Аршидинов.
Электротехниканың теориялық негіздері
Оқу құралы
Алматы 2003
УДК 621.3 (0.75)
Электротехниканың теориялық негіздері:
Оқу құралы/Аршидинов.М.М.
АЭжБИ ,Алматы 2000.- 78 бет.
Оқулықта толық шығару жолдарымен және түсіндірулерімен типтік есептер, тұрақты және айнымалы ережедегі электр тізбектерінің негізгі есептеу әдістерінің қолдануының мысалдары, электростатикалық өріс, және тұрақты тоқтағы магнит өрісі бойынша негізгі типтегі есептердің мысалдары берілген.
Жоғары оқу орындарының электротехникалық және электроэнергетикалық мамандық студенттеріне арналған.
Кесте. 3,Ил 52, библиогр.10 аталу.
РЕЦЕНЗЕНТ: ААА-сынын электротехника жене радиотехника кафедранын менгерушici техника гылымынын кандидаты, профессор У.И.Медеуов.
Қазақстан Республикасының білім және ғылым министірлігінің 2000 жылғы жоспары бойынша басылған.
ISBN-9905-494-84-3
Алматы Энергетика және байланыс институты , 2003
Кіріспе
Электротехниканың теориялық негіздері жоғары оқу орындарының электротехникалық және электроэнергетикалық мамандықтарының негізгі пәндерінің тірегі және алғашқы базалық курсы болып табылады. Жаңа оқу жоспарына байланысты ЭТН курсы 2 семестр бойы оқытылады. Осыған байланысты студенттердің өзіндік жұмыстарының көлемі едәуір үлкейтілген (жалпы сағат санының 60 процентіне деін)және есептеу графикалық жұмыстарының саны көбейтілген.
Оқу құралының мақсаты студенттердің өзіндік жұмыстарына көмек беру. Сол себептен барлық есептер толық шығару жолдарымен, түсіндірмелерімен, методикалық нұсқауларымен берілген және соған байланысты теориялары мен есептеу формулалары көрсетілген.
Оқу құралының тұрақты тоқ тізбек мысалында электр тізбектерінің негізгі есептеу әдістерінің қолданылуы қарастырылған, бір фазалық синусоидалық тоқтың тармақталған тізбегінің және симметриялық және аппаты ережелердегі статикалық жүктемесі бар үш фазалық тізбектердің есептеутеулері көрсетілген. Симметриялық әдістегі есептеуге құраушы динамикалық жүктемесі бар үш фазалық тізбектің синусоидалы емес тоқтағы және кернеудегі есептеу ерекшеліктері қарастырылған. Классикалық және операторлық әдіспен сызықты электр тізбектерінің өтпелі процестерінің талдауларының мысалдары берілген, жоғары вольтті электр беріліс желілері мысалында таралған параметрлі тізбектердің есептеулері көрсетілген.
Құрамының әр түрлі қасиеттерімен зарядталған өткізгіштер жүйесіндегі электростатикалық есептеу сұрақтары, өткізгіштік ортадағы электр өрістерінің және тұрақты тоқты магнит өрістерінің есептеулері қарастырылған.
1.Тұрақты тоқтың электр тізбектерін есептеу
Тұрақты тоқтың сызықты электр тізбектерін есептеу Ом және Кирхгоф заңдарының қолдануларына негізделген. (1.1-сурет) электр тізбегінің мысалындағы есептеуді қарастырайық.
Берілгені:Э.Қ.К. E 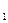 =10B, E
=10B, E 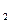 =20B, E
=20B, E 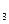 =5B, E
=5B, E 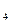 =15B, E
=15B, E 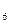 =10B. Тоқ көзінің тоғы J
=10B. Тоқ көзінің тоғы J 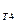 =2A.
=2A.
Электр тізбектің тармақтарының кедергілері:R 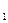 =2Ом, R
=2Ом, R 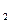 =4Ом, R
=4Ом, R 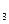 =3Ом, R
=3Ом, R 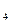 =5Ом, R
=5Ом, R 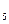 =2Ом, R
=2Ом, R 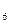 =4Ом.
=4Ом.
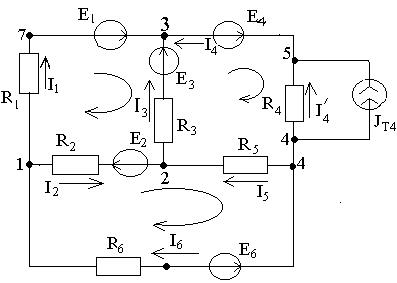 |
1.1- сурет
1.1 Кирхгоф заңын негіздеп электр тізбек схемасының барлық тармақтарындағы тоқты есептеу үшін теңдеу құру.
Электр тізбектің (1.1-сурет) схемасындағы барлық тармақтарындағы тоқтарға оң кез- келген бағыттарын таңдаймыз.
Кирхгофтың бірінші заңы бойынша теңдеулер жазамыз. Кирхгофтың бірінші заңы электр тізбектің схемасындағы түйіндерге қолданылады және былай тұжырымдалады:
Түйіндегі тоқтардың алгебралық қосындысы нөлге тең.
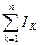 =0
=0
Кирхгоф заңы бойынша құрастырылатын теңдеулер саны түйін санынан бірді алғанға тең болады
Схема үшін (1.1- сурет) түйін саны N=5,
Теңдеулер саны Y=N 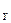 -1=5-1=4
-1=5-1=4
Түйінге бағытталған тоқтарды теріс таңбамен, түйіннен бағытталған тоқтарды оң таңбамен жазамыз.
I 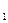 +I
+I 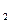 -I
-I 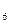 =0 (1- түйіні үшін);
=0 (1- түйіні үшін);
-I 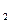 +I
+I 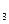 -I
-I 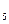 =0 (2- түйіні үшін); (1.1)
=0 (2- түйіні үшін); (1.1)
-I 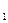 -I
-I 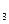 -I
-I 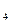 =0 (3-түйіні үшін);
=0 (3-түйіні үшін);
I 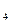 -I
-I 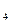 -J
-J 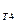 =0 (5-түйіні үшін).
=0 (5-түйіні үшін).
Кирхгофтың екінші заңына теңдеулер жазайық.
Кирхгофтың екінші заңы электр тізбектің схемасының контурларына қолданылады және келесі түрмен тұжырымдалады: кез-келген тұйық контурда осы контурға кіретін кедергілердегі кернеулердің алгебралық қосындысы Э.Қ.К.-ң алгебралық қосындысына тең.
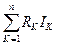 =
= 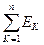
Өзара тәуелсіз контурларды таңдаймыз. Контурлар өзара тәуелсіз, егер теңдеу құрылған әрбір келесі контурда ең болмағанда бір жаңа тармақ болса және жалпы тармақтарды жою жолымен теңдеулер жазылған контурлардан шықпайтын болса, контур құрамында идеал тоқ көзі бар тармақ болмауы керек.
Контурлардың айналу бағыттарын кез-келген бағытта аламыз.
Контурдың таңдап алынған айналу бағыты тоқтар мен Э.Қ.К.-ң оң бағытымен сәйкес келсе, тоқтар мен Э.Қ.К.-ң бағыты оң таңбамен алынады. Контурдың таңдап алынған айналу бағыты тоқтар мен Э.Қ.К.-ң бағытына қарама-қарсы болса, тоқтар мен Э.Қ.К.-ң бағыты теріс таңбамен алынады.
Кирхгофтың екінші заңы бойынша құрастырылған теңдеулер саны мынаған тең:
k=N 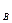 -N
-N 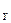 -Y , мұндағы N
-Y , мұндағы N 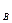 –тармақтар саны, N
–тармақтар саны, N 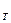 - тоқ көзі бар тармақтар саны.
- тоқ көзі бар тармақтар саны.
k=8-1-4=3
R 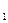 I
I 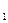 -R
-R 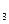 I
I 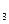 -R
-R 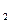 I
I 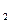 =E
=E 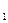 -E
-E 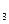 +E
+E 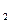 (1-3-2-1 контуры үшін);
(1-3-2-1 контуры үшін);
R 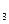 I
I 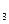 -R
-R 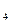 I
I 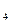 ’+R
’+R 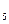 I
I 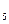 =E
=E 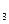 +E
+E 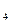 (2-3-5-4-2 контуры үшін); (1.2)
(2-3-5-4-2 контуры үшін); (1.2)
R 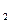 I
I 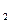 -R
-R 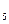 I
I 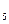 +R
+R 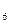 I
I 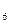 =-E
=-E 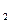 -E
-E 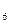 (1-2-4-1 контуры үшін).
(1-2-4-1 контуры үшін).
1.2 Контурлық тоқтар әдісімен электр тізбегінің схемасындағы ,барлық тармақтардағы тоқтарды есептеу.
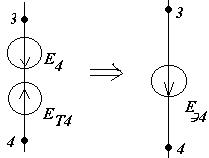
J 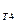 -тоқ көзін E
-тоқ көзін E 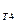 Э.Қ.К-ң эквивалент көзімен алмастырайық.
Э.Қ.К-ң эквивалент көзімен алмастырайық.
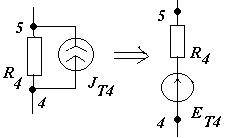 |
E
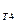 =R
=R 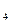 J
J 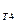 =5·2=10B
=5·2=10B Е 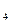 және Е
және Е 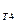 Э.Қ.К.–ң көздерін, Е
Э.Қ.К.–ң көздерін, Е 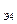 бір эквиваленттік көзімен алмастырамыз.
бір эквиваленттік көзімен алмастырамыз.
 |
Е 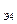 =E
=E 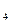 -E
-E 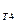 =15-10=5B
=15-10=5B
(1.2-сурет) Электр тізбегі үшін контурлық тоқтар әдісі бойынша тоқтарды есептеу үшін теңдеу құраймыз.
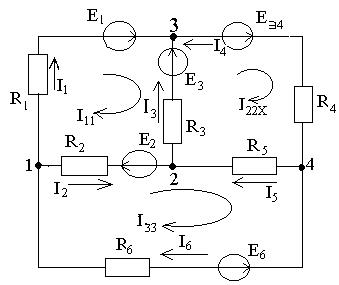 |
Сурет1.2
Өзара тәуелсіз контурларды таңдап аламыз және олардың әр қайсысында бір тоқ тұйықталуы қажет. Контурлық тоқтардың оң бағыттарын қалауымызша аламыз. К.Т.Т. бойынша құрастырылған теңдеулер саны Кирхгофың екінші заңы бойынша жазылған теңдеулер санына тең болады.
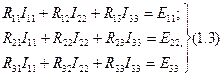
R 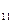 ,R
,R 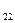 ,R
,R 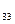 – контурлардың меншікті кедергілері.
– контурлардың меншікті кедергілері.
Контурдың меншікті кедергісі осы контурға кіретін тармақтардың кедергілерінің қосындысына тең:
R 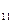 =R
=R 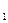 +R
+R 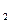 +R
+R 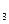 =2+4+3=9 Ом;
=2+4+3=9 Ом;
R 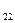 =R
=R 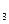 +R
+R 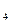 +R
+R 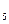 =3+5+2=10 Ом;
=3+5+2=10 Ом;
R 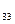 =R
=R 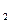 +R
+R 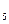 +R
+R 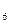 =4+2+4=10 Ом.
=4+2+4=10 Ом.
R 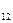 =R
=R 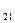 ;R
;R 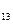 =R
=R 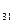 ;R
;R 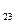 =R
=R 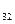 – контурдың жалпы кедергілері.
– контурдың жалпы кедергілері.
Контурлардың жалпы кедергісі, осы контурларға ортақ тармақтың кедергісіне тең. Қарастырылатын контурлардың контурлық тоқтары осы контурларға ортақ тармақтың бағытымен бір бағытта болса, жалпы кедергі “+” таңбасыменалынады, жалпы тармақтардағы контурлық тоқтар қарама-қарсы бағытта болса, “-“ таңбамен алынады.
R 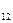 =R
=R 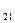 =-R
=-R 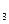 =-3 Ом;
=-3 Ом;
R 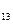 =R
=R 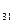 =-R
=-R 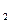 =-4 Ом;
=-4 Ом;
R 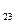 =R
=R 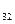 =-R
=-R 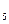 =-2 Ом.
=-2 Ом.
E 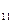 , E
, E 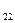 , E
, E 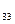 – контурлық Э.Қ.К.
– контурлық Э.Қ.К.
Әрбір контурлық Э.Қ.К. осы контурға кіретін барлық тармақтардағы Э.Қ.К.-ң алгебралық қосындысысына тең. Берілген контурда тұйықталатын контурлық тоқтың оң бағытымен сәйкес келетін Э.Қ.К.-ң оң бағыттары оң таңбамен алынады.
E 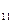 =E
=E 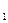 -E
-E 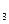 +E
+E 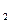 =10-5+20=25B;
=10-5+20=25B;
E 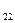 =E
=E 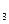 +E
+E 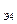 =5+5=10B;
=5+5=10B;
E 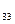 =-E
=-E 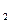 -E
-E 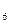 =-20-10=-30B.
=-20-10=-30B.
Контурлық тоқтар тәсілі бойынша тоқтарды есептеудің теңдеулер жүйелері келесі түрде болады.



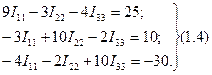
Анықтауыштар арқылы (1.4) жүйені шешіп, I 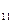 ,I
,I 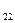 ,I
,I 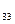 тоқтарын анықтаймыз.
тоқтарын анықтаймыз.
Жүйенің 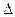 анықтауышын есептейміз:
анықтауышын есептейміз:
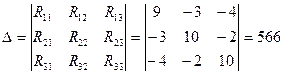
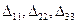 анықтауыштарын есептейиіз:
анықтауыштарын есептейиіз:
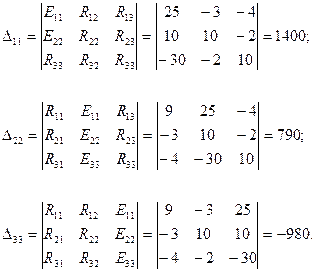
Контурлық тоқтарды формулалар арқылы анықтаймыз;
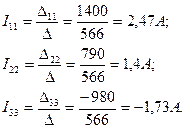

 Электр тізбектің тармақтарындағы тоқтарды есептейміз.
Электр тізбектің тармақтарындағы тоқтарды есептейміз.
Тармақтардағы I 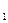 ,I
,I 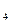 ,I
,I 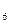 тоқтар контурлық тоқтарға тең;
тоқтар контурлық тоқтарға тең;
I 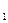 =I
=I 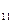 =2,47A;
=2,47A;
I 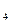 =-I
=-I 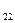 = -1,4A;
= -1,4A;
I 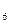 =I
=I 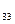 = -1,73A.
= -1,73A.
Бірнеше контурларға ортақ тармақтардағы I1,I3,I5 тоқтары осы тармақтардан өтетін контурлық тоқтардың алгебралық қосындысына тең;
I 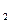 =-I
=-I 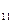 +I
+I 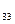 =-2,47-1,73= -4,2A;
=-2,47-1,73= -4,2A;
I 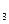 =I
=I 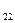 -I
-I 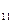 =1,40+2,47= -1,07A;
=1,40+2,47= -1,07A;
I 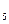 =I
=I 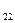 -I
-I 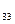 =1,40+1,73=3,13A.
=1,40+1,73=3,13A.
Кирхгофтың бірінші заңы бойынша I4 тоғын анықтаймыз:
I 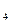 ’=I
’=I 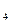 -J
-J 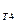 =-1,40-2= -3,4A.
=-1,40-2= -3,4A. 
1.3 теңдеулер жүйесі ЭВМ-де шығаруға болады, бұл жағдайда контурлық тоқтардың теңдеулерін матрицалық түрде жазу кажет:
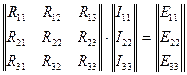
1.3 Түйіндік потенциалдар тәсілі бойынша электр тізбектің барлық тармақтарындағы тоқтарды есептеу.
(1.2-cурет) Электр тізбегі үшін түйіндік потенциалдарды анықтаймыз. Әрбір тармақтың өткізгіштіктерін есептейміз:
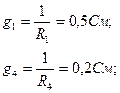
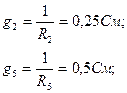
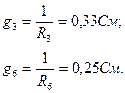
Кез-келген түйіннің потенциалын 0-ге теңестіреміз, 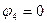 болсын.
болсын.
Түйіндік потенциалдарды анықтау үшін теңдеулер жазайық;
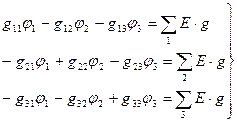 (1.5)
(1.5)
g 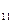 ,g
,g 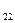 ,g
,g 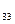 – меншікті түйіндік өткізгіштік – берілген түйінге қосылған тармақтардың өткізгіштіктерінің қосындысына тең.
– меншікті түйіндік өткізгіштік – берілген түйінге қосылған тармақтардың өткізгіштіктерінің қосындысына тең.
g 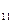 =g
=g 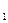 +g
+g 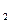 +g
+g 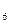 =1См;
=1См;
g 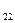 =g
=g 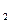 +g
+g 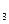 +g
+g 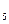 =1,08См;
=1,08См;
g 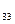 =g
=g 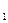 +g
+g 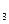 +g
+g 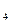 =1,03См.
=1,03См.
g 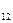 =g
=g 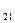 , g
, g 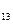 =g
=g 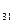 , g
, g 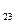 =g
=g 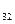 – жалпы түйіндік өткізгіштік – қарастырылатын түйіндерді өзара қосатын тармақтардың өткізгіштіктерінің қосындысына тең.
– жалпы түйіндік өткізгіштік – қарастырылатын түйіндерді өзара қосатын тармақтардың өткізгіштіктерінің қосындысына тең.
g 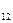 =g
=g 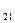 =g
=g 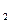 =0,25См;
=0,25См;
g 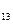 =g
=g 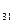 =g
=g 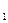 =0,5См;
=0,5См;
