Числовые последовательности. 1. Определение числовой последовательности

1. Определение числовой последовательности. Кванторы.Если каждому числу n из натурального ряда по некоторому закону поставлено в соответствие определенное действительное число 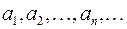, то говорят, что задана числовая последовательность. Числа 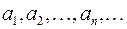называются членами или элементами последовательности, 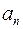называют общим членом последовательности. Последовательность обозначают так: .

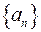Кванторами называются символы: 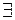- «существует», 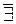- «не существует», 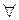- «любой».

2. Последовательности чисел. Предел последовательности.Занумерованное множество вещественных чисел называют последовательностью вещественных чисел. Обозначается последовательность

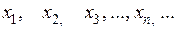
или коротко 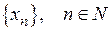. Число 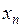называется членом (элементом) последовательности, 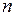- номером элемента последовательности.

Число 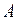называется пределом последовательности 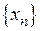, если 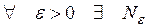такое, что 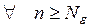выполнено 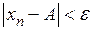. Обозначение:

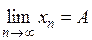(1)

Последовательность, имеющая предел называется сходящейся, а не имеющая предел – расходящийся. Последовательность 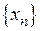называется ограниченной, если 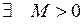такое, что .

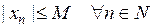Последовательность 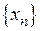называется неограниченной, если 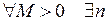такое, что

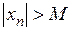(2)

Отсюда следует, что у неограниченных последовательностей бесконечно много элементов удовлетворяют условию неограниченности (2).

Сходящаяся последовательность имеет только один предел и является ограниченной.

Последовательность 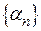называется бесконечно малой, если

.

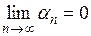Последовательность 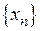называется бесконечно большой, если 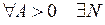такое, что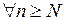

.

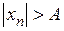Обозначение: .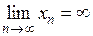

В этом случае говорят, что последовательность 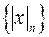имеет предел, равный .

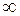Говорят, что последовательность 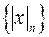имеет предел +∞ ( 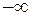), если ∀А>0 ∃ номер N, что 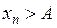( 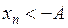) при 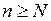, и обозначают:

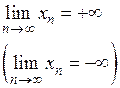
Заметим, что у бесконечно больших последовательностей предел не существует, символ 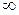является не числом, а формальным значком.

Справедливы следующие свойства последовательностей:

1. Сходящуюся последовательность можно представить в ви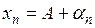де , где 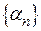- бесконечно малая последовательность, A- предел последовательности.

2. Сходящаяся последовательность является ограниченной.

3. Произведение и сумма бесконечно малых последовательностей есть бесконечно малая последовательность.

4. Произведение бесконечно больших последовательностей есть бесконечно большая последовательность.

5. Произведение ограниченной на бесконечно малую последовательность есть бесконечно малая последовательность.

6. Произведение сходящейся последовательности, предел которой не равен нулю, на бесконечно большую последовательность есть бесконечно (большая) последовательность.