Знакопеременные ряды.Абсолютная и условная сх-сть
Ряд называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные.
Теорема1. Если знакопеременный ряд 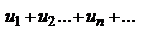 таков, что ряд, составленный из абсолютных величин его членов
таков, что ряд, составленный из абсолютных величин его членов 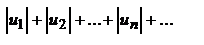 сходится, то и данный знакопеременный ряд также сходится.
сходится, то и данный знакопеременный ряд также сходится.
Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов. Если же знакопеременный ряд сходится, а ряд, составленный из абсолютных величин его членов расходится, то данный ряд называется условно или не абсолютно сходящимся рядом.
45.1.Вычисление объёмов тел по площадям параллельных сечений
Теорема. Объем тела с допустимыми параллельными сечениями вычисляется по формуле 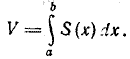 (1)
(1)
Отрезок [а; b] точками

разобьем на п отрезков [хi—1 ; хi] длины
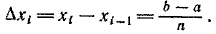
Пусть тi и Mi — наименьшее и наибольшее значения функции S(x) на отрезке
[хi—1 ; хi] .Плоскостями х = хi, где i = 1, 2, ..., п — 1, тело D разобьем на n слоев. Выделим i-й слой, соответствующий отрезку [хi—1 ; хi], и построим два цилиндра высрты Δхi :
один с основанием площади Mi , содержащий i-й слой, а другой с основанием площади тi , содержащийся в i-м слое (рис. 248).
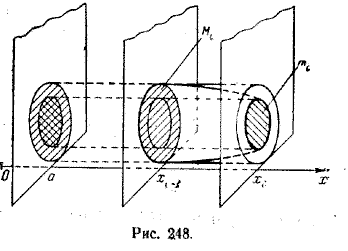
Объемы этих цилиндров равны Mi Δхi и тi Δхi.
Произведя указанные построения для каждого слоя, получим два ступенчатых тела D'n и D"n таких, что D'n < D < D''n. Их объемы равны
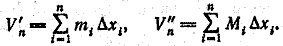
Так как функция S(x) непрерывна, то V'n и V"n при п —> ∞ имеют один и тот же предел, равный 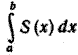 .Следовательно, объем тела D вычисляется по формуле (1).
.Следовательно, объем тела D вычисляется по формуле (1).
Интегральный признак сх-сти ряда.Ряд Дирихле.
80. Рядом Дирихле называется 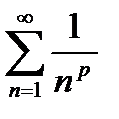 , где p – некоторые действительные числа. , где p – некоторые действительные числа. |
| Исследуем на сходимость этот ряд при помощи интегрального признака. Для этого рассмотрим несобственный интеграл. |
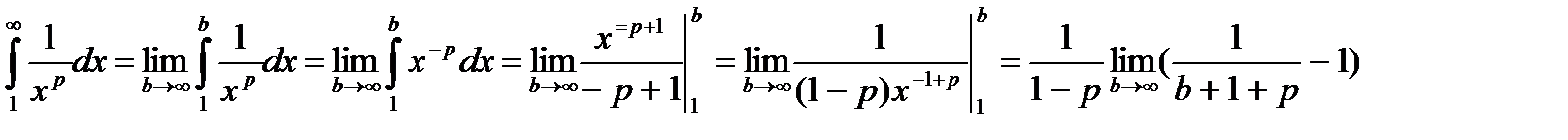 |
| при p<1 – сходится |
| при p>1 – расходится |
| p=1 |
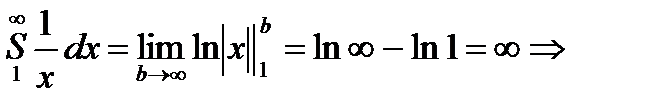 ряд расходится. ряд расходится. |
Т.о. ряд Дирихле 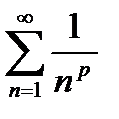 - сходится при p>1 и расходится при p<1 - сходится при p>1 и расходится при p<1 |
при 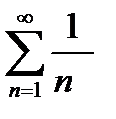 - гармонический ряд расходится. - гармонический ряд расходится. |
46.1.Приближённые вычисления опр-ных интегралов
