Глава 3. кривые второго порядка

Эллипс.

Определение. Эллипсом называется множество точек g на плоскости, обладающее следующим свойством: существуют такие точки F₁, F₂, называемые фокусами, что сумма расстояний от произвольной точки M эллипса до F₁ и от M до F₂ есть величина постоянная:

½ MF₁½ +½ MF₂½ = 2a = const, (1)

т.е. независящая от выбора точки MÎg, и 2a < 2c =½ F₁F₂½ .

Составим уравнение эллипса в декартовых координатах. Начало координат поместим в середину отрезка F₁F₂, и направим Ox­­. Тогда ось Oy определится однозначно. Фокусы будут иметь координаты F₁(c, 0), F₂(– c, 0).

Пусть M(x, y) – произвольная точка эллипса. Тогда

½ MF₁½ = , ½ MF₂½ = .

Согласно определению (1) имеем

= 2a – .

Возведем обе части равенства в квадрат и сократим одинаковые слагаемые:

x² – 2xc + c² + y² = 4a² – 4a + x² + 2xc + c² + y² .

4xc = 4a² – 4a Û a = a² + xc.

Еще раз возводим в квадрат, сокращаем и группируем:

a²(x² + 2xc + c² + y²) = a⁴ + 2a²xc + x²c²,

x²(a² – c²) + a²y² = a²(a² – c²).

Согласно определению a < c; поэтому можем обозначить b² = a² – c² , и разделив на a²b², окончательно получаем

+ = 1 . (2 )

Мы доказали, что координаты произвольной точки эллипса удовлетворяют уравнению (2). Необходимо еще доказать обратное: если координаты точки M(x, y) удовлетворяют (2), то выполнено (1).

Из (2) выразим y² = b²(1– ) и подставим в выражение для ½ MF₁½, учитывая при этом обозначение b² = a² – c²:

½ MF₁½ = = =

= =

= = =½ a – ½.

Аналогично получаем, что ½ MF₂½ =½a + ½. Из (2) следует, что ½ x ½ £ a (иначе уже первое слагаемое будет больше 1), а по определению, a < c Þ оба выражения под модулем неотрицательны. Поэтому

½ MF₁½ +½ MF₂½ = a – + a + = 2a.

Уравнение (2) называется каноническим уравнением эллипса.

Геометрические свойства эллипса.

1. Из (2) следует, что ½ x ½ £ a, ½ y ½ £ b. Значит, эллипс целиком содержится в прямоугольнике, определяемыми этим неравенствами.

Подчеркнем, что это и все другие свойства выводятся только из уравнения эллипса, без ссылки на наглядность чертежа. Поэтому и раздел геометрии, который мы сейчас изучаем, называется «Аналитическая геометрия».

2. Координатные оси пересекают эллипс в точках A₁(a, 0), A₂(– a, 0), B₁(0, b), B₂(0, – b), которые называются его вершинами. Отрезки A₁A₂ и B₁B₂ называются большим и малым диаметрами эллипса, а вместе – главными диаметрами. Числа a и b называются большой и малой полуосями.

3. Координатные оси являются осями симметрии эллипса, а начало координат – центром симметрии.

Действительно, пусть M(x, y) – произвольная точка эллипса. Тогда

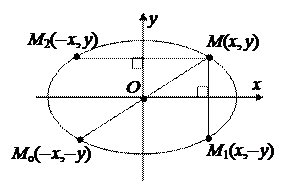пара (x, y) удовлетворяет уравнению (2). Но тогда этому уравнению удовлетворяют также и пары (x, – y), (– x, y), (– x,– y), которые задают точки, симметричные M относительно Ox, Oy и точки O соответственно.

4. Эллипс может быть получен из окружности

g¢: X ² + Y ² = a² (**)

в результате равномерного ее сжатия вдоль оси Oy с коэффициентом k = a/b. Действительно, при таком сжатии точка M ¢(X, Y)Î g¢ будет переходить в точку M(x, y), где

x = X , X = x ,

y = Y . Û Y = y .

Подставляя последние формулы в (**), получим, что координаты точки M удовлетворяют (2), т.е. MÎ g .

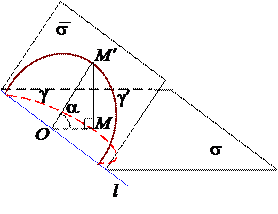5. Эллипс может быть получен из окружности в результате проекции окружности на плоскость s непараллельную плоскости окружности . Действительно, при такой проекции отрезки параллельные линии пересечения плоскостей l = s I сохраняют длину, а отрезки перпендикулярные l сжимаются в 1/cos a раз, где a – угол между s и . Таким образом, окружность сжимается по одному направлению, и согласно свойству 4, из нее получается эллипс.

6.Самостоятельно убедитесь, что параметрические уравнения эллипса имеют вид:

x = a cos a ,

y = b sin a , t ÎR .

Гипербола.

Определение. Гиперболой называется множество точек g на плоскости, обладающее следующим свойством: существуют такие точки F₁, F₂, называемые фокусами, что модуль разности расстояний от произвольной точки M гиперболы до F₁ и от M до F₂ есть величина постоянная:

½ ½ MF₁½ –½ MF₂½½ = 2a = const, (3)

т.е. независящая от выбора точки MÎg, и 2a < 2c =½ F₁F₂½ .

Составим уравнение гиперболы в декартовых координатах. Начало координат поместим в середину отрезка F₁F₂, 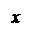и направим Ox­­. Тогда ось Oy определится однозначно. Фокусы будут иметь координаты F₁(c, 0), F₂(– c, 0).

Пусть M(x, y) – произвольная точка гиперболы. Тогда

½ MF₁½ = ,

½ MF₂½ = .

Согласно определению (3) имеем

= ± 2a + .

Далее совершаем дословно такие же преобразования, что и для эллипса. В результате получим уравнение

x²(c² – a²) – a²y² = a²(c² – a²).

Упражнение. Проделайте эти преобразования самостоятельно.

По определению a < c; поэтому можем обозначить b² = c² – a², и разделив на a²b² окончательно получаем

– = 1 . (4 )

Мы доказали, что координаты произвольной точки гиперболы удовлетворяют (4). Необходимо еще доказать обратное: если координаты точки M(x, y) удовлетворяют (4), то выполнено (3). Из (4) выразим y² = b²( –1) и подставим в выражение для ½ MF₁½, учитывая при этом обозначение b² = c² – a². Точно так же, как и для эллипса получим

½ MF₁½ =½ a – ½, ½ MF₂½ ==½ a + ½. (**)

Упражнение. Проделайте это самостоятельно.

Из (4) вытекает, что x² = a²(1+ ) Þ ½ x ½ ³ a, и по определению c > a. Значит, второе слагаемое в формулах (**) по модулю больше первого и при x ³ a получаем

½ MF₁½ = – a, ½ MF₂½ = a + ,

а при x £– a получаем

½ MF₁½ = a – , ½ MF₂½ = – a – .

В обоих случаях выполняется (3).

Уравнение (4) называется каноническим уравнением гиперболы.

Геометрические свойства гиперболы.

1. Мы уже отмечали, что для любой точки M(x, y) на гиперболе

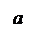
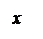
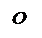
x² = a²(1+ ) Þ ½ x ½ ³ a,

кроме того (4 ) Þ

x² > Û ½ x ½>½ y ½.

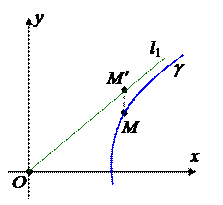
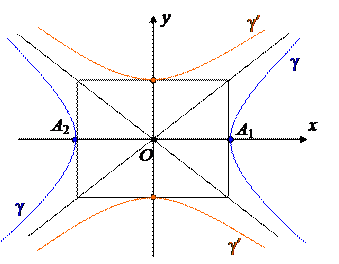
Значит вся гипербола содержится в области, определяемой этими неравенствами. Она заштрихована на рисунке.

2.Ось Ox пересекает гиперболу в точках A₁(a, 0), A₂(– a, 0),которые называются вершинами гиперболы. Ось Oy ее не пересекает. Числа a и b называются полуосями гиперболы – действительной и мнимой.

3. Дословно так же, как и для эллипса доказывается, что координатные оси являются осями симметрии эллипса, а начало координат – центром симметрии.

4.Прямые l₁: y = x и l₂: y = – x называются асимптотами гиперболы.

Гипербола неограниченно к ним приближается, но нигде не пересекает.

Действительно, пусть M(x, y) – точка на гиперболе, а M ¢(x, y ¢) – на соответствующей асимптоте. Тогда расстояние от точки M до асимптоты меньше, чем ½ MM ¢½. При этом

½ MM ¢½ =½ y ¢½ –½ y½ .

(y ¢)²= x², y² = b²( –1) (*** )

Из этих равенств вытекает, что при ½ x ½¾®¥ будет ½ y ¢½ ¾®¥ и ½ y½ ®¥ . Кроме этого,

(y ¢)²– y² = b² Û ½ y ¢½ –½ y½ = ¾®0 при ½ x ½¾®¥.

Заметим, что обе асимптоты вместе можно задать вместе одним уравнением – = 0 . Для его получения достаточно в правой части уравнения (4) заменить 1 на 0. Асимптоты проходят через диагонали прямоугольника, который определяется неравенствами ½ x ½ £ a, ½ y ½ £ b. Он называется фундаментальным прямоугольником гиперболы. Для построения гиперболы рекомендуется сначала изобразить этот прямоугольник.

5. При a = b гипербола называется равнобокой. Ее уравнение

x²– y² = a² , (5)

а асимптоты имеют уравнения l₁: y = x , l₂: y = – x . Очевидно, что l₁ ^ l₂ , и мы можем выбрать их за оси новой декартовой СК Ox ¢y ¢, которая получается из Oxy поворотом на угол – 45^о. Тогда формулы замены координат имеют вид:

x = ( x ¢+ y ¢) ,

y = (– x ¢+ y ¢).

Подставим их в (5) и получим уравнение

2x ¢y ¢= a² Û y ¢= ,

где k = a²/2. Таким образом, равнобокая гипербола задает график обратной пропорциональности.

6. Параметрические уравнения гиперболы имеют вид:

x = ± ach t , x = a(t + 1/t),

y = bsh t, t ÎR . y = b(t – 1/t), t ÎR\{0}.

Знак «+» соответствует одной ветви гиперболы, а «–» – другой ветви.

Упражнение. Проверьте это самостоятельно.

7. Гипербола

g¢: – = –1 ,

называется сопряженной к гиперболе g, заданной уравнением (4). Она имеет тот же фундаментальный прямоугольник, те же асимптоты, только расположена в другой паре вертикальных углов, образованных этими асимптотами.